Why Does a Code Submission Timeout After Submission? How Large is n for O(n) Algorithms to Timeout?

Some students may not have a clear understanding of how fast a computer can execute operations. They might think that computers run at an incredibly fast pace. So, why do algorithms on LeetCode timeout?

How many operations can a computer execute in 1 second? Let's explore this question.

What Does Timeout Mean?

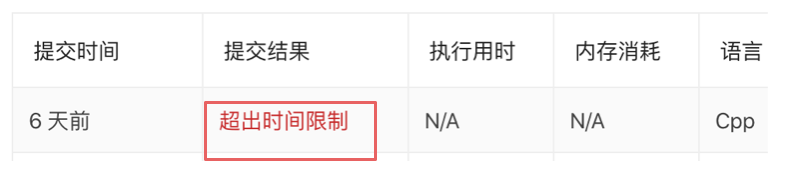
When practicing algorithms on LeetCode, you might have encountered an error called "timeout."

This means the program's execution time has exceeded the allowed time limit. Generally, the time limit for OJ (online judge) is 1 second, which means the input data must produce a result within 1 second after being entered. Although we are not entirely sure of LeetCode's evaluation rules, for convenience, let's assume the timeout limit is 1 second.

If you have written an O(n) algorithm, you can estimate the value of n when the algorithm's execution time will exceed 1 second.

When n reaches a scale whereby an O(n) algorithm takes more than 1 second to execute, you should consider a log(n) solution.

Understanding Computer Performance Through Hardware

The speed of a computer primarily depends on the CPU configuration. Take the 2015 MacPro as an example, with CPU specifications: 2.7 GHz Dual-Core Intel Core i5.

This means a 2.7 GHz dual-core, i5 processor. What does GHz mean? 1Hz = 1/s; 1Hz refers to a CPU pulse (understood as a state change, also known as a clock cycle), known as hertz. So, how many hertz does 1GHz equal?

• 1GHz (gigahertz) = 1000MHz (megahertz)
• 1MHz (megahertz) = 1 million hertz

Thus, 1GHz = 1 billion Hz signifies that the CPU can pulse 1 billion times per second (1 billion clock cycles). Note that a single clock cycle does not equate to a single CPU operation.

For example, the operation 1 + 2 = 3 requires four steps: step one: putting 1 into a register, step two: putting 2 into a register, step three: performing the addition, and step four: saving the result.

Furthermore, the CPU isn't dedicated solely to running our program; it also executes various processes and tasks on the computer. Our program is merely one among many.

So, how many operations can our program genuinely execute in 1 second on the computer?

Conducting a Test Experiment

When writing a test program to measure how large the data scale can be processed in 1 second, keep three points in mind:

• The time a CPU takes to execute each instruction can vary; for example, it may take different amounts of time for addition and multiplication operations.
• Most modern computer systems have cache techniques, so frequent access of the same address and accessing non-adjacent elements require different amounts of time.
• The computer runs multiple programs simultaneously, with different processes and threads competing for resources within each program.

Despite these factors, you can have a good estimation of your program's runtime.

A quote from "Algorithms, 4th Edition" states:

• Rocket scientists will need to know if a test rocket is going to land in the ocean or in a city;
• Medical researchers need to know if a drug test will kill or cure the subject;

So, any software engineer developing on computers should roughly estimate if a program will run for one second or one year.

This is fundamental, so those discrepancies are not a concern.

Below is a C++ code example:

Testing hardware: 2015 MacPro, CPU configuration: 2.7 GHz Dual-Core Intel Core i5

Implement three functions with time complexities of O(n), O(n^2), and O(n log n), using addition operations for uniform testing.

// O(n)
void function1(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        k++;
    }
}

// O(n^2)
void function2(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long j = 0; j < n; j++) {
            k++;
        }
    }
}

// O(n log n)
void function3(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long long j = 1; j < n; j = j*2) { // Note here j=1
            k++;
        }
    }
}

Let's see how the execution time changes with the scale of n for these three functions. First, test function1 by commenting out function2 and function3.

int main() {
    long long n; // Data scale
    while (1) {
        cout << "Enter n: ";
        cin >> n;
        milliseconds start_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
        );
        function1(n);
//        function2(n);
//        function3(n);
        milliseconds end_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
        );
        cout << "Time elapsed: " << milliseconds(end_time).count() - milliseconds(start_time).count()
            <<" ms"<< endl;
    }
}

The running result is shown below:

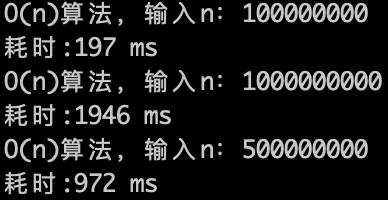
For an O(n) algorithm, the computer can perform approximately 5 * (10^8) calculations in 1 second. We can infer that for an O(n^2) algorithm, it can handle about the square root of 5 * (10^8) within 1 second. The experimental data is shown below.

For an O(n^2) algorithm, it performs around 22,500 calculations in 1 second, confirming our inference.

Now, let's speculate about the data scale for O(n log n), what can 1 second handle?

Theoretically, it should be one order of magnitude less than O(n) because log(n) complexity is quite fast, as seen in the experimental data.

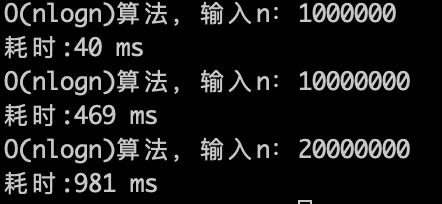
With an O(n log n) algorithm, a computer can perform approximately 2 * (10^7) calculations in 1 second, which matches expectations.

These are my personal PC's measured data, it's not entirely precise but the order of magnitude is similar. You can measure your computer and compare the results.

Summary of Test Data:

For time complexities such as O(log n) and O(n^3), you can write some code to test the scale of data they can handle within 1 second.

Complete Test Code

#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
// O(n)
void function1(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        k++;
    }
}

// O(n^2)
void function2(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long j = 0; j < n; j++) {
            k++;
        }
    }

}
// O(nlogn)
void function3(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long long j = 1; j < n; j = j*2) { // Note here j=1
            k++;
        }
    }
}
int main() {
    long long n; // Data scale
    while (1) {
        cout << "Enter n: ";
        cin >> n;
        milliseconds start_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
        );
        function1(n);
//        function2(n);
//        function3(n);
        milliseconds end_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
        );
        cout << "Time elapsed: " << milliseconds(end_time).count() - milliseconds(start_time).count()
            <<" ms"<< endl;
    }
}

Summary

This article thoroughly analyzes why code submissions might timeout during LeetCode challenges, evaluates CPU execution speeds through hardware configuration, and demonstrates an experiment to determine how large n can be for an O(n) algorithm to execute within one second. It also provides the data size that different time complexities can handle in one second.

It's recommended that fellow developers also conduct similar experiments to see if their results are comparable to mine.

With this, everyone should have a better understanding of the data scale when a program times out.