Dynamic Programming: 0-1 Knapsack Theoretical Basics (Rolling Array)

This problem does not have an exact counterpart on LeetCode, but you can practice on KamaCoder Problem 46 (opens new window).

Approach

In yesterday's article, Dynamic Programming: The Basics of 0-1 Knapsack (opens new window), a two-dimensional dp array was used to explain the 0-1 knapsack problem.

Today, we will discuss the rolling array. In fact, we have already used rolling arrays in previous problems by reducing the two-dimensional dp array to a one-dimensional dp array. Some readers expressed confusion at the time.

Let's thoroughly discuss rolling arrays through the 0-1 knapsack problem!

We will use the following example for illustration:

The maximum weight capacity of the knapsack is 4.

The items are:

	Weight	Value
Item 0	1	15
Item 1	3	20
Item 2	4	30

What is the maximum value that the knapsack can carry?

One-dimensional dp Array (Rolling Array)

The states in knapsack problems can indeed be compressed.

When using a two-dimensional array, the recurrence relation is: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

We can see that if we copy the layer dp[i - 1] onto dp[i], the expression can be simplified to: dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

Instead of copying the dp[i - 1] layer to dp[i], we can use a one-dimensional array, considered as a rolling array.

This is the origin of the rolling array, where the previous layer can be reused, directly copied to the current layer.

By this point, you might have forgotten what i and j in dp[i][j] represent; i refers to items, and j refers to knapsack capacity.

dp[i][j] represents the maximum value obtainable by selecting from items indexed from [0-i] to fill a knapsack with capacity j.

It is essential to remember what i and j mean, otherwise, it will be easy to get confused.

The five-step dynamic programming analysis is as follows:

1. Define the dp Array

The definition of the dp array is explained in detail in Partition Equal Subset Sum (opens new window).

In the one-dimensional dp array, dp[j] represents the maximum value that can be carried within a knapsack with capacity j.

2. Recurrence Relation for One-dimensional dp Array

The recurrence relation for a two-dimensional dp array is: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

How this relation comes about is explained in detail in Partition Equal Subset Sum (opens new window).

For the one-dimensional dp array, we essentially copy the previous layer dp[i-1] to the current layer dp[i].

So, based on the aforementioned recurrence relation, we can drop the i dimension.

The recurrence relation becomes: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

The analysis is as follows:

dp[j] denotes the maximum value a knapsack with capacity j can carry.

dp[j] can be derived from dp[j - weight[i]], where dp[j - weight[i]] refers to the maximum value a knapsack with capacity j - weight[i] can carry.

dp[j - weight[i]] + value[i] represents the value when adding item i to a knapsack with capacity [j - weight[i]] (i.e., the value of dp[j] after item i is added).

Here, dp[j] has two choices: either maintaining its own value dp[j] (as in the two-dimensional dp array's dp[i-1][j], meaning item i is not added) or taking dp[j - weight[i]] + value[i] (adding item i). It seeks the maximum value since the aim is to maximize the value.

The recurrence relation is thus:

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

Here, the i dimension of the two-dimensional dp array writing is removed.

3. Initialization of the One-dimensional dp Array

Initialization must align with the dp array definition; otherwise, it becomes increasingly convoluted during recurrence.

dp[j] represents the maximum value for a knapsack of capacity j. Hence, dp[0] should be 0 since a knapsack with zero capacity holds zero value.

Beyond index 0, how do we initialize other indexes in the dp array?

Looking at the recurrence relation: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

During the dp array derivation, the task is to select the maximum value. If all item values are positive integers, then non-zero indices can be initialized to 0.

This ensures that during the recurrence process, the dp array captures the maximum value, not overridden by initial values.

Assuming item values are greater than zero, merely initializing the dp array to 0 suffices.

4. Iteration Order of the One-dimensional dp Array

Here's the code:

for(int i = 0; i < weight.size(); i++) {  // Iterate through items
    for(int j = bagWeight; j >= weight[i]; j--) {  // Iterate through knapsack capacity
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

You may notice that the order of iterating knapsack capacities differs from that in the two-dimensional dp version!

In a two-dimensional dp, the knapsack capacity is iterated from small to large, whereas in one-dimensional dp, it is iterated from large to small.

Why?

Iterating in reverse order ensures that each item i is only added once! If iterated in a forward order, item 0 could be added multiple times!

For example: Item 0 weighs weight[0] = 1 with a value of value[0] = 15.

If iterated forward:

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

Now dp[2] is already 30, meaning item 0 was added twice, thus forward iteration won't work.

Why does reverse iteration guarantee that each item is added only once?

Reverse iteration calculates dp[2] first:

dp[2] = dp[2 - weight[0]] + value[0] = 15 (Assuming dp array is initialized to 0)

dp[1] = dp[1 - weight[0]] + value[0] = 15

In backward iteration, each state retrieved doesn't overlap with past states, ensuring each item is included only once.

Why doesn't the two-dimensional dp array require reverse iteration?

Because in a two-dimensional dp, dp[i][j] is calculated based on the previous layer dp[i - 1][j], so the current layer dp[i][j] will not be overridden!

(If this doesn't make sense, it’s recommended to try it out — contemplation alone can be misleading, while experience brings knowledge!)

Can the order of the two nested for-loops be swapped — can we iterate knapsack capacities in the outer loop and items in the inner loop?

No!

In a one-dimensional dp array setup, the knapsack capacity must be iterated in reverse order (as previously explained). If knapsack capacities are iterated in the outer loop, each dp[j] will accommodate only one item, meaning the knapsack will hold only one item.

The traversal order for one-dimensional dp arrays significantly differs from that of two-dimensional arrays! This is crucial to understand.

5. Example Walkthrough of the dp Array

In a one-dimensional dp, by iterating through the knapsack with items 0, 1, and 2 respectively, the final result is:

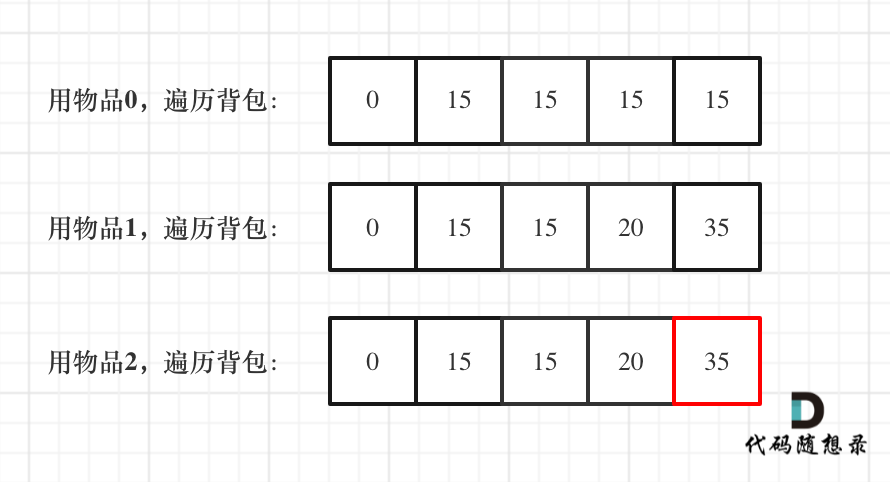
This problem doesn’t have an exact counterpart on LeetCode but can be practiced on KamaCoder Problem 46 (opens new window), with the same intent. The code is as follows:

// One-dimensional dp array implementation
#include <iostream>
#include <vector>
using namespace std;

int main() {
    // Read M and N
    int M, N;
    cin >> M >> N;

    vector<int> costs(M);
    vector<int> values(M);

    for (int i = 0; i < M; i++) {
        cin >> costs[i];
    }
    for (int j = 0; j < M; j++) {
        cin >> values[j];
    }

    // Create a dynamic programming array dp, initialized to 0
    vector<int> dp(N + 1, 0);

    // Outer loop iterates over each type of research material
    for (int i = 0; i < M; ++i) {
        // Inner loop decreases from N capacity down to the current research material’s occupied capacity
        for (int j = N; j >= costs[i]; --j) {
            // Consider the case of selecting and not selecting the current research material, selecting the maximum value
            dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
        }
    }

    // Output dp[N], the maximum value of research materials that can be carried in the given N luggage capacity
    cout << dp[N] << endl;

    return 0;
}

A one-dimensional dp for the 0-1 knapsack is significantly more concise than a two-dimensional one, simplifying both initialization and iteration order.

I prefer using a one-dimensional dp array because it’s more intuitive, concise, and reduces space complexity by an order of magnitude!

For future discussions on knapsack problems, the intonation will directly employ a one-dimensional dp array for derivation.

Summary

An interview question can be derived from this discussion (since LeetCode doesn't have the original problem).

The question would require implementing a purely two-dimensional 0-1 knapsack. If this is achieved, further ask why the nested for-loop order is such. Can it be reversed? Elaborate on the initialization logic.

Then, implement a one-dimensional array for the 0-1 knapsack, and ask: Can the order of the two nested for-loops in a one-dimensional array be reversed? Why?

The above questions assume the candidate has already written out the code.

It is evident just from a purely 0-1 knapsack problem whether a candidate truly understands the algorithm — no need to test more applied classes of knapsack problems.

Readers who have gone through this article should easily have the answers to the questions above!

This concludes the foundational theory behind the 0-1 knapsack problem. I spent two articles dissecting every aspect of the dp array definitions, recurrence formulas, initialization, iteration order from two-dimensional to one-dimensional arrays, leaving no difficult point uncovered.

The articles are quite information-rich.

If you've grasped the content of both Dynamic Programming: The Basics of 0-1 Knapsack (opens new window) and this current article, subsequent 0-1 knapsack problems will appear much simpler.

Instead of relying solely on intuition or rote memory, you'll apply your own understanding, appreciating the underlying essence, with code fully under your control.

Even if the code doesn't pass, you'll have your own logical structure for debugging, leading to clearer thinking.

Other Language Versions

Java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // Read M and N
        int M = scanner.nextInt();  // Number of research materials
        int N = scanner.nextInt();  // Size of the luggage space

        int[] costs = new int[M];   // Space occupied by each material
        int[] values = new int[M];  // Value of each material

        // Input space occupation of each material
        for (int i = 0; i < M; i++) {
            costs[i] = scanner.nextInt();
        }

        // Input value of each material
        for (int j = 0; j < M; j++) {
            values[j] = scanner.nextInt();
        }

        // Create a dynamic programming array dp, initially set to 0
        int[] dp = new int[N + 1];

        // Outer loop iterates over each type of research material
        for (int i = 0; i < M; i++) {
            // Inner loop decreases from N capacity down to the current research material’s occupied capacity
            for (int j = N; j >= costs[i]; j--) {
                // Consider the current research material's selection and non-selection cases, choose the maximum value
                dp[j] = Math.max(dp[j], dp[j - costs[i]] + values[i]);
            }
        }

        // Output dp[N], that is, the maximum value of research materials that can be carried in the given N luggage space
        System.out.println(dp[N]);

        scanner.close();
    }
}

Python

n, bagweight = map(int, input().split())
weight = list(map(int, input().split()))
value = list(map(int, input().split()))

dp = [0] * (bagweight + 1)  # Create a dynamic programming array dp, initially set to 0

dp[0] = 0  # Initialize dp[0] = 0, maximum value for knapsack with 0 capacity

for i in range(n):  # Iterate items first; if knapsack capacity is outer, each dp[j] will only accommodate one item
    for j in range(bagweight, weight[i]-1, -1):  # Backward iteration of knapsack capacity ensures each item i is used once
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

print(dp[bagweight])

Go

package main

import (
    "fmt"
)

func main() {
    // Read M and N
    var M, N int
    fmt.Scan(&M, &N)

    costs := make([]int, M)
    values := make([]int, M)

    for i := 0; i < M; i++ {
        fmt.Scan(&costs[i])
    }
    for j := 0; j < M; j++ {
        fmt.Scan(&values[j])
    }

    // Create a dynamic programming array dp, initially set to 0
    dp := make([]int, N + 1)

    // Outer loop iterates over each type of research material
    for i := 0; i < M; i++ {
        // Inner loop decreases from N capacity down to the current research material’s occupied capacity
        for j := N; j >= costs[i]; j-- {
            // Consider the current research material's selection and non-selection cases, choose the maximum value
            dp[j] = max(dp[j], dp[j-costs[i]] + values[i])
        }
    }

    // Output dp[N], that is, the maximum value of research materials that can be carried in the given N luggage space
    fmt.Println(dp[N])
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

JavaScript

const readline = require('readline').createInterface({
    input: process.stdin,
    output: process.stdout
});

let input = [];

readline.on('line', (line) => {
    input.push(line);
});

readline.on('close', () => {
    let [n, bagweight] = input[0].split(' ').map(Number);
    let weight = input[1].split(' ').map(Number);
    let value = input[2].split(' ').map(Number);

    let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));

    for (let j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for (let i = 1; i < n; i++) {
        for (let j = 0; j <= bagweight; j++) {
            if (j < weight[i]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

    console.log(dp[n - 1][bagweight]);
});

C

#include <stdio.h>
#include <stdlib.h>

int max(int a, int b) {
    return a > b ? a : b;
}

int main() {
    int n, bagweight;
    scanf("%d %d", &n, &bagweight);

    int *weight = (int *)malloc(n * sizeof(int));
    int *value = (int *)malloc(n * sizeof(int));

    for (int i = 0; i < n; ++i) {
        scanf("%d", &weight[i]);
    }
    for (int j = 0; j < n; ++j) {
        scanf("%d", &value[j]);
    }

    int **dp = (int **)malloc(n * sizeof(int *));
    for (int i = 0; i < n; ++i) {
        dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
        for (int j = 0; j <= bagweight; ++j) {
            dp[i][j] = 0;
        }
    }

    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for (int i = 1; i < n; i++) {
        for (int j = 0; j <= bagweight; j++) {
            if (j < weight[i]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

    printf("%d\n", dp[n - 1][bagweight]);

    for (int i = 0; i < n; ++i) {
        free(dp[i]);
    }
    free(dp);
    free(weight);
    free(value);

    return 0;
}