# Heard that the Knapsack Problem is Difficult? This Summary is Here to Save You

Before the end of the year, we covered all the aspects of the knapsack problem. Now it's time to summarize the knapsack problem comprehensively.

The knapsack problem is a very important part of dynamic programming, so I will separate it for a detailed summary. Once we've finished the dynamic programming section, we'll do an overall review of dynamic programming.

The relationship between these common knapsack problems is depicted as follows:

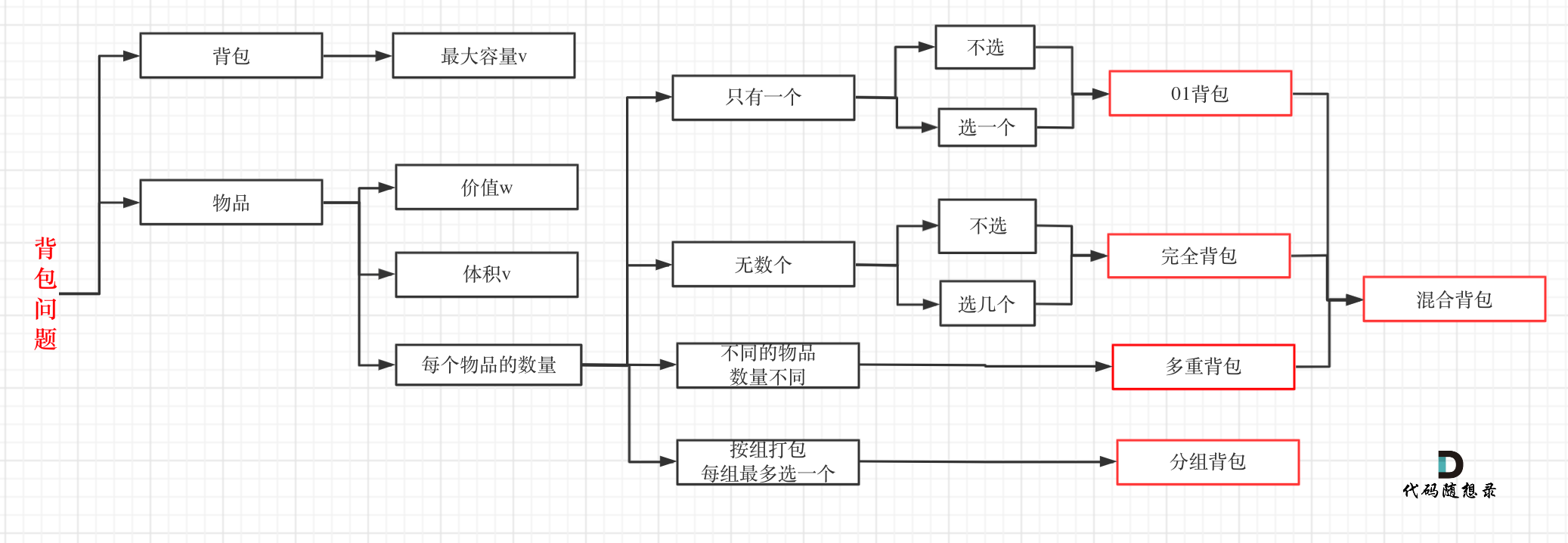
416.Partition Equal Subset Sum1

This diagram clearly distinguishes the relationships among these common knapsack problems.

When explaining the knapsack problem, we followed these five steps to gradually analyze it. As many of you may have experienced, understanding these five steps thoroughly can lead to a deeper understanding of dynamic programming.

Determine the dp array (dp table) and the meaning of its indices
Determine the state transition formula
How to initialize the dp array
Determine the iteration order
Derive the dp array with examples

Each of these five steps is critical, but determining the state transition formula and iteration order have regularity and representativeness, so I will summarize the knapsack problem mainly from these two points below.

# Knapsack State Transition Formula

Question: Can the knapsack be fully packed (or what is the maximum that can be packed)? Formula: dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);. Related problems:

Question: How many ways to fill the knapsack? Formula: dp[j] += dp[j - nums[i]]. Related problems:

Question: What is the maximum value that can fill the knapsack? Formula: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);. Related problems:

Dynamic Programming: 0474.Ones and Zeroes (opens new window)

Question: What is the minimum number of items needed to fill the knapsack? Formula: dp[j] = min(dp[j - coins[i]] + 1, dp[j]);. Related problems:

# Iteration Order

# 01 Knapsack

In Partition Equal Subset Sum (opens new window), we discussed that in a two-dimensional dp array implementation of the 01 knapsack, either iterating over items first or iterating over the knapsack capacity first works, and the second loop is from small to large.

And in Backpack Theory 01 Knapsack-2 (opens new window), we discussed that for a one-dimensional dp array implementation of the 01 knapsack, the items must be iterated over first, followed by the knapsack capacity, and the second loop is from large to small.

The iteration order in a one-dimensional dp array differs significantly from the two-dimensional dp array implementation of the 01 knapsack, so take note!

# Complete Knapsack

After discussing the 01 knapsack, let's look at the complete knapsack.

In Knapsack Problem Theory Basics Complete Knapsack (opens new window), we explained a pure one-dimensional dp array implementation of the complete knapsack, where both iterating over items first and iterating over the knapsack first works, and the second loop is from small to large.

However, this is only true for a pure complete knapsack. If the problem varies slightly, the order of the two for loops will change.

To calculate combinations, the outer for loop iterates over items, and the inner for loop iterates over the knapsack.

To calculate permutations, the outer for loop iterates over the knapsack, and the inner for loop iterates over items.

Relevant problems:

To calculate combinations: Dynamic Programming: 0518.Coin Change II (opens new window)
To calculate permutations: Dynamic Programming: 0377.Combination Sum IV (opens new window), Dynamic Programming: 0070.Climbing Stairs Complete Knapsack Version (opens new window)

If calculating the minimum number, the order of the two for loops does not matter. Relevant problems:

To calculate the minimum number: Dynamic Programming: 0322.Coin Change (opens new window), Dynamic Programming: 0279.Perfect Squares (opens new window)

For the knapsack problem, the state transition formula is relatively easy, but the iteration order is the challenging part. Understanding the iteration order thoroughly indicates a true grasp of the problem.

# Summary

This summary of the knapsack problem provides a high-level overview, focusing on the most critical two steps: the state transition formula and iteration order, abstracting from all related LeetCode problems.

In addition, each point is paired with corresponding LeetCode problems.

Lastly, if you want to learn about the multiple knapsack problem, see Knapsack Problem Theory Basics - Multiple Knapsack (opens new window). Currently, there are no LeetCode problems on multiple knapsack, nor is it a major focus during interviews.

Mastering the content I’ve summarized here will provide you with a deep understanding of the knapsack problem, which will be more than sufficient for tackling knapsack problems in interviews!

Knapsack problem summary:

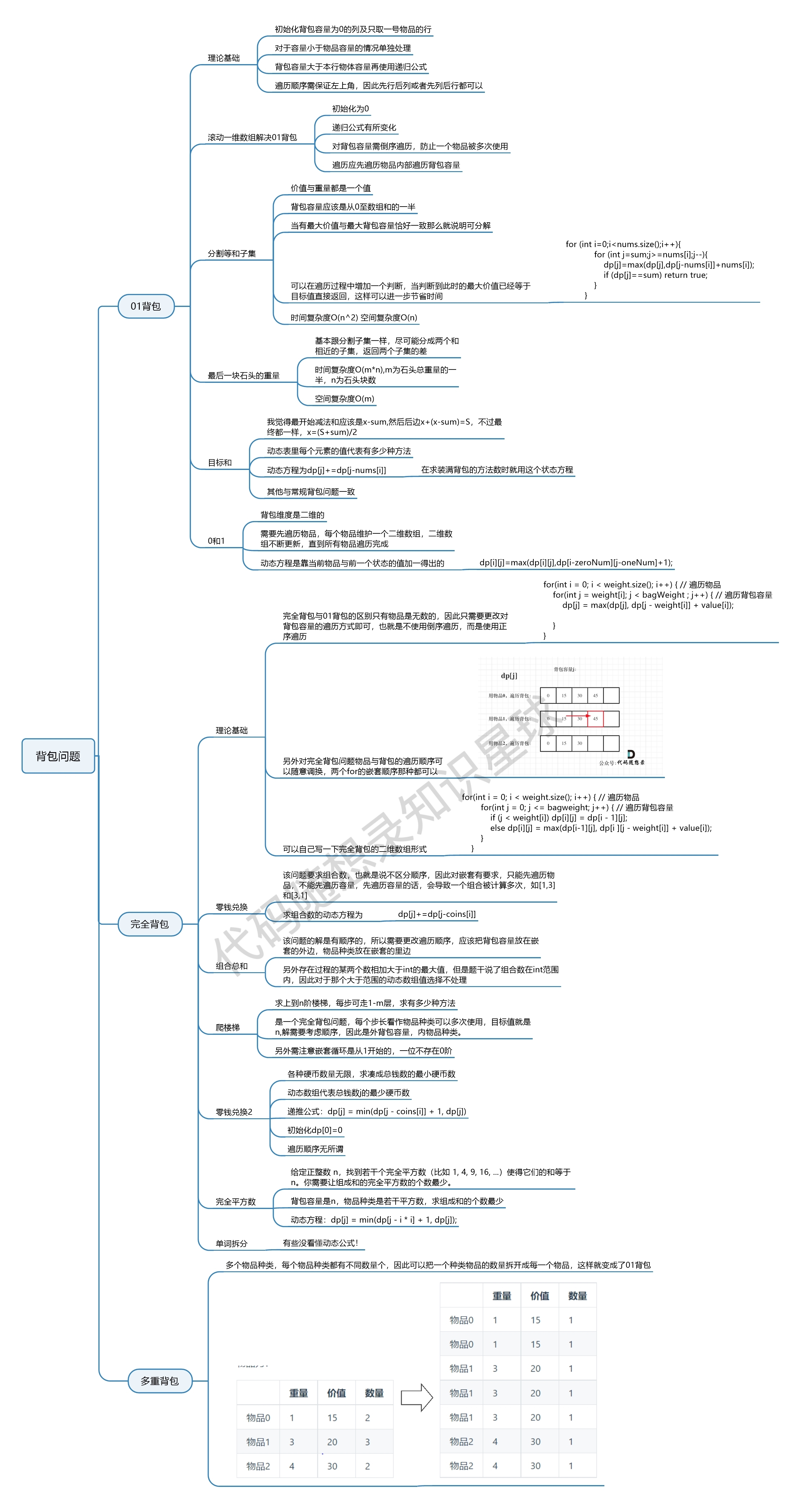
This diagram was excellently drawn and shared by a member named 海螺人 (opens new window) from the Keetcoder Knowledge Circle (opens new window).