Right Rotate a String

LeetCode has taken down the "Sword Offer" problems, so we provide similar problems on Kstar for practice.

Kstar Problem Link (opens new window)

The right rotation operation on a string involves moving several characters from the end of the string to the front. Given a string s and a positive integer k, write a function to move the last k characters to the front of the string, achieving a right rotation.

For example, given the input string "abcdefg" and integer 2, the function should convert it to "fgabcde".

Input:
The input consists of two lines. The first line contains a positive integer k, representing the number of positions to right rotate. The second line contains the string s, representing the string to be rotated.

Output:
The output is a single line, which is the string after the right rotation operation.

Sample Input:

2
abcdefg 

Sample Output:

fgabcde

Data Range: 1 <= k < 10000, 1 <= s.length < 10000

Approach

To make this problem more interesting and challenging: you cannot use extra space and must manipulate the string in place. (Note: Since Java does not allow modification of strings directly, you must allocate new space when using Java.)

With the restriction of not using extra space, it becomes quite challenging to simulate in-place operations to achieve the right rotation of the string.

In a previous problem 0151.Reverse Words in a String (opens new window), we discussed using a combination of global reversal and local reversal to reverse the order of words.

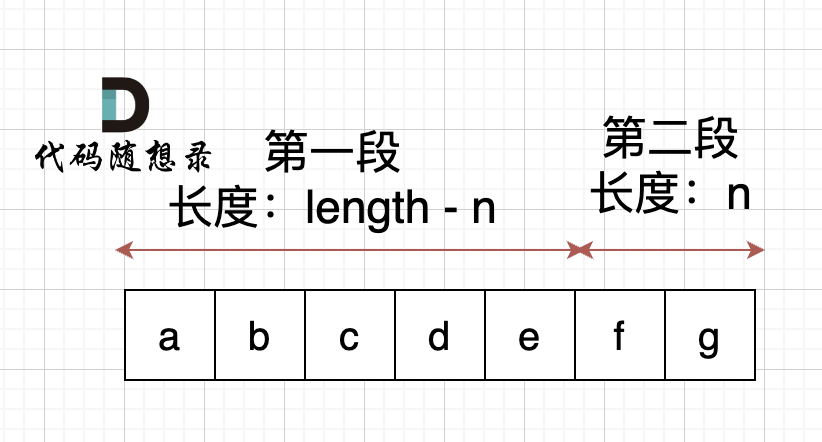
In this problem, we need to move the string right by n positions, effectively splitting the string into two parts. If n is 2, the string can be seen as divided into two parts, as shown in the illustration below: (length represents the length of the string)

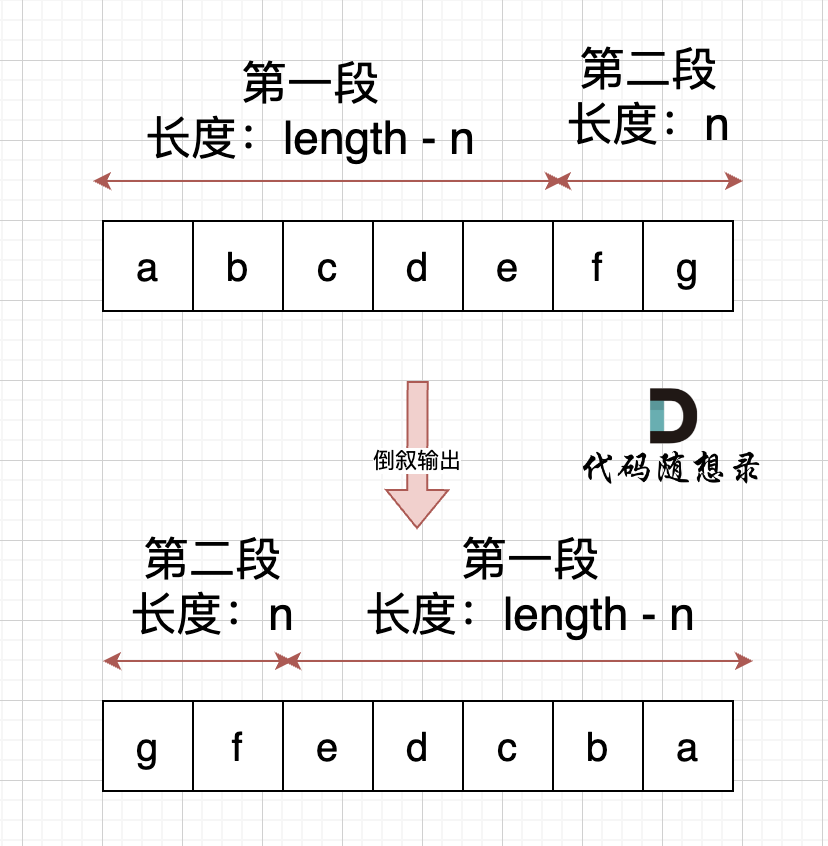
Right shifting by n positions involves placing the second segment before the first one, regardless of the order of characters within them. Isn't it possible to achieve this through global reversal, as shown below?

Now the first and second segments are in the desired order, but the characters within have been reversed. We need to reverse the characters within each segment, thereby correcting their order:

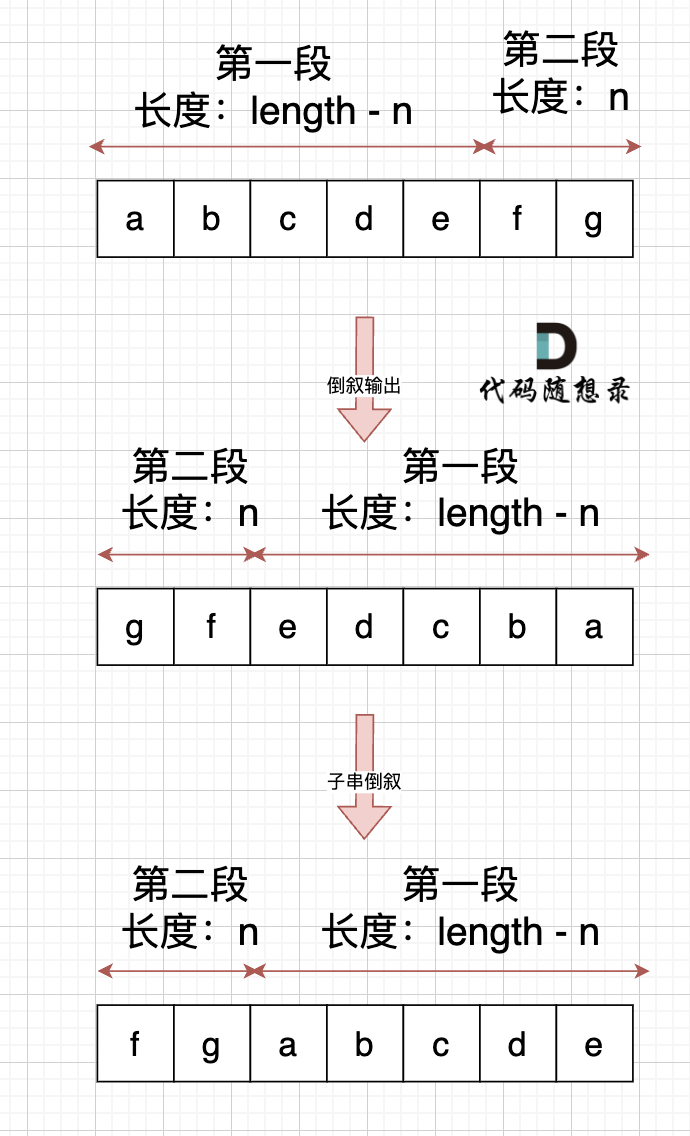
Essentially, the approach is to reverse the full string to flip the order of the two segments, and then reverse the characters within each segment. This results in achieving the correct character order within each segment through a concept akin to a "double negative."

The complete code is as follows:

// Version 1
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); // Get the length

    reverse(s.begin(), s.end()); // Global reversal
    reverse(s.begin(), s.begin() + n); // Reverse the first segment, length n
    reverse(s.begin() + n, s.end()); // Reverse the second segment

    cout << s << endl;
} 

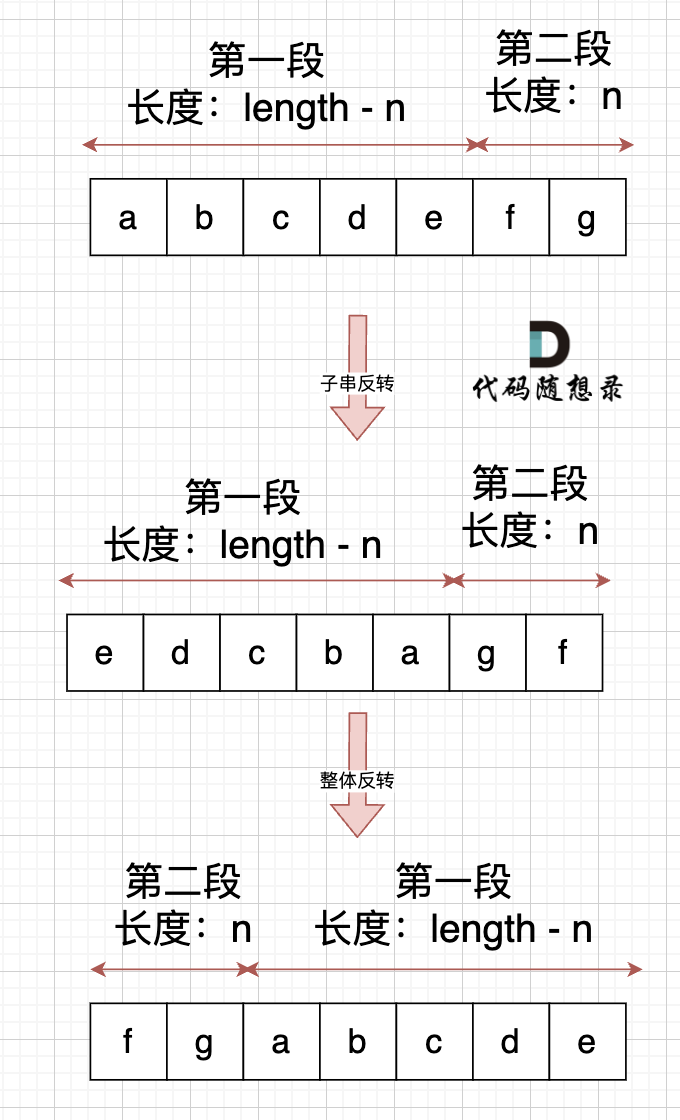
Can we perform local reversal first before global reversal? Yes, but remember to control the length of the local reversal. If you perform local reversal first, the length of the first reversed segment is len - n, as shown:

Here is the code:

// Version 2 
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); // Get the length
    reverse(s.begin(), s.begin() + len - n); // Reverse the first segment, length len-n 
    reverse(s.begin() + len - n, s.end()); // Reverse the second segment
    reverse(s.begin(), s.end()); // Global reversal
    cout << s << endl;
}

Extension

In some problems from the "Sword Offer," you will find problems about left rotation. What is the difference between left and right rotation?

The thought process is essentially the same; the difference lies in the segments being reversed. If this problem was about left rotating by n positions, the implementation would look like this:

#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); // Get the length
    reverse(s.begin(), s.begin() + n); // Reverse the first segment, length n
    reverse(s.begin() + n, s.end()); // Reverse the second segment, length len-n
    reverse(s.begin(), s.end()); // Global reversal
    cout << s << endl;
}

Observe the differences between this code and Version 2—they lie entirely in the reversal intervals.

Can left rotation be achieved by performing a global reversal first, just like in Version 1? Certainly.

Other Language Versions

Java:

Python:

Go:

JavaScript:

TypeScript:

Swift:

PHP:

Scala:

Rust: