1971. Find if Path Exists in Graph

Problem Link (opens new window)

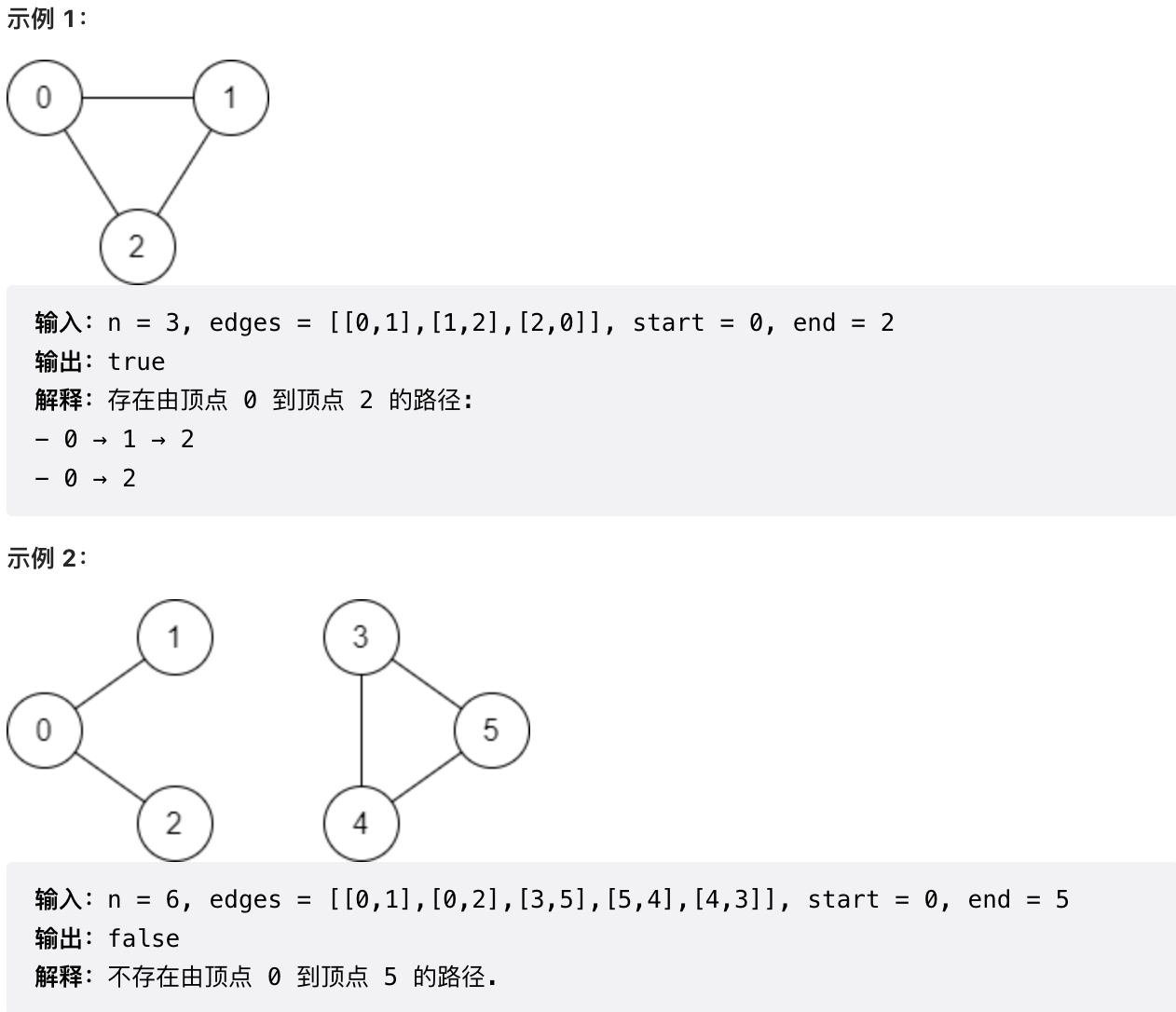
There is an undirected graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented by a 2D integer array edges, where edges[i] = [ui, vi] indicates that there is an undirected edge between vertex ui and vertex vi. Each vertex pair is connected by at most one edge, and no vertex has an edge to itself.

Your task is to determine if there is a valid path that exists from vertex start to vertex end.

Given the array edges and the integers n, start, and end, return true if there is a valid path from start to end, otherwise return false.

Approach

This problem is a basic application of Union-Find (Disjoint Set). If you're not familiar with Union-Find, you can check here: Union-Find Theoretical Basis (opens new window)

What problems can Union-Find solve?

Primarily, it helps in dealing with problems related to sets, such as determining if two nodes belong to the same set or grouping two nodes into one set.

Here's a template of my Union-Find implementation:

int n = 1005; // Set n according to the number of nodes in the problem, generally a bit larger than the number of nodes
vector<int> father = vector<int> (n, 0); // An array structure in C++

void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}

int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // Path compression
}

// Using an iterative method to avoid stack overflow problems
int find(int x) {
  while (x != parent[x]) {
	// Path compression, directly linking x to its ancestor node, reducing tree height
	parent[x] = parent[parent[x]];
	x = parent[x];
	}
return x;
}

bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

void join(int u, int v) {
    u = find(u); // Find the root of u
    v = find(v); // Find the root of v
    if (u == v) return; // If the roots are the same, they're in the same set, no need to connect
    father[v] = u;
}

In the above template, just modify the size of n. The problem guarantees n does not exceed 2 * 10^5.

The Union-Find mainly has three functions.

1. Find the root node using find(int u), which determines the ancestor node of a given node.
2. Connect two nodes into the same set using join(int u, int v), linking both nodes to the same root node.
3. Check if two nodes belong to the same set using isSame(int u, int v), essentially checking if they share the same root node.

Having briefly introduced Union-Find, let's examine this problem.

Why is this considered a fundamental Union-Find problem? The problem involves an undirected graph, hence determining if there exists a valid path between two vertices is equivalent to checking if these two vertices are in the same set.

How do we define being in the same set? If there's an edge connecting them, they're in the same set.

Thus, we can directly apply the Union-Find template.

Please use the iterative method in the join(int u, int v) function to avoid stack overflow when invoking find.

Use join(int u, int v) to add each edge to the Union-Find.

Finally, determine if they share the same root with isSame(int u, int v).

Here's the implementation in C++:

class Solution {
private:
    int n = 200005;
    vector<int> father = vector<int> (n, 0);

    void init() {
        for (int i = 0; i < n; ++i) { father[i] = i;
        }
    }

    int find(int x) {
      while (x != parent[x]) {
	      parent[x] = parent[parent[x]];
	      x = parent[x];
	      }
      return x;
    }

    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return;
        father[v] = u;
    }

public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        init();
        for (int i = 0; i < edges.size(); i++) {
            join(edges[i][0], edges[i][1]);
        }
        return isSame(source, destination);
    }
};

Versions in Other Languages

Java:

class Solution {

    int[] father;
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        father = new int[n];
        init();
        for (int i = 0; i < edges.length; i++) {
            join(edges[i][0], edges[i][1]);
        }

        return isSame(source, destination);
    }

    public void init() {
        for (int i = 0; i < father.length; i++) {
            father[i] = i;
        }
    }

    public int find(int u) {
        if (u == father[u]) {
            return u;
        } else {
            father[u] = find(father[u]);
            return father[u];
        }
    }

    public boolean isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    public void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return;
        father[v] = u;
    }
}

Python:

The PYTHON Union-Find implementation is shown below:

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        p = [i for i in range(n)]
        def find(i):
            if p[i] != i:
                p[i] = find(p[i])
            return p[i]
        for u, v in edges:
            p[find(u)] = find(v)
        return find(source) == find(destination)

JavaScript:

The JavaScript Union-Find solution is as follows:

class unionF{
    constructor(n){
        this.count = n
        this.roots = new Array(n).fill(0).map((item,index)=>index)
    }

    findRoot(x){
        if(this.roots[x]!==x){
            this.roots[x] = this.findRoot(this.roots[x])
        }
        return this.roots[x]
    }

    union(x,y){
        const rx = this.findRoot(x)
        const ry = this.findRoot(y)
        this.roots[rx] = ry
        this.count--
    }

    isConnected(x,y){
        return this.findRoot(x)===this.findRoot(y)
    }
}

var validPath = function(n, edges, source, destination) {
    const UF = new unionF(n)
    for(const [s,t] of edges){
        UF.union(s,t)
    }
    return UF.isConnected(source,destination)
};

The JavaScript bidirectional BFS solution is as follows:

var validPath = function(n, edges, source, destination) {
    const graph = new Array(n).fill(0).map(()=>[])
    for(const [s,t] of edges){
        graph[s].push(t)
        graph[t].push(s)
    }

    const visited = new Array(n).fill(false)
    function bfs(start,end,graph){
        const startq = [start]
        const endq = [end]
        while(startq.length&&endq.length){
            const slen = startq.length
            for(let i = 0;i<slen;i++){
                const scur = startq.shift()
                if(visited[scur]) continue
                if(endq.includes(scur)) return true
                visited[scur] = true
                const neighbors = graph[scur]
                startq.push(...neighbors)
            }

            const elen = endq.length
            for(let i = 0;i<elen;i++){
                const ecur = endq.shift()
                if(visited[ecur]) continue
                if(startq.includes(ecur)) return true
                visited[ecur] = true
                const neighbors = graph[ecur]
                endq.push(...neighbors)
            }
        }
        return false
    }
    return bfs(source,destination,graph)
};

Go

func validPath(n int, edges [][]int, source int, destination int) bool {
	n = 200005
	father := make([]int, n)
	for i := 0; i < n; i++ {
		father[i] = i
	}

	var find func(u int) int
	find = func(u int) int {
		if u == father[u] {
			return u
		}
		return find(father[u])
	}

	var join func(u, v int)
	join = func(u, v int) {
		u = find(u)
		v = find(v)
		if u == v {
			return
		}
		father[v] = u
	}

	for i := 0; i < len(edges); i++ {
		join(edges[i][0], edges[i][1])
	}

	source = find(source)
	destination = find(destination)
	return source == destination
}