# 1365. How Many Numbers Are Smaller Than the Current Number

LeetCode Problem Link (opens new window)

Given the array nums, for each element nums[i], count how many numbers in the array are smaller than it.

In other words, for each nums[i], you must compute the number of valid indices j such that j != i and nums[j] < nums[i].

Return the answer as an array.

Example 1:

Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: For nums[0]=8 there are four numbers smaller than it (1, 2, 2, and 3). For nums[1]=1 there are no numbers smaller than it. For nums[2]=2 there is one number smaller than it (1). For nums[3]=2 there is one number smaller than it (1). For nums[4]=3 there are three numbers smaller than it (1, 2, and 2).

Example 2:

Input: nums = [6,5,4,8]
Output: [2,1,0,3]

Example 3:

Input: nums = [7,7,7,7]
Output: [0,0,0,0]

Constraints:

2 <= nums.length <= 500
0 <= nums[i] <= 100

# Approach

A straightforward way is to use two nested for loops for a brute force search, which clearly has a time complexity of $O(n^2)$.

Let's consider how to optimize this.

First, to find how many numbers are smaller than the current number, we can sort the array in increasing order. After sorting, each number's index will represent the count of numbers smaller than it.

So, we can define a new array and sort it.

After sorting, the index of each number actually represents the count of numbers smaller than it.

The code is as follows:

vector<int> vec = nums;
sort(vec.begin(), vec.end()); // After sorting in ascending order, an element's index represents the count of numbers smaller than it.

1
2

Use a hash table hash (here, we can simply use an array) to map values to indices, allowing us to quickly determine the index for any value (i.e., how many numbers are smaller than it).

An edge case is when numbers are identical.

For example, in the array: 1 2 3 4 4 4, the index for the first number 4 is 3, and for the second number 4, the index is 4.

Here, a small trick is needed: when constructing the hash array, traverse from back to front, so that hash stores the leftmost index of identical elements. The code is as follows:

int hash[101];
for (int i = vec.size() - 1; i >= 0; i--) { // Record the index of vec[i] from back to front
    hash[vec[i]] = i;
}

1
2
3
4

Finally, traverse the original array nums, and use hash to quickly find the count of numbers smaller than each value. Store the result in another array.

The code is as follows:

// At this point, hash stores the count of numbers smaller than each element
for (int i = 0; i < nums.size(); i++) {
    vec[i] = hash[nums[i]];
}

1
2
3
4

The process is illustrated in the following image:

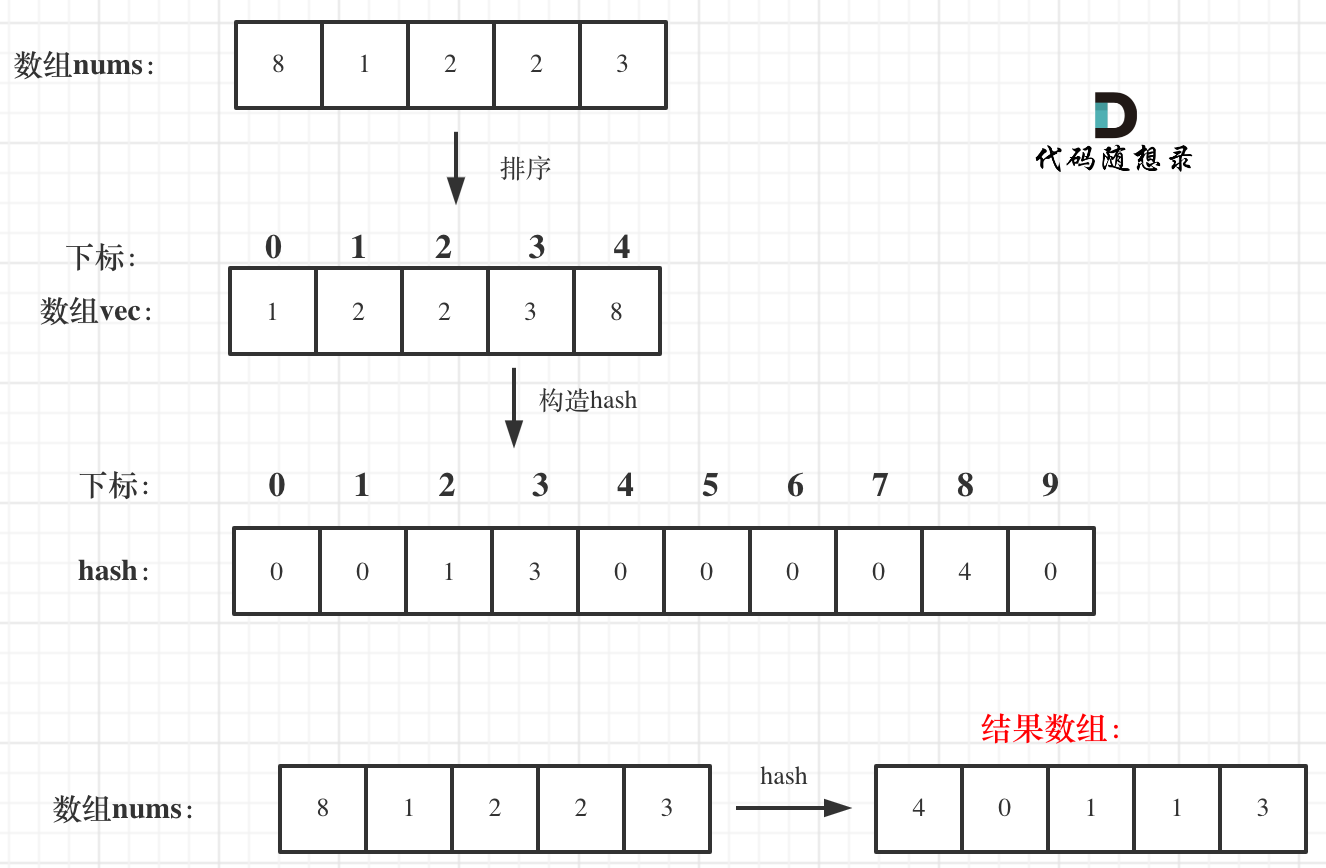
The key parts are explained; the complete C++ code is as follows:

class Solution {
public:
    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
        vector<int> vec = nums;
        sort(vec.begin(), vec.end()); // After sorting in ascending order, an element's index represents the count of numbers smaller than it.
        int hash[101];
        for (int i = vec.size() - 1; i >= 0; i--) { // Record the index of vec[i] from back to front
            hash[vec[i]] = i;
        }
        // At this point, hash stores the count of numbers smaller than each element
        for (int i = 0; i < nums.size(); i++) {
            vec[i] = hash[nums[i]];
        }
        return vec;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Using sorting and a hash table gives us a time complexity of $O(n\log n)$.

# Other Language Versions

# Java:

public int[] smallerNumbersThanCurrent(int[] nums) {
    Map<Integer, Integer> map = new HashMap<>(); // Record the number of nums[i] that are smaller than it
    int[] res = Arrays.copyOf(nums, nums.length);
    Arrays.sort(res);
    for (int i = 0; i < res.length; i++) {
        if (!map.containsKey(res[i])) { // When encountering the same number, do not update the number's situation
            map.put(res[i], i);
        }
    }

    for (int i = 0; i < nums.length; i++) {
        res[i] = map.get(nums[i]);
    }

    return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Python:

Brute Force Method:

class Solution:
    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
        res = [0 for _ in range(len(nums))]
        for i in range(len(nums)):
            cnt = 0
            for j in range(len(nums)):
                if j == i:
                    continue
                if nums[i] > nums[j]:
                    cnt += 1
            res[i] = cnt
        return res

1
2
3
4
5
6
7
8
9
10
11
12

Sorting + Hash:

class Solution:
    # Method 1: Using Dictionary
    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
        res = nums[:]
        hash_dict = dict()
        res.sort() # After sorting in ascending order, an element's index represents the count of numbers smaller than it.
        for i, num in enumerate(res):
            if num  not in hash_dict.keys(): # When encountering the same number, do not update the number's situation
                hash_dict[num] = i       
        for i, num in enumerate(nums):
            res[i] = hash_dict[num]
        return res

    # Method 2: Using Array
    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
        # Simultaneously sort and create a new array to reduce one redundant array copy operation, reducing one O(n) copy time cost
        sort_nums = sorted(nums)
        # According to the description 0 <= nums[i] <= 100, so the parameter setting for range is 101
        hash_lst = [0 for _ in range(101)]
        # Traverse from back to front, so that hash stores the leftmost value and index of identical elements
        for i in range(len(sort_nums)-1,-1,-1):
            hash_lst[sort_nums[i]] = i
        for i in range(len(nums)):
            nums[i] = hash_lst[nums[i]]
        return nums

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# Go:

func smallerNumbersThanCurrent(nums []int) []int {
    // Map, key[value in array], value[number of values smaller than key]
    m := make(map[int]int)
    // Copy the original array
    rawNums := make([]int,len(nums)) 
    copy(rawNums,nums)
    // Sort the array
    sort.Ints(nums)
    // Loop through the sorted array, value is the map key, index is the value
    for i,v := range nums {
        _,contains := m[v]
        if !contains {
          m[v] = i
        }   
    }
    // Result array
    result := make([]int,len(nums))
    // According to the position in the original array, store the corresponding number of smaller numbers
    for i,v := range rawNums {
        result[i] = m[v]
    }

    return result
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# JavaScript:

// Method 1: Use a hash table to record positions
var smallerNumbersThanCurrent = function(nums) {
    const map = new Map(); // Record the number of nums[i] that are smaller than it
    const res = nums.slice(0); // Deep copy of nums
    res.sort((a,b) => a - b);
    for(let i = 0; i < res.length; i++){
        if(!map.has(res[i])){ // When encountering the same number, do not update the number's situation
            map.set(res[i],i);
        }
    }
    // At this point, map stores the count of numbers smaller than each element
    for(let i = 0; i < nums.length; i++){
        res[i] = map.get(nums[i]);
    }
    return res;
};

// Method 2: Use only one additional array, without a hash table
/**
 * @param {number[]} nums
 * @return {number[]}
 */
var smallerNumbersThanCurrent = function(nums) {
    let array = [...nums];   // Deep copy
    // Sort in ascending order; the index of an element is the count of numbers smaller than it
    array = array.sort((a, b) => a-b);
    let res = [];
    nums.forEach( x => {
        // Even if elements repeat, it doesn't matter; indexOf only returns the index of the first found element
        res.push(array.indexOf(x));
    })
    return res;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# TypeScript:

Brute Force Method:

function smallerNumbersThanCurrent(nums: number[]): number[] {
    const length: number = nums.length;
    const resArr: number[] = [];
    for (let i = 0; i < length; i++) {
        let count: number = 0;
        for (let j = 0; j < length; j++) {
            if (nums[j] < nums[i]) {
                count++;
            }
        }
        resArr[i] = count;
    }
    return resArr;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Sorting + Hash:

function smallerNumbersThanCurrent(nums: number[]): number[] {
    const length: number = nums.length;
    const sortedArr: number[] = [...nums];
    sortedArr.sort((a, b) => a - b);
    const hashMap: Map<number, number> = new Map();
    for (let i = length - 1; i >= 0; i--) {
        hashMap.set(sortedArr[i], i);
    }
    const resArr: number[] = [];
    for (let i = 0; i < length; i++) {
        resArr[i] = hashMap.get(nums[i]);
    }
    return resArr;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# Rust:

use std::collections::HashMap;
impl Solution {
    pub fn smaller_numbers_than_current(nums: Vec<i32>) -> Vec<i32> {
        let mut v = nums.clone();
        v.sort();
        let mut hash = HashMap::new();
        for i in 0..v.len() {
            // Use or_insert in Rust to insert the value, if present, do not insert, using forward traversal
            hash.entry(v[i]).or_insert(i as i32);
        }
        nums.into_iter().map(|x| *hash.get(&x).unwrap()).collect()
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13