1254. Number of Closed Islands

LeetCode Problem Link (opens new window)

A 2D grid grid is composed of 0 (land) and 1 (water). An island is a maximal group of 0s that is connected in the four cardinal directions. A closed island is an island that is completely surrounded by 1s (water).

Please return the number of closed islands.

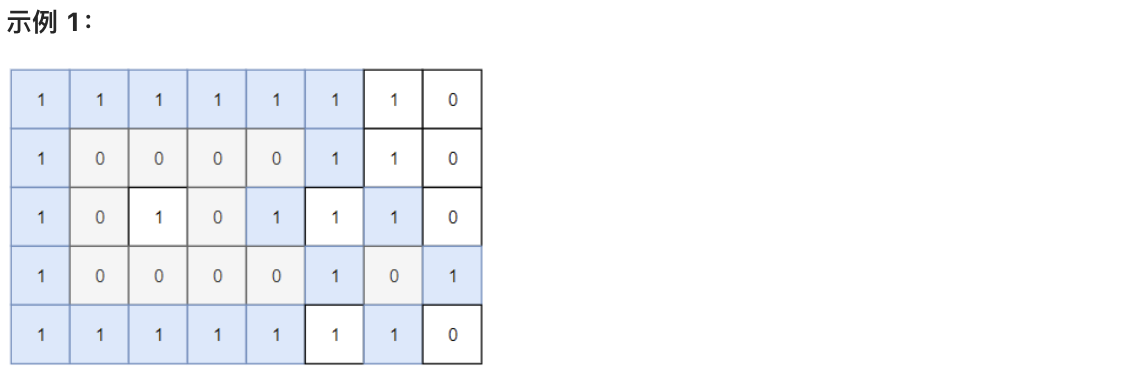
• Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
• Output: 2
• Explanation: The gray areas represent closed islands because they are completely surrounded by water (1s).

• Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
• Output: 1

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <= 1

Approach

The approach is similar to 1020. Number of Enclaves (opens new window). The code is also very similar.

class Solution {
private:
    int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // storing four directions
    void dfs(vector<vector<int>>& grid, int x, int y) {
        grid[x][y] = 1;
        for (int i = 0; i < 4; i++) { // traverse in four directions
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            // Boundary limits
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
            // Does not meet conditions, do not traverse further
            if (grid[nextx][nexty] == 1) continue;

            dfs(grid, nextx, nexty);
        }
        return;
    }

public:
    int closedIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        // Traverse from the left and right borders towards the middle
        for (int i = 0; i < n; i++) {
            if (grid[i][0] == 0) dfs(grid, i, 0);
            if (grid[i][m - 1] == 0) dfs(grid, i, m - 1);
        }
        // Traverse from the top and bottom borders towards the middle
        for (int j = 0; j < m; j++) {
            if (grid[0][j] == 0) dfs(grid, 0, j);
            if (grid[n - 1][j] == 0) dfs(grid, n - 1, j);
        }
        int count = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 0) {
                    count++;
                    dfs(grid, i, j);
                }
            }
        }
        return count;
    }
};

Other Language Versions

JavaScript:

/**
 * @param {number[][]} grid
 * @return {number}
 */
var closedIsland = function(grid) {
    let rows = grid.length;
    let cols = grid[0].length;
    // Store four directions
    let dir = [[-1, 0], [0, -1], [1, 0], [0, 1]];
    // Depth-first search
    function dfs(x, y) {
        grid[x][y] = 1;
        // Traverse in four directions
        for(let i = 0; i < 4; i++) {
            let nextX = x + dir[i][0];
            let nextY = y + dir[i][1];
            // Check boundaries
            if (nextX < 0 || nextX >= rows || nextY < 0 || nextY >= cols) continue;
            // Does not meet conditions
            if (grid[nextX][nextY] === 1) continue;
            // Continue recursion
            dfs(nextX, nextY);
        }
    }
    // Start from border islands
    // Traverse from left and right sides
    for(let i = 0; i < rows; i++) {
        if (grid[i][0] === 0) dfs(i, 0);
        if (grid[i][cols - 1] === 0) dfs(i, cols - 1);
    }
    // Traverse from top and bottom sides
    for(let j = 0; j < cols; j++) {
        if (grid[0][j] === 0) dfs(0, j);
        if (grid[rows - 1][j] === 0) dfs(rows - 1, j);
    }
    let count = 0;
    // After excluding all land connected to the border, 
    // Iterate through each grid element; if an element is land and unvisited, a new island is encountered. 
    // Increase the count of closed islands by 1, and explore all connected lands
    for(let i = 0; i < rows; i++) {
        for(let j = 0; j < cols; j++) {
            if (grid[i][j] === 0) {
                count++;
                dfs(i, j);
            }
        }
    }
    return count;
};