# 1020. Number of Enclaves
LeetCode Link (opens new window)
You are given an m x n binary matrix grid, where 0 represents an ocean cell and 1 represents a land cell.
A move is defined as walking from one land cell to an adjacent (up, down, left, or right) land cell or crossing the boundary of the grid.
Return the number of land cells in the grid that cannot reach the grid boundary in any number of moves.

- Input:
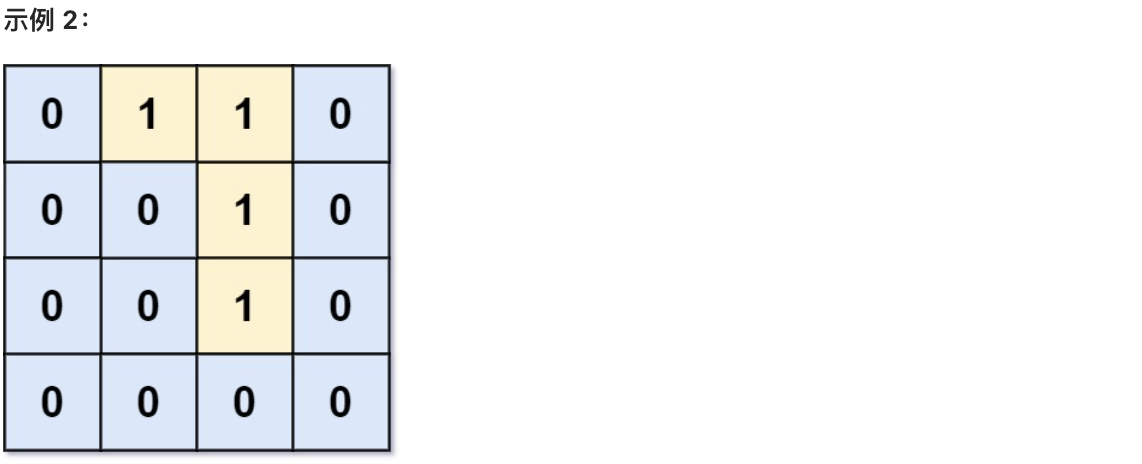
grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] - Output:
3 - Explanation: There are three
1s that are surrounded by0s. One1is not surrounded because it is on the boundary.
- Input:
grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] - Output:
0 - Explanation: All
1s are on the boundary or can reach the boundary.
# Approach
This problem can be solved using DFS, BFS, or a Union-Find (Disjoint Set Union, DSU) approach.
The task is to find the land area that is not adjacent to the boundary. We can start from the land on the boundary and change adjacent land cells connected by DFS or BFS to ocean. Then, when we traverse the map again, we can count the number of lands left.
As shown in the illustration, by traversing the four sides of the map, the land adjacent to the perimeter of the map turns green.
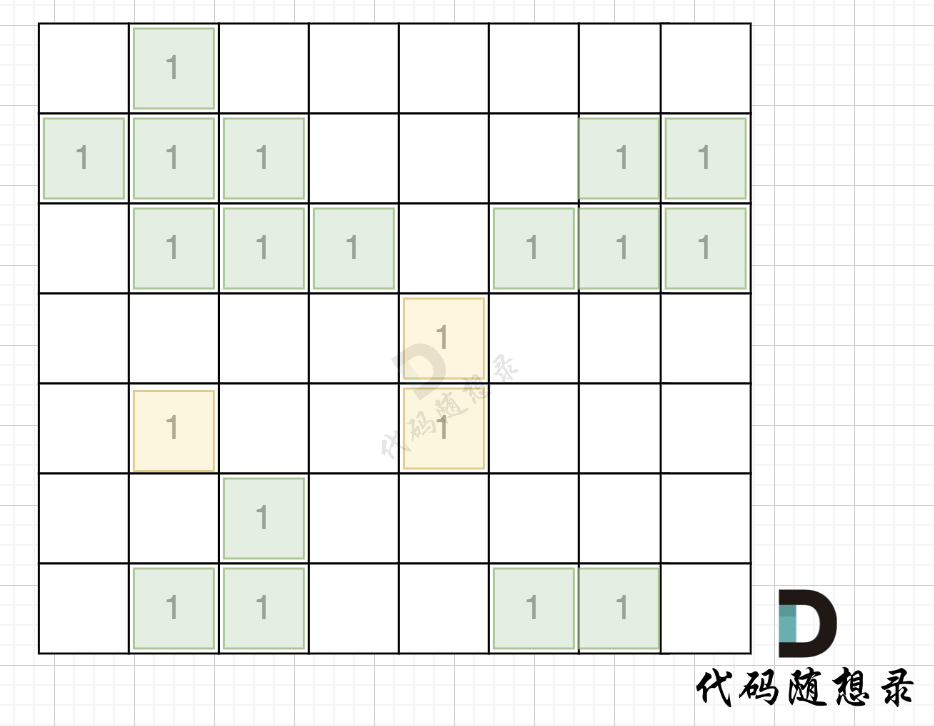
When land on the map perimeter is found, turn 1s into 0s, resulting in a map like this:
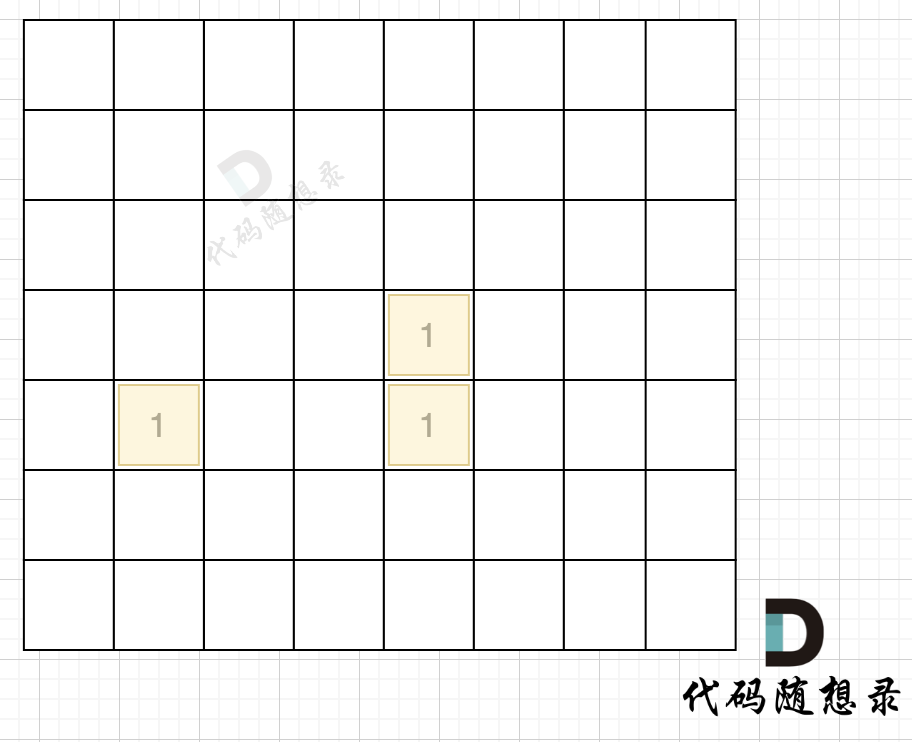
Then, traverse the map again, applying depth-first or breadth-first search on land cells to count them.
If you are unfamiliar with depth-first search or breadth-first search, it is recommended to check here: In-depth Explanation of Depth-First Search (opens new window), In-depth Explanation of Breadth-First Search (opens new window).
Below is the code using depth-first search:
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // Four directions
int count; // Count of land cells that meet the requirement
void dfs(vector<vector<int>>& grid, int x, int y) {
grid[x][y] = 0;
count++;
for (int i = 0; i < 4; i++) { // Traverse in four directions
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// Out of boundary
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
// Condition does not meet, stop traversing
if (grid[nextx][nexty] == 0) continue;
dfs(grid, nextx, nexty);
}
return;
}
public:
int numEnclaves(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
// Traverse from the left and right bounds toward the center
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) dfs(grid, i, 0);
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
}
// Traverse from the top and bottom bounds toward the center
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) dfs(grid, 0, j);
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) dfs(grid, i, j);
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
Here is the code using breadth-first search:
class Solution {
private:
int count = 0;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
void bfs(vector<vector<int>>& grid, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
grid[x][y] = 0; // Immediately mark when added to queue
count++;
while (!que.empty()) {
pair<int, int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // Out of boundary, skip
if (grid[nextx][nexty] == 1) {
que.push({nextx, nexty});
count++;
grid[nextx][nexty] = 0; // Immediately mark when added to queue
}
}
}
}
public:
int numEnclaves(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
// From the left and right edges, traverse toward the center
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) bfs(grid, i, 0);
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
}
// From the top and bottom edges, traverse toward the center
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) bfs(grid, 0, j);
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) bfs(grid, i, j);
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# Other Language Versions
# Java
Depth-First Search (DFS) without a termination condition and space optimization (flood the island, no visited array used)
// DFS
class Solution {
int count = 0;
int[][] dir ={
{0, 1},
{1, 0},
{-1, 0},
{0, -1}
};
private void dfs(int[][] grid, int x, int y){
if(grid[x][y] == 0)
return;
grid[x][y] = 0;
count++;
for(int i = 0; i < 4; i++){
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
continue;
dfs(grid, nextX, nextY);
}
}
public int numEnclaves(int[][] grid) {
for(int i = 0; i < grid.length; i++){
if(grid[i][0] == 1)
dfs(grid, i, 0);
if(grid[i][grid[0].length - 1] == 1)
dfs(grid, i, grid[0].length - 1);
}
// Adjusted j's bounds to avoid unnecessary repeated operations.
for(int j = 1; j < grid[0].length - 1; j++){
if(grid[0][j] == 1)
dfs(grid, 0, j);
if(grid[grid.length - 1][j] == 1)
dfs(grid, grid.length - 1, j);
}
count = 0;
for(int i = 1; i < grid.length - 1; i++){
for(int j = 1; j < grid[0].length - 1; j++){
if(grid[i][j] == 1)
dfs(grid, i, j);
}
}
return count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
Depth-First Search (DFS) without termination condition
class Solution {
// Four directions
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
// Depth-First Search, marking all 1s that can reach the boundary as true
public void dfs(int[][] grid, int row, int col, boolean[][] visited) {
for (int[] current: position) {
int newRow = row + current[0], newCol = col + current[1];
// Index out of bounds, skip
if (newRow < 0 || newRow >= grid.length || newCol < 0 || newCol >= grid[0].length) continue;
// Current position is not 1 or already visited
if (grid[newRow][newCol] != 1 || visited[newRow][newCol]) continue;
visited[newRow][newCol] = true;
dfs(grid, newRow, newCol, visited);
}
}
public int numEnclaves(int[][] grid) {
int rowSize = grid.length, colSize = grid[0].length, ans = 0; // `ans` records the result
// A boolean array marks each `1`'s position whether it can reach the boundary
boolean[][] visited = new boolean[rowSize][colSize];
// Traverse from the left and right edges toward the center
for (int row = 0; row < rowSize; row++) {
if (grid[row][0] == 1 && !visited[row][0]) {
visited[row][0] = true;
dfs(grid, row, 0, visited);
}
if (grid[row][colSize - 1] == 1 && !visited[row][colSize - 1]) {
visited[row][colSize - 1] = true;
dfs(grid, row, colSize - 1, visited);
}
}
// Traverse the top and bottom edges toward the center but skip the corners as they have been handled
for (int col = 1; col < colSize - 1; col++) {
if (grid[0][col] == 1 && !visited[0][col]) {
visited[0][col] = true;
dfs(grid, 0, col, visited);
}
if (grid[rowSize - 1][col] == 1 && !visited[rowSize - 1][col]) {
visited[rowSize - 1][col] = true;
dfs(grid, rowSize - 1, col, visited);
}
}
// Find unmarked `1`s and record into `ans`
for (int row = 0; row < rowSize; row++) {
for (int col = 0; col < colSize; col++) {
if (grid[row][col] == 1 && !visited[row][col]) ++ans;
}
}
return ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
Breadth-First Search (BFS) with a visited array
class Solution {
// Four directions
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
// Breadth-First Search, marking all `1`s that can reach the boundary as true
public void bfs(int[][] grid, Queue<int[]> queue, boolean[][] visited) {
while (!queue.isEmpty()) {
int[] curPos = queue.poll();
for (int[] current: position) {
int row = curPos[0] + current[0], col = curPos[1] + current[1];
// Index out of bounds, skip
if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length) continue;
// Current position is not 1 or already visited
if (visited[row][col] || grid[row][col] == 0) continue;
visited[row][col] = true;
queue.add(new int[]{row, col});
}
}
}
public int numEnclaves(int[][] grid) {
int rowSize = grid.length, colSize = grid[0].length, ans = 0; // `ans` records the result
// A boolean array marks each `1`'s position whether it can reach the boundary
boolean[][] visited = new boolean[rowSize][colSize];
Queue<int[]> queue = new ArrayDeque<>();
// Traverse from the left and right edges toward the center
for (int row = 0; row < rowSize; row++) {
if (grid[row][0] == 1) {
visited[row][0] = true;
queue.add(new int[]{row, 0});
}
if (grid[row][colSize - 1] == 1) {
visited[row][colSize - 1] = true;
queue.add(new int[]{row, colSize - 1});
}
}
// Traverse the top and bottom edges but skip the corners as they have been handled
for (int col = 1; col < colSize - 1; col++) {
if (grid[0][col] == 1) {
visited[0][col] = true;
queue.add(new int[]{0, col});
}
if (grid[rowSize - 1][col] == 1) {
visited[rowSize - 1][col] = true;
queue.add(new int[]{rowSize - 1, col});
}
}
bfs(grid, queue, visited); // Breadth-First Search
// Find unmarked `1`s and record into `ans`
for (int row = 0; row < rowSize; row++) {
for (int col = 0; col < colSize; col++) {
if (grid[row][col] == 1 && !visited[row][col]) ++ans;
}
}
return ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
Breadth-First Search (BFS) with space optimization (flood the island, no visited array used)
// BFS
class Solution {
int count = 0;
int[][] dir ={
{0, 1},
{1, 0},
{-1, 0},
{0, -1}
};
private void bfs(int[][] grid, int x, int y){
Queue<Integer> que = new LinkedList<>();
que.offer(x);
que.offer(y);
count++;
grid[x][y] = 0;
while(!que.isEmpty()){
int currX = que.poll();
int currY = que.poll();
for(int i = 0; i < 4; i++){
int nextX = currX + dir[i][0];
int nextY = currY + dir[i][1];
if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
continue;
if(grid[nextX][nextY] == 1){
que.offer(nextX);
que.offer(nextY);
count++;
grid[nextX][nextY] = 0;
}
}
}
}
public int numEnclaves(int[][] grid) {
for(int i = 0; i < grid.length; i++){
if(grid[i][0] == 1)
bfs(grid, i, 0);
if(grid[i][grid[0].length - 1] == 1)
bfs(grid, i, grid[0].length - 1);
}
for(int j = 1; j < grid[0].length; j++){
if(grid[0][j] == 1)
bfs(grid, 0 , j);
if(grid[grid.length - 1][j] == 1)
bfs(grid, grid.length - 1, j);
}
count = 0;
for(int i = 1; i < grid.length - 1; i++){
for(int j = 1; j < grid[0].length - 1; j++){
if(grid[i][j] == 1)
bfs(grid,i ,j);
}
}
return count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# Python
Depth-First Search (DFS)
class Solution:
def __init__(self):
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]] # Four directions
# Depth-First Search to mark all 1s that can reach the border as true
def dfs(self, grid: List[List[int]], row: int, col: int, visited: List[List[bool]]) -> None:
for current in self.position:
newRow, newCol = row + current[0], col + current[1]
# Initial index check
if newRow < 0 or newRow >= len(grid) or newCol < 0 or newCol >= len(grid[0]):
continue
# Current position isn't 1 or is already visited
if grid[newRow][newCol] == 0 or visited[newRow][newCol]: continue
visited[newRow][newCol] = True
self.dfs(grid, newRow, newCol, visited)
def numEnclaves(self, grid: List[List[int]]) -> int:
rowSize, colSize, ans = len(grid), len(grid[0]), 0
# Boolean array to track if a 1 position can reach the boundary or not
visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
# Check the left and right boundaries for 1s
for row in range(rowSize):
if grid[row][0] == 1:
visited[row][0] = True
self.dfs(grid, row, 0, visited)
if grid[row][colSize - 1] == 1:
visited[row][colSize - 1] = True
self.dfs(grid, row, colSize - 1, visited)
# Check the top and bottom boundaries for 1s but avoid the corners
for col in range(1, colSize - 1):
if grid[0][col] == 1:
visited[0][col] = True
self.dfs(grid, 0, col, visited)
if grid[rowSize - 1][col] == 1:
visited[rowSize - 1][col] = True
self.dfs(grid, rowSize - 1, col, visited)
# Find unmarked 1s and record them to the answer
for row in range(rowSize):
for col in range(colSize):
if grid[row][col] == 1 and not visited[row][col]:
ans += 1
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
Breadth-First Search (BFS)
class Solution:
def __init__(self):
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]] # Four directions
# Breadth-First Search, marking all 1s that can reach the boundary as true
def bfs(self, grid: List[List[int]], queue: deque, visited: List[List[bool]]) -> None:
while queue:
curPos = queue.popleft()
for current in self.position:
row, col = curPos[0] + current[0], curPos[1] + current[1]
# Index out of bounds
if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]): continue
# Current position isn't 1 or is visited
if grid[row][col] == 0 or visited[row][col]: continue
visited[row][col] = True
queue.append([row, col])
def numEnclaves(self, grid: List[List[int]]) -> int:
rowSize, colSize, ans = len(grid), len(grid[0]), 0
# Boolean array to track if a 1 position can reach the boundary or not
visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
queue = deque() # Queue
# Check the left and right boundaries for 1s
for row in range(rowSize):
if grid[row][0] == 1:
visited[row][0] = True
queue.append([row, 0])
if grid[row][colSize - 1] == 1:
visited[row][colSize - 1] = True
queue.append([row, colSize - 1])
# Check the top and bottom boundaries for 1s but avoid the corners
for col in range(1, colSize - 1):
if grid[0][col] == 1:
visited[0][col] = True
queue.append([0, col])
if grid[rowSize - 1][col] == 1:
visited[rowSize - 1][col] = True
queue.append([rowSize - 1, col])
self.bfs(grid, queue, visited) # Breadth-First Search
# Find unmarked 1s and record them to the result
for row in range(rowSize):
for col in range(colSize):
if grid[row][col] == 1 and not visited[row][col]:
ans += 1
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Go
DFS:
var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
var count int = 0
func numEnclaves(grid [][]int) int {
rows, cols := len(grid), len(grid[0])
// Rows
for i := range grid[0] {
if grid[0][i] == 1 {
dfs(grid, 0, i)
}
if grid[rows-1][i] == 1 {
dfs(grid, rows-1, i)
}
}
// Columns
for j := range grid {
if grid[j][0] == 1 {
dfs(grid, j, 0)
}
if grid[j][cols-1] == 1 {
dfs(grid, j, cols-1)
}
}
count = 0
for i := range grid {
for j := range grid[0] {
if grid[i][j] == 1 {
dfs(grid, i, j)
}
}
}
return count
}
func dfs(grid [][]int, i, j int) {
grid[i][j] = 0
count++
for _, d := range DIRECTIONS {
x, y := i+d[0], j+d[1]
if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
continue
}
if grid[x][y] == 1 {
dfs(grid, x, y)
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
BFS:
var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
var count int = 0
func numEnclaves(grid [][]int) int {
rows, cols := len(grid), len(grid[0])
// Rows
for i := range grid[0] {
if grid[0][i] == 1 {
bfs(grid, 0, i)
}
if grid[rows-1][i] == 1 {
bfs(grid, rows-1, i)
}
}
// Columns
for j := range grid {
if grid[j][0] == 1 {
bfs(grid, j, 0)
}
if grid[j][cols-1] == 1 {
bfs(grid, j, cols-1)
}
}
count = 0
for i := range grid {
for j := range grid[0] {
if grid[i][j] == 1 {
bfs(grid, i, j)
}
}
}
return count
}
func bfs(grid [][]int, i, j int) {
queue := [][]int{}
queue = append(queue, []int{i, j})
grid[i][j] = 0
count++
for len(queue) > 0 {
cur := queue[0]
queue = queue[1:]
for _, d := range DIRECTIONS {
x, y := cur[0]+d[0], cur[1]+d[1]
if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
continue
}
if grid[x][y] == 1 {
count++
queue = append(queue, []int{x, y})
grid[x][y] = 0
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# JavaScript
/**
* @param {number[][]} grid
* @return {number}
*/
var numEnclaves = function (grid) {
let row = grid.length;
let col = grid[0].length;
let count = 0;
// Check the first and last row, if there is a 1, then change all the connected 1s to 0 and don't count them.
for (let j = 0; j < col; j++) {
if (grid[0][j] === 1) {
dfs(0, j, false);
}
if (grid[row - 1][j] === 1) {
dfs(row - 1, j, false);
}
}
// Check the first and last column, if there is a 1, then change all the connected 1s to 0 and don't count them.
for (let i = 0; i < row; i++) {
if (grid[i][0] === 1) {
dfs(i, 0, false);
}
if (grid[i][col - 1] === 1) {
dfs(i, col - 1, false);
}
}
// Check the rest of the grid, if there is a 1, then change all the connected 1s to 0 and count them.
for (let i = 1; i < row - 1; i++) {
for (let j = 1; j < col - 1; j++) {
dfs(i, j, true);
}
}
function dfs(i, j, isCounting) {
let condition = i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === 0;
if (condition) return;
if (isCounting) count++;
grid[i][j] = 0;
dfs(i - 1, j, isCounting);
dfs(i + 1, j, isCounting);
dfs(i, j - 1, isCounting);
dfs(i, j + 1, isCounting);
}
return count;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# Rust
DFS:
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
for i in 0..grid.len() {
for j in 0..grid[0].len() {
if (i == 0 || i == grid.len() - 1 || j == 0 || j == grid[0].len() - 1)
&& grid[i][j] == 1
{
Self::dfs(&mut grid, (i as i32, j as i32));
}
}
}
grid.iter()
.map(|nums| nums.iter().filter(|&&num| num == 1).count() as i32)
.sum()
}
pub fn dfs(grid: &mut [Vec<i32>], (x, y): (i32, i32)) {
grid[x as usize][y as usize] = 0;
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (x + dx, y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
if grid[nx as usize][ny as usize] == 0 {
continue;
}
Self::dfs(grid, (nx, ny));
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
BFS:
use std::collections::VecDeque;
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
for i in 0..grid.len() {
for j in 0..grid[0].len() {
if (i == 0 || i == grid.len() - 1 || j == 0 || j == grid[0].len() - 1)
&& grid[i][j] == 1
{
// Self::dfs(&mut grid, (i as i32, j as i32));
Self::bfs(&mut grid, (i as i32, j as i32));
}
}
}
grid.iter()
.map(|nums| nums.iter().filter(|&&num| num == 1).count() as i32)
.sum()
}
pub fn bfs(grid: &mut [Vec<i32>], (x, y): (i32, i32)) {
let mut queue = VecDeque::new();
queue.push_back((x, y));
grid[x as usize][y as usize] = 0;
while let Some((cur_x, cur_y)) = queue.pop_front() {
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (cur_x + dx, cur_y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
if grid[nx as usize][ny as usize] == 0 {
continue;
}
queue.push_back((nx, ny));
grid[nx as usize][ny as usize] = 0;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Similar Problems
- 1254.Number of Closed Islands
