841. Keys and Rooms

LeetCode Problem Link (opens new window)

There are N rooms, and you start in room 0. Each room has a distinct number: 0, 1, 2, ..., N-1, and each room may contain some keys to access the next room.

Formally, each room i has a key list rooms[i], and each key rooms[i][j] is an integer in [0,1,...,N-1] where N = rooms.length. A key rooms[i][j] = v can open the room numbered v.

Initially, all rooms except room 0 are locked.

You can move freely between rooms.

If you can access every room, return true; otherwise, return false.

Example 1:

• Input: [[1],[2],[3],[]]
• Output: true
• Explanation: We start with room 0 and pick up key 1. Then we go to room 1 and pick up key 2. Then we go to room 2 and pick up key 3. Finally, we go to room 3. Since we were able to enter every room, we return true.

Example 2:

• Input: [[1,3],[3,0,1],[2],[0]]
• Output: false
• Explanation: We cannot enter room 2.

Thought Process

This problem essentially gives us a directed graph. Recognizing this as a directed graph is crucial!

For the two example graphs: [[1],[2],[3],[]] and [[1,3],[3,0,1],[2],[0]], visualizations of the corresponding graphs are as follows:

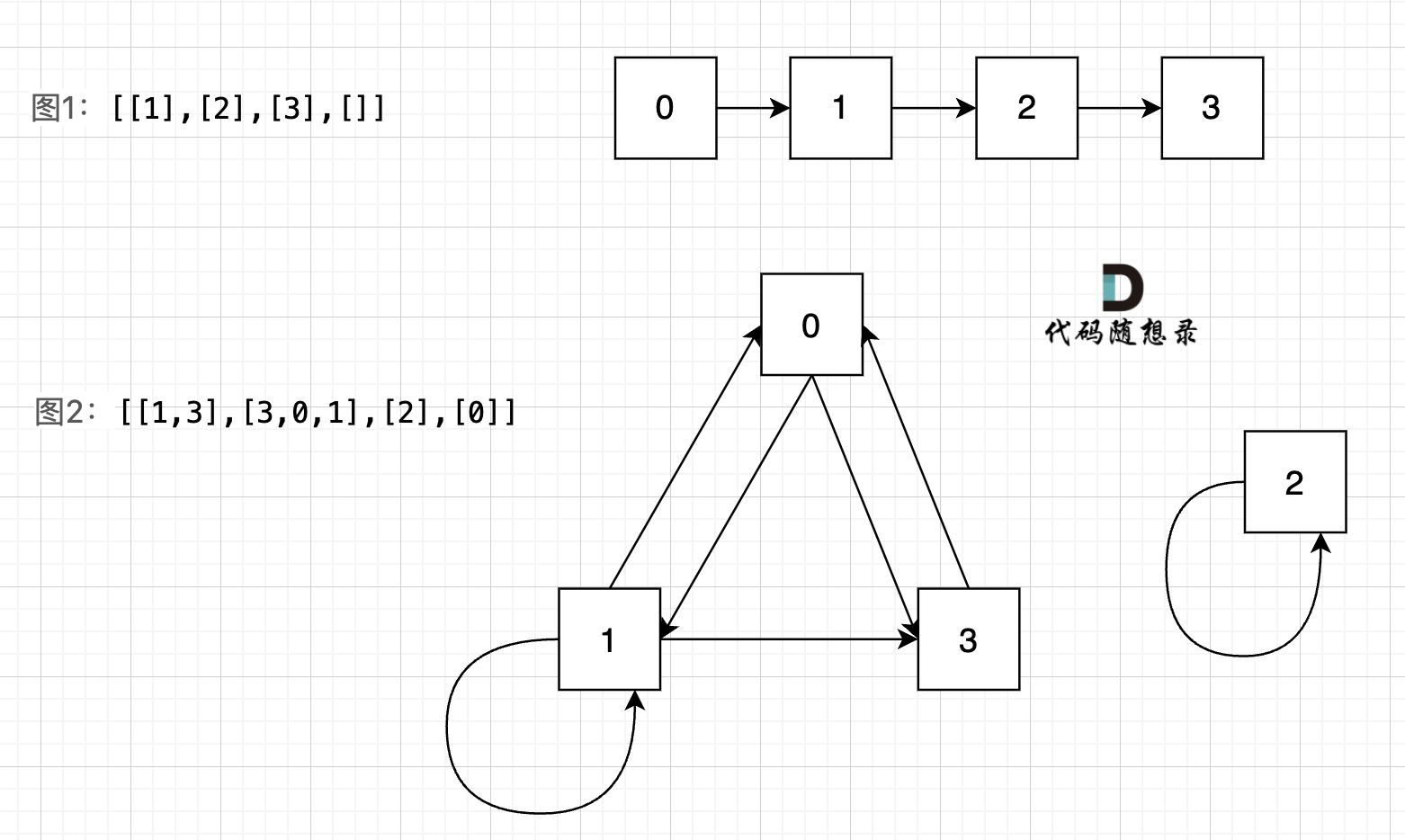
We can see that all nodes in Graph 1 are connected, while Node 2 in Graph 2 is isolated.

This easily reminds us of the island problem. As soon as we find an isolated island, it means we cannot enter all the rooms.

This naturally suggests using a union-find method.

But note that this is a directed graph! In a directed graph, even if all nodes are connected, it's still not possible to traverse all edges from node 0. Here's an example:

Graph 3: [[5], [], [1, 3], [5]] is visualized as:

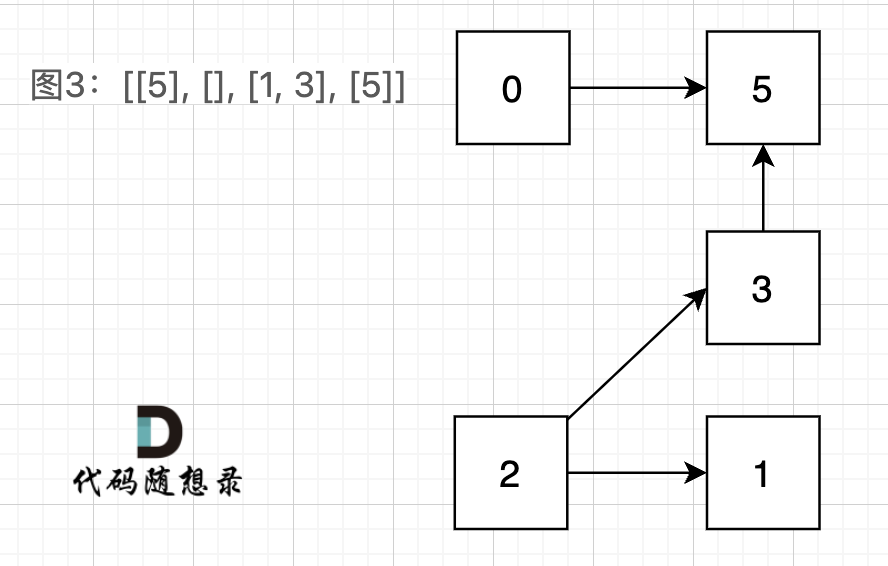
In Graph 3, you'll notice node 0 can only reach node 5 and then go nowhere.

Thus, this problem is about finding a path in a directed graph. We can solve it using either depth-first search (DFS) or breadth-first search (BFS).

For the DFS theory, if you have any confusion, you may refer to my article: Graph DFS Basics (opens new window).

There are two DFS methods in this problem. Please read carefully as many solutions do not make this clear. By understanding, you'll gain a deeper insight into DFS.

DFS in Three Steps:

1. Define the Recursive Function and Parameters

   We need to pass the 2D array rooms to traverse the map. We also need to know the current key we have to move to the next room.

   Additionally, we need an array to record which rooms we've been to so we can check if we've traversed all rooms. This can be a 1D array.

   Thus, the function parameters are as follows:

   // key represents the current key obtained
   // visited records the rooms visited
   void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
   

2. Define the Termination Condition

   When should the traversal stop?

   Here, it's essential to note the logical key: Are we processing the current visited node, or the next node to be visited in the recursion?

   This determines how the termination condition should be written.

   Firstly, in this problem, processing means marking the node as visited using the visited array, which initially contains all false. Changing a node's state to true means processing it.

   If we are processing the current visited node, and if it's true, that indicates the node has already been visited, so we terminate the current recursion. Otherwise, we mark it as true because we're processing the current recursion's node.

   The code would be like this:

   // Version 1: Process the current visited node
   void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
       if (visited[key]) { // If this recursion layer is true, it's visited, so immediately return
           return;
       }
       visited[key] = true; // Mark the current traversed node as true
       vector<int> keys = rooms[key];
       for (int key : keys) {
           // Depth-first search traversal
           dfs(rooms, key, visited);
       }
   }
   

   If we are processing the next layer to visit, instead of the current one, then there's no need for a termination condition, but while processing the current node paths to the next node, directly check if the next node should be traversed.

   The code would look like this:

   // Version 2: Process the next node to visit
   void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
       // Here there's no termination condition, but while processing the paths, determine if traversing is needed
       vector<int> keys = rooms[key];
       for (int key : keys) {
           if (visited[key] == false) { // For the next layer, determine if recursion is required
               visited[key] = true;
               dfs(rooms, key, visited);
           }
       }
   }
   

   As can be seen, how we view the node to visit directly forms two different implementations. For many, this aspect remains nebulous, and they may have completed the problem but not contemplated this depth of understanding.

3. Process the Current Node's Paths

   As discussed above, the variations in step two of the DFS execution directly form two separate recursion implementations.

   Here's another detail:

   In the above DFS methods, there seems to be no backtracking logic.

   We all know recursion features backtracking, occurring after the recursive function. However, why doesn't this problem have a backtracking operation, unlike previous DFS problems, such as 797. All Paths From Source to Target (opens new window)?

   In the code for both DFS implementations, there's no backtracking below the dfs function.

   You must consider the problem's requirements. This problem needs to determine if node 0 can reach all nodes, so there's no need to backtrack and revoke actions — just mark all traversed nodes indiscriminately.

   When is backtracking needed?

   When searching for a feasible path, backtracking is necessary because, without it, you can't "turn back." If this is hard to understand, please read my explanation on 797. All Paths From Source to Target (opens new window).

The above analysis is complete. Below is the full DFS implementation in C++:

// Version 1: Process the current visited node
class Solution {
private:
    void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
        if (visited[key]) {
            return;
        }
        visited[key] = true;
        vector<int> keys = rooms[key];
        for (int key : keys) {
            // Depth-first search traversal
            dfs(rooms, key, visited);
        }
    }
public:
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        vector<bool> visited(rooms.size(), false);
        dfs(rooms, 0, visited);
        // Check if all were visited
        for (int i : visited) {
            if (i == false) return false;
        }
        return true;
    }
};

// Version 2: Process the next node to visit
class Solution {
private:  
    void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
        vector<int> keys = rooms[key];
        for (int key : keys) {
            if (visited[key] == false) {
                visited[key] = true;
                dfs(rooms, key, visited);
            }
        }
    }
public:
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        vector<bool> visited(rooms.size(), false); 
        visited[0] = true; // Node 0 is the start and must be visited
        dfs(rooms, 0, visited);  
        // Check if all were visited
        for (int i : visited) {
            if (i == false) return false;
        }
        return true;
    }
};

For completeness, the BFS C++ code is also provided. For BFS theory, refer to Graph BFS Basics (opens new window). Here is the code:

class Solution {
    bool bfs(const vector<vector<int>>& rooms) {
        vector<int> visited(rooms.size(), 0); // Marks whether a room has been visited
        visited[0] = 1; // Start from room 0
        queue<int> que;
        que.push(0); // Start from room 0

        // Breadth-first search process
        while (!que.empty()) {
            int key = que.front(); que.pop();
            vector<int> keys = rooms[key];
            for (int key : keys) {
                if (!visited[key]) {
                    que.push(key);
                    visited[key] = 1;
                }
            }
        }
        // Check if all rooms have been traversed
        for (int i : visited) {
            if (i == 0) return false;
        }
        return true;
    }
public:
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        return bfs(rooms);
    }
};

Other Language Versions

Java

class Solution {
     private void dfs(int key, List<List<Integer>>  rooms, List<Boolean> visited) {
        if (visited.get(key)) {
            return;
        }
        visited.set(key, true);
        for (int k : rooms.get(key)) {
            // Depth-first search traversal
            dfs(k, rooms, visited);
        }
    }
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        List<Boolean> visited = new ArrayList<Boolean>(){{
            for(int i = 0 ; i < rooms.size(); i++){
                add(false);
            }
        }};
        dfs(0, rooms, visited);
        // Check if all were visited
        for (boolean flag : visited) {
            if (!flag) {
                return false;
            }
        }
        return true;
    }
}

// Breadth-first search
class Solution {
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        boolean[] visited = new boolean[rooms.size()];    // Tracks room visit status
        visited[0] = true;
        Queue<Integer> queue = new ArrayDeque<>();
        queue.add(0);           // Room 0 marked as visited
        while (!queue.isEmpty()) {
            int curKey = queue.poll();
            for (int key: rooms.get(curKey)) {
                if (visited[key]) continue;
                visited[key] = true;
                queue.add(key);
            }
        }
        for (boolean key: visited)
            if (!key) return false;
        return true;
    }
}

// Breadth-first traversal (time optimization)
class Solution {
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        int count = 1;      // Holds count of rooms that can be visited; starting from room 0, hence set to 1
        boolean[] visited = new boolean[rooms.size()];      // Tracks room visit status
        visited[0] = true;          // Room 0 marked as visited
        Queue<Integer> queue = new ArrayDeque<>();
        queue.add(0);
        while (!queue.isEmpty()) {
            int curKey = queue.poll();
            for (int key: rooms.get(curKey)) {
                if (visited[key]) continue;
                ++count;                // Increment count upon visiting a new room
                visited[key] = true;
                queue.add(key);
            }
        }
        return count == rooms.size();       // If count equals number of rooms, all rooms are visited; otherwise, they are not
    }
}

Python3

# Depth-first search
class Solution:
    def dfs(self, key: int, rooms: List[List[int]]  , visited : List[bool] ) :
        if visited[key] :
            return
        visited[key] = True
        keys = rooms[key]
        for i in range(len(keys)) :
            # Depth-first search traversal
            self.dfs(keys[i], rooms, visited)

    def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
        visited = [False for i in range(len(rooms))]

        self.dfs(0, rooms, visited)

        # Check if all were visited
        for i in range(len(visited)):
            if not visited[i] :
                return False
        return True

# Breadth-first search
class Solution:
    def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
        visited = [False] * len(rooms)
        self.bfs(rooms, 0, visited)
        
        for room in visited:
            if room == False:
                return False
        
        return True
    
    def bfs(self, rooms, index, visited):
        q = collections.deque()
        q.append(index)

        visited[0] = True

        while len(q) != 0:
            index = q.popleft()
            for nextIndex in rooms[index]:
                if visited[nextIndex] == False:
                    q.append(nextIndex)
                    visited[nextIndex] = True

Go

func dfs(key int, rooms [][]int, visited []bool ) {
	if visited[key] {
		return;
	}

	visited[key] = true
	keys := rooms[key]
	for _ , key := range keys {
		// Depth-first search traversal
		dfs(key, rooms, visited);
	}
}

func canVisitAllRooms(rooms [][]int) bool {
	visited := make([]bool, len(rooms));
	dfs(0, rooms, visited);
	// Check if all were visited
	for i := 0; i < len(visited); i++ {
		if !visited[i] {
			return false;
		}
	}
	return true;
}

JavaScript

// DFS
var canVisitAllRooms = function(rooms) {
    const dfs = (key, rooms, visited) => {
        if(visited[key]) return;
        visited[key] = 1;
        for(let k of rooms[key]){
            // Depth-first search traversal
            dfs(k, rooms, visited);
        }
    }
    const visited = new Array(rooms.length).fill(false);
    dfs(0, rooms, visited);
    // Check if all were visited
    for (let i of visited) {
        if (!i) {
            return false;
        }
    }
    return true;
};

// BFS
var canVisitAllRooms = function(rooms) {
    const bfs = rooms => {
        const visited = new Array(rooms.length).fill(0); // Marks whether a room has been visited
        visited[0] = 1; // Start from room 0
        const queue = []; // JavaScript array used as a queue
        queue.push(0); // Start from room 0
        // Breadth-first search process
        while(queue.length !== 0){
            let key = queue[0];
            queue.shift();
            for(let k of rooms[key]){
                if(!visited[k]){
                    queue.push(k);
                    visited[k] = 1;
                }
            }
        }
        // Check if all rooms have been traversed
        for(let i of visited){
            if(i === 0) return false;
        }
        return true;
    }
    return bfs(rooms);
};

TypeScript

// BFS
// rooms: a directed graph represented by an adjacency list
// The core problem is, starting from 0, can all nodes be visited by a single traversal? Essentially a level order traversal.
function canVisitAllRooms(rooms: number[][]): boolean {
  const n = rooms.length;
  // cnt[i] represents the visitation order of node i, cnt[i] = 0 indicates it has not been visited.
  let cnt = new Array(n).fill(0);
  let queue = [0];
  cnt[0]++;
  while (queue.length > 0) {
    const from = queue.shift();
    for (let i = 0; i < rooms[from].length; i++) {
      const to = rooms[from][i];
      if (cnt[to] == 0) {
        queue.push(to);
        cnt[to]++;
      }
    }
  }
  // If any node has not been visited, return false
  return cnt.every((item) => item != 0);
}