827. Making A Large Island

LeetCode Link (opens new window)

You are given an n x n binary matrix grid. You can at most change one 0 to 1.

Return the largest island area in grid after you make that change.

An island is a group of 1s connected 4-directionally (horizontal or vertical).

Example 1:

• Input: grid = [[1, 0], [0, 1]]
• Output: 3
• Explanation: Change one 0 to 1, connecting two small islands to form an island of area 3.

Example 2:

• Input: grid = [[1, 1], [1, 0]]
• Output: 4
• Explanation: Change the 0 to 1 to expand the island area to 4.

Example 3:

• Input: grid = [[1, 1], [1, 1]]
• Output: 4
• Explanation: There is no 0 to change to 1, and the area remains 4.

Approach

One brute-force approach to this problem is to try changing every 0 on the map to 1, then search for the largest island area on the map.

To calculate the maximum area of an island: traverse the map and perform a depth-first search (DFS) on the island, with a time complexity of n * n.

(Actually, you can use either DFS or breadth-first search (BFS); both aim to traverse the island and make a mark, essentially "coloring" it, so any traversal method works. I'll explain using DFS below.)

By changing each 0, we need to re-calculate the maximum map area, resulting in an overall time complexity of n^4.

If you're not familiar with depth-first search, you can check it out here: Depth-first Search Theory (opens new window).

Optimization Approach

We actually do a lot of redundant work when using DFS iteratively to calculate the maximum island area.

We only need to record the area of each island once using DFS.

Step 1: Traverse the map once to find and record the size of each island with a unique identifier. We can use a map where the key is the island number and the value is the island area.

Step 2: Traverse the map again, inspecting 0s (as we want to change 0 to 1), summing the areas of adjacent islands, and then determine the maximum area after considering each 0.

Taking the island scenario on the map below as an example: (where 1 represents land)

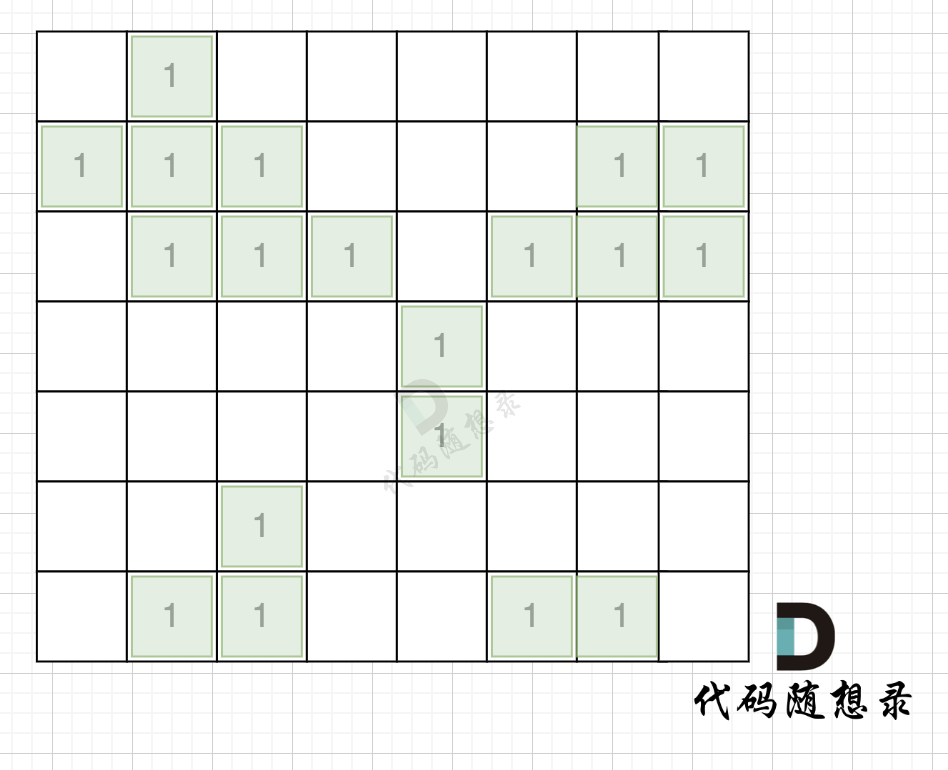
In the first step, traverse the map and collect statistics on island numbers and sizes as shown in the diagram below:

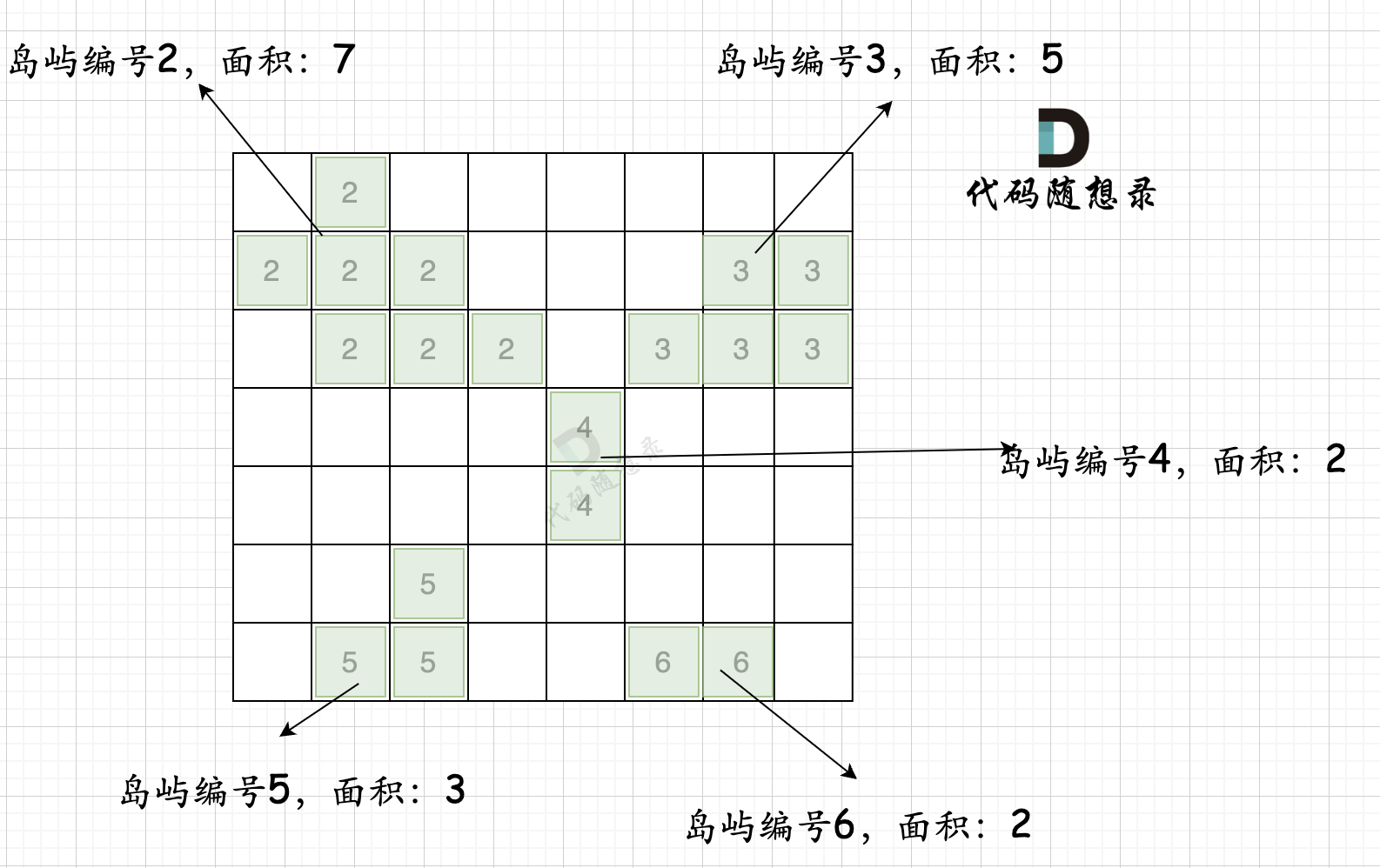
The code for this process is as follows:

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
    if (visited[x][y] || grid[x][y] == 0) return; // Termination condition: node already visited or encounter water
    visited[x][y] = true; // Mark as visited
    grid[x][y] = mark; // Assign a new label to the land
    count++;
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // Out of bounds, skip
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int largestIsland(vector<vector<int>>& grid) {
    int n = grid.size(), m = grid[0].size();
    vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // Mark visited points
    unordered_map<int, int> gridNum;
    int mark = 2; // Record each island's identifier
    bool isAllGrid = true; // Flag to check if the entire map is land
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) {
                count = 0;
                dfs(grid, visited, i, j, mark); // Mark all connected lands as true
                gridNum[mark] = count; // Record each island's area
                mark++; // Record the next island identifier
            }
        }
    }
}

This process has a time complexity of n * n. Some may wonder: it clearly seems like two nested loops with a dfs below; how does it end up as n * n?

If you look at the code closely, each node in the n * n grid is traversed only once and not repeatedly.

The second step process is illustrated in the diagram below:

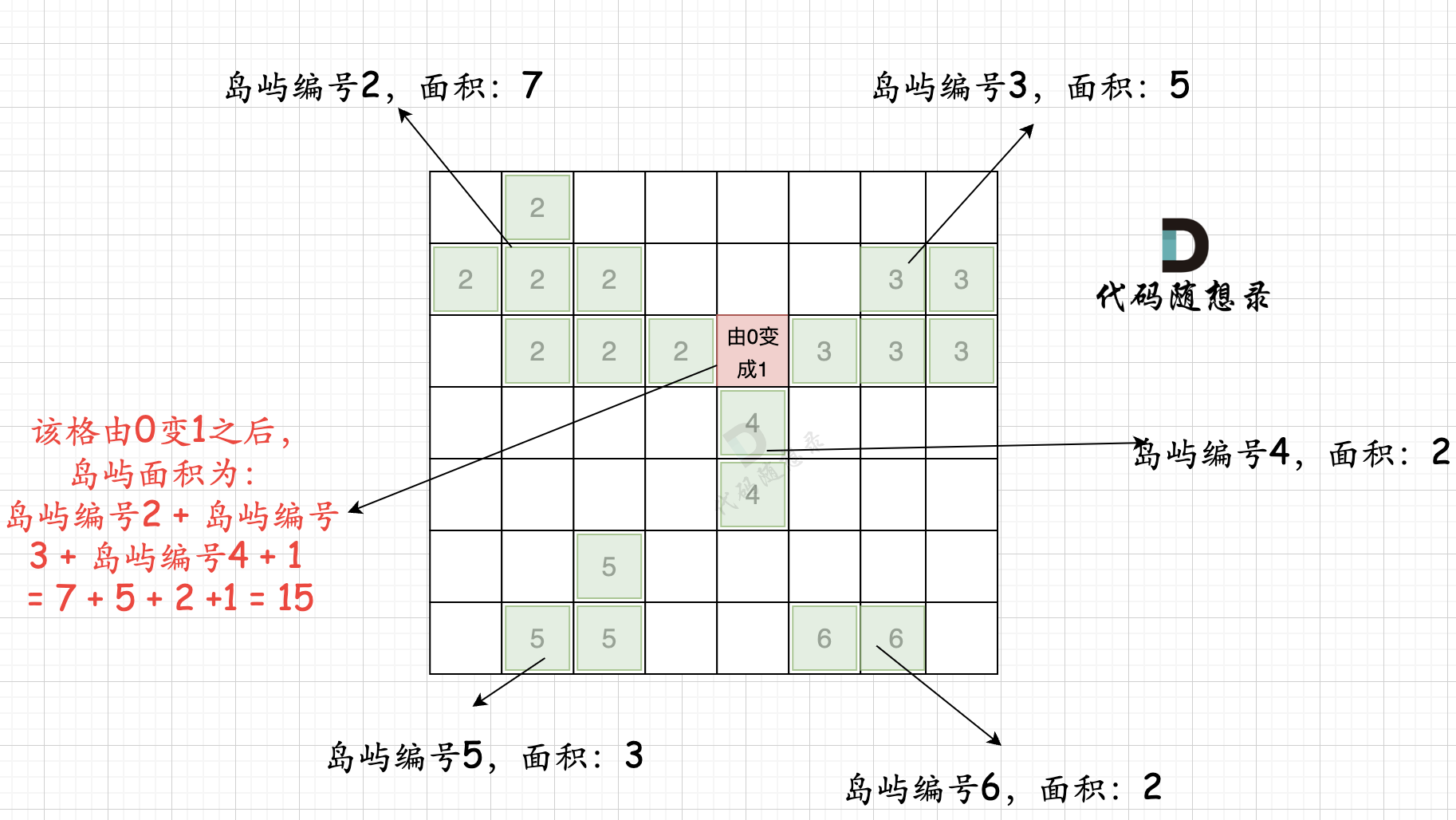
That is, for every 0 block, calculate the areas of its adjacent islands, sum them up, and finally get the maximum area after iterating through all 0s.

The process also has a time complexity of n * n.

So the overall solution has a time complexity of n * n + n * n, which is n^2.

Of course, there is another point for optimization: you don't need a visited array since you have mark for marking, so grid[i][j] that has been traversed will not be equal to 1.

The code is as follows:

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
void dfs(vector<vector<int>>& grid, int x, int y, int mark) {
    if (grid[x][y] != 1 || grid[x][y] == 0) return; // Termination condition: node already visited or encounter water
    grid[x][y] = mark; // Assign a new label to the land
    count++;
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // Out of bounds, skip
        dfs(grid, nextx, nexty, mark);
    }
}

int largestIsland(vector<vector<int>>& grid) {
    int n = grid.size(), m = grid[0].size();
    unordered_map<int ,int> gridNum;
    int mark = 2; // Record each island's identifier
    bool isAllGrid = true; // Flag to check if the entire map is land
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (grid[i][j] == 1) {
                count = 0;
                dfs(grid, i, j, mark); // Mark all connected lands as true
                gridNum[mark] = count; // Record each island's area
                mark++; // Record the next island identifier
            }
        }
    }
}

To maintain clarity among variables and ensure clean code, the complete code still uses a visited array for marking.

Finally, the complete code is as follows:

class Solution {
private:
    int count;
    int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
    void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
        if (visited[x][y] || grid[x][y] == 0) return; // Termination condition: node already visited or encounter water
        visited[x][y] = true; // Mark as visited
        grid[x][y] = mark; // Assign a new label to the land
        count++;
        for (int i = 0; i < 4; i++) {
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // Out of bounds, skip
            dfs(grid, visited, nextx, nexty, mark);
        }
    }

public:
    int largestIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // Mark visited points
        unordered_map<int, int> gridNum;
        int mark = 2; // Record each island's identifier
        bool isAllGrid = true; // Flag to check if the entire map is land
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 0) isAllGrid = false;
                if (!visited[i][j] && grid[i][j] == 1) {
                    count = 0;
                    dfs(grid, visited, i, j, mark); // Mark all connected lands as true
                    gridNum[mark] = count; // Record each island's area
                    mark++; // Record the next island identifier
                }
            }
        }
        if (isAllGrid) return n * m; // If all cells are land, return full area

        // The following logic calculates the sum of areas of adjacent islands based on the position of the added land
        int result = 0; // Record the final result
        unordered_set<int> visitedGrid; // Mark visited islands
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int count = 1; // Record the island count after the linkage
                visitedGrid.clear(); // Clear before each use
                if (grid[i][j] == 0) {
                    for (int k = 0; k < 4; k++) {
                        int neari = i + dir[k][1]; // Calculate adjacent coordinates
                        int nearj = j + dir[k][0];
                        if (neari < 0 || neari >= grid.size() || nearj < 0 || nearj >= grid[0].size()) continue;
                        if (visitedGrid.count(grid[neari][nearj])) continue; // Avoid adding the same island multiple times
                        // Sum up the size of adjacent islands
                        count += gridNum[grid[neari][nearj]];
                        visitedGrid.insert(grid[neari][nearj]); // Mark island as added
                    }
                }
                result = max(result, count);
            }
        }
        return result;
    }
};

Other Language Versions

Java

class Solution {
    private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};  // Four directions

    /**
     * @param grid The grid array
     * @param row The current row of the node being traversed
     * @param col The current column of the node being traversed
     * @param mark The current region's mark
     * @return The number of 1s in the current region
     */
    public int dfs(int[][] grid, int row, int col, int mark) {
        int ans = 0;
        grid[row][col] = mark;
        for (int[] current: position) {
            int curRow = row + current[0], curCol = col + current[1];
            if (curRow < 0 || curRow >= grid.length || curCol < 0 || curCol >= grid.length) continue;  // Out of bounds
            if (grid[curRow][curCol] == 1)
                ans += 1 + dfs(grid, curRow, curCol, mark);
        }
        return ans;
    }

    public int largestIsland(int[][] grid) {
        int ans = Integer.MIN_VALUE, size = grid.length, mark = 2;
        Map<Integer, Integer> getSize = new HashMap<>();
        for (int row = 0; row < size; row++) {
            for (int col = 0; col < size; col++) {
                if (grid[row][col] == 1) {
                    int areaSize = 1 + dfs(grid, row, col, mark);
                    getSize.put(mark++, areaSize);
                }
            }
        }
        for (int row = 0; row < size; row++) {
            for (int col = 0; col < size; col++) {
                // Skip the current position if it's not 0 since we can only change 0 to 1
                if (grid[row][col] != 0) continue;
                Set<Integer> hashSet = new HashSet<>();     // Prevent the same region from being counted multiple times
                // Calculate the number of 1s from the current position by default
                // because the 0 is turned into a 1
                int curSize = 1;
                for (int[] current: position) {
                    int curRow = row + current[0], curCol = col + current[1];
                    if (curRow < 0 || curRow >= grid.length || curCol < 0 || curCol >= grid.length) continue;
                    int curMark = grid[curRow][curCol];     // Get the mark of the corresponding position
                    // If the mark is already in hashSet, it means the mark has been recorded once
                    // If it doesn't exist in getSize, it means the mark is invalid (at this point curMark = 0)
                    if (hashSet.contains(curMark) || !getSize.containsKey(curMark)) continue;
                    hashSet.add(curMark);
                    curSize += getSize.get(curMark);
                }
                ans = Math.max(ans, curSize);
            }
        }
        // When ans == Integer.MIN_VALUE, it means there are no 0s in the grid, all are valid regions, return the size of the grid
        return ans == Integer.MIN_VALUE ? size * size : ans;
    }
}

Python

class Solution:
    def largestIsland(self, grid: List[List[int]]) -> int:
        visited = set()    # Mark visited positions
        m, n = len(grid), len(grid[0])
        res = 0
        island_size = 0     # Used to store the current island size
        directions = [[0, 1], [0, -1], [1, 0], [-1, 0]] # Four directions
        islands_size = defaultdict(int)  # Save the size of each island

        def dfs(island_num, r, c):
            visited.add((r, c))
            grid[r][c] = island_num     # Mark visited positions with island number
            nonlocal island_size
            island_size += 1
            for i in range(4):
                nextR = r + directions[i][0]
                nextC = c + directions[i][1]
                if (nextR not in range(m) or     # Row index out of bounds
                    nextC not in range(n) or     # Column index out of bounds
                    (nextR, nextC) in visited):  # Coordinate already visited
                    continue
                if grid[nextR][nextC] == 1:      # Encounter valid coordinate, go to the next level search
                    dfs(island_num, nextR, nextC)

        island_num = 2             # Initial island number set to 2, because grid data contains 0 and 1, so start numbering with 2
        all_land = True            # Flag to check if the entire map is land
        for r in range(m):
            for c in range(n):
                if grid[r][c] == 0:
                    all_land = False    # The map is not all land
                if (r, c) not in visited and grid[r][c] == 1:
                    island_size = 0     # Reset island size to 0 before traversing each position
                    dfs(island_num, r, c)
                    islands_size[island_num] = island_size # Save current island size
                    island_num += 1     # Move to the next island number
        if all_land:
            return m * n     # If all are land cells, return the map area

        count = 0            # Size of the current island after changing any 0 to 1
        # Since calculating island area needs to traverse in four directions, it's possible that the position in two or three directions may belong to the same island,
        # to avoid duplicate addition, add the already visited island number into this set.
        visited_island = set() # Save visited islands
        for r in range(m):
            for c in range(n):
                if grid[r][c] == 0:
                    count = 1        # Include the position where 0 is converted to 1 into the area
                    visited_island.clear()   # Clear set before traversing each position
                    for i in range(4):
                        nearR = r + directions[i][0]
                        nearC = c + directions[i][1]
                        if nearR not in range(m) or nearC not in range(n): # Surrounding positions out of bounds
                            continue
                        if grid[nearR][nearC] in visited_island:  # Island already visited
                            continue
                        count += islands_size[grid[nearR][nearC]] # Accumulate the area of adjacent islands
                        visited_island.add(grid[nearR][nearC])    # Mark current island as visited
                    res = max(res, count) 
        return res

Go

func largestIsland(grid [][]int) int {
	dir := [][]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}}
	n := len(grid)
	m := len(grid[0])
	area := 0
	visited := make([][]bool, n)
	for i := 0; i < n; i++ {
		visited[i] = make([]bool, m)
	}
	gridNum := make(map[int]int, 0) // Record the area of each island
	mark := 2                       // Record each island's identifier
	isAllGrid := true
	res := 0 // Flag to check if the entire map is land

	var dfs func(grid [][]int, visited [][]bool, x, y, mark int)
	dfs = func(grid [][]int, visited [][]bool, x, y, mark int) {
		// Termination condition: node already visited or encounter water
		if visited[x][y] || grid[x][y] == 0 {
			return
		}
		visited[x][y] = true // Mark as visited
		grid[x][y] = mark    // Assign a new label to the land
		area++
		for i := 0; i < 4; i++ {
			nextX := x + dir[i][0]
			nextY := y + dir[i][1]
			if nextX < 0 || nextX >= len(grid) || nextY < 0 || nextY >= len(grid[0]) {
				continue
			}
			dfs(grid, visited, nextX, nextY, mark)
		}
	}

	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			if grid[i][j] == 0 {
				isAllGrid = false
			}
			if !visited[i][j] && grid[i][j] == 1 {
				area = 0
				dfs(grid, visited, i, j, mark) // Mark all connected lands as true
				gridNum[mark] = area           // Record each island's area
				mark++                         // Update to the next island identifier
			}
		}
	}
	if isAllGrid {
		return n * m
	}
	// Based on the position of the added land, calculate the sum of adjacent island areas
	visitedGrid := make(map[int]struct{}) // Mark visited islands
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			count := 1                           // Record the island count after linkage
			visitedGrid = make(map[int]struct{}) // Clear before each use
			if grid[i][j] == 0 {
				for k := 0; k < 4; k++ {
					// Calculate adjacent coordinates
					nearI := i + dir[k][0]
					nearJ := j + dir[k][1]
					if nearI < 0 || nearI >= len(grid) || nearJ < 0 || nearJ >= len(grid[0]) {
						continue
					}
					// Skip already added islands
					if _, ok := visitedGrid[grid[nearI][nearJ]]; ok {
						continue
					}
					// Add up the size of adjacent islands
					count += gridNum[grid[nearI][nearJ]]
					// Mark the island as added
					visitedGrid[grid[nearI][nearJ]] = struct{}{}
				}
			}
			res = max827(res, count)
		}
	}
	return res
}

// Helper function to find max between two numbers
func max827(x, y int) int {
	if x > y {
		return x
	}
	return y
}

JavaScript

var largestIsland = function(grid) {
let res = 0;
const m = grid.length;
const n = grid[0].length;
const tag = new Array(n).fill().map(_ => new Array(m).fill(0));
const area = new Map();
const dir = [[0,1],[0,-1],[1,0],[-1,0]];
const dfs = (grid, tag, x, y, mark) => {
    let res = 1;
    tag[x][y] = mark;
    for(let i = 0; i < dir.length; i++) {
        let nextX = x + dir[i][0];
        let nextY = y + dir[i][1];
        if(nextX < 0 || nextX >= m || nextY < 0 || nextY >= n) {
            continue;
        }
        if(grid[nextX][nextY] === 1 && tag[nextX][nextY] === 0) {
            res += dfs(grid, tag, nextX, nextY, mark);
        }
    }
    return res;
}
let mark = 2;
// Assign mark to islands
for(let i = 0; i < m; i++) {      
    for(let j = 0; j < n; j++) {
        if(grid[i][j] === 1 && tag[i][j] === 0) {
            area.set(mark, dfs(grid, tag, i, j, mark));
            res = Math.max(res, area.get(mark));
            mark++;
        }
    }
}
// Change a non-island cell to land
for(let i = 0; i < m; i++) {
    for(let j = 0; j < n; j++) {
        if(grid[i][j] === 0) {
            let z = 1;
            const connected = new Set();
            for(let k = 0; k < dir.length; k++) {
                let nextX = i + dir[k][0];
                let nextY = j + dir[k][1];
                if(nextX < 0 || nextX >= m || nextY < 0 || nextY >= n || tag[nextX][nextY] === 0 || connected.has(tag[nextX][nextY])) {
                    continue;
                }
                z += area.get(tag[nextX][nextY]);
                connected.add(tag[nextX][nextY]);
            }
            res = Math.max(res, z);
        }
    }
}
return res;
};