# 787. Cheapest Flights Within K Stops

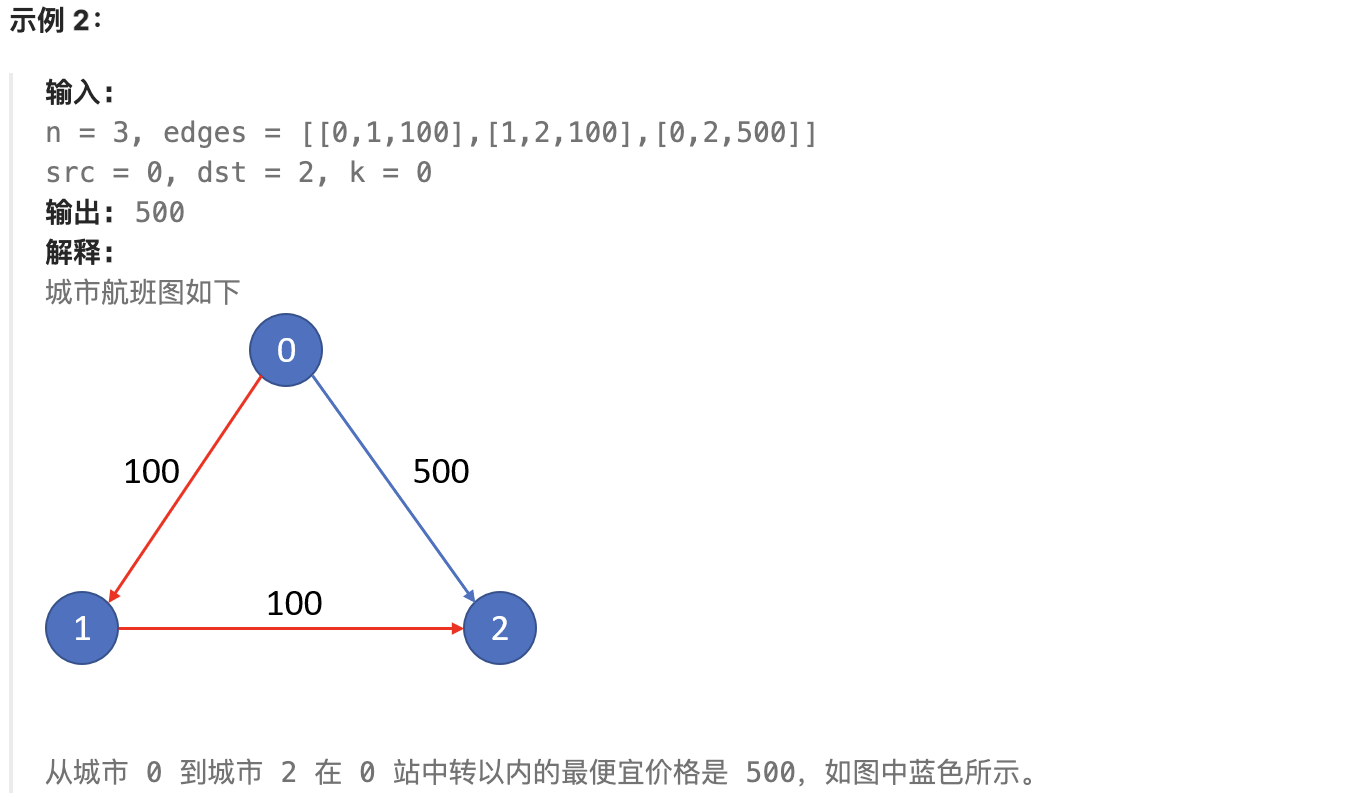
There are n cities connected by some flights. You are given an array flights, where flights[i] = [fromi, toi, pricei], representing a flight from city fromi to city toi with a price of pricei.

Now given all the cities and flights, as well as a starting city src and a destination city dst, your task is to find the route with at most k stops that results in the cheapest price from src to dst, and return that price. If no such route exists, return -1.

# Approach

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> minDist(n, INT_MAX/2);
        minDist[src] = 0;
        vector<int> minDist_copy(n); // Used to record the result of each iteration
        for (int i = 1; i <= k + 1; i++) {
            minDist_copy = minDist; // Get the results of the previous calculation
            for (auto &f : flights) {
                int from = f[0];
                int to = f[1];
                int price = f[2];
                minDist[to] = min(minDist_copy[from] + price, minDist[to]);
                // if (minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
            }

        }
        int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Below is a common wrong approach

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> minDist(n, INT_MAX/2);
        minDist[src] = 0;
        for (int i = 1; i <= k + 1; i++) {
            for (auto &f : flights) {
                int from = f[0];
                int to = f[1];
                int price = f[2];
                if (minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
            }
        }
        int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

SPFA

class Solution {
struct Edge {
    int to;  // Connected node
    int val; // Weight of the edge

    Edge(int t, int w): to(t), val(w) {}  // Constructor
};

public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> minDist(n, INT_MAX/2);
        vector<list<Edge>> grid(n + 1); // Adjacency list
        for (auto &f : flights) {
            int from = f[0];
            int to = f[1];
            int price = f[2];
            grid[from].push_back(Edge(to, price));
        }
        minDist[src] = 0;
        vector<int> minDist_copy(n); // Used to record the result of each iteration
        k++;
        queue<int> que;
        que.push(src);
        std::vector<bool> visited(n + 1, false); // Optional, improves efficiency by preventing repeated visits
        int que_size;
        while (k-- && !que.empty()) {

            minDist_copy = minDist; // Get the results of the previous calculation
            que_size = que.size();
            while (que_size--) { // This while loop design is really ingenious
                int node = que.front(); que.pop();
                for (Edge edge : grid[node]) {
                    int from = node;
                    int to = edge.to;
                    int price = edge.val;
                    if (minDist[to] > minDist_copy[from] + price) {
                        minDist[to] = minDist_copy[from] + price;
                        que.push(to);
                    }
                }

            }
        }
        int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

Queue with visited to prevent repeated visits

class Solution {
struct Edge {
    int to;  // Connected node
    int val; // Weight of the edge

    Edge(int t, int w): to(t), val(w) {}  // Constructor
};

public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> minDist(n, INT_MAX/2);
        vector<list<Edge>> grid(n + 1); // Adjacency list
        for (auto &f : flights) {
            int from = f[0];
            int to = f[1];
            int price = f[2];
            grid[from].push_back(Edge(to, price));
        }
        minDist[src] = 0;
        vector<int> minDist_copy(n); // Used to record the result of each iteration
        k++;
        queue<int> que;
        que.push(src);
        int que_size;
        while (k-- && !que.empty()) {
            // Note the position of this array
            vector<bool> visited(n + 1, false); // Optional, improves efficiency by preventing repeated access if the value is already calculated
            minDist_copy = minDist; // Get the results of the previous calculation
            que_size = que.size();
            while (que_size--) {
                int node = que.front(); que.pop();
                for (Edge edge : grid[node]) {
                    int from = node;
                    int to = edge.to;
                    int price = edge.val;
                    if (minDist[to] > minDist_copy[from] + price) {
                        minDist[to] = minDist_copy[from] + price;
                        if(visited[to]) continue; // No need to enqueue again, but need to calculate repeatedly, so placed here
                        visited[to] = true;
                        que.push(to);
                    }
                }

            }
        }
        int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49