685. Redundant Connection II

LeetCode Problem Link (opens new window)

In this problem, a rooted tree is a directed graph that satisfies the following conditions. The tree has only one root node, and all other nodes are successors of that root node. Every node except the root node has exactly one parent, while the root node has no parent.

Input a directed graph that consists of a tree with n nodes (node values are unique and range from 1 to n) and an additional directed edge. The additional edge consists of two different vertices within the range of 1 to n, and this additional edge is not part of the tree's existing edges.

The result graph is a 2D-array edges, where each element is a pair [ui, vi], indicating a directed edge from vertex ui to vertex vi, where ui is a parent of vi.

Return a removable edge such that the remaining graph is a rooted tree with n nodes. If there are multiple answers, return the answer that appears last in the given 2D-array.

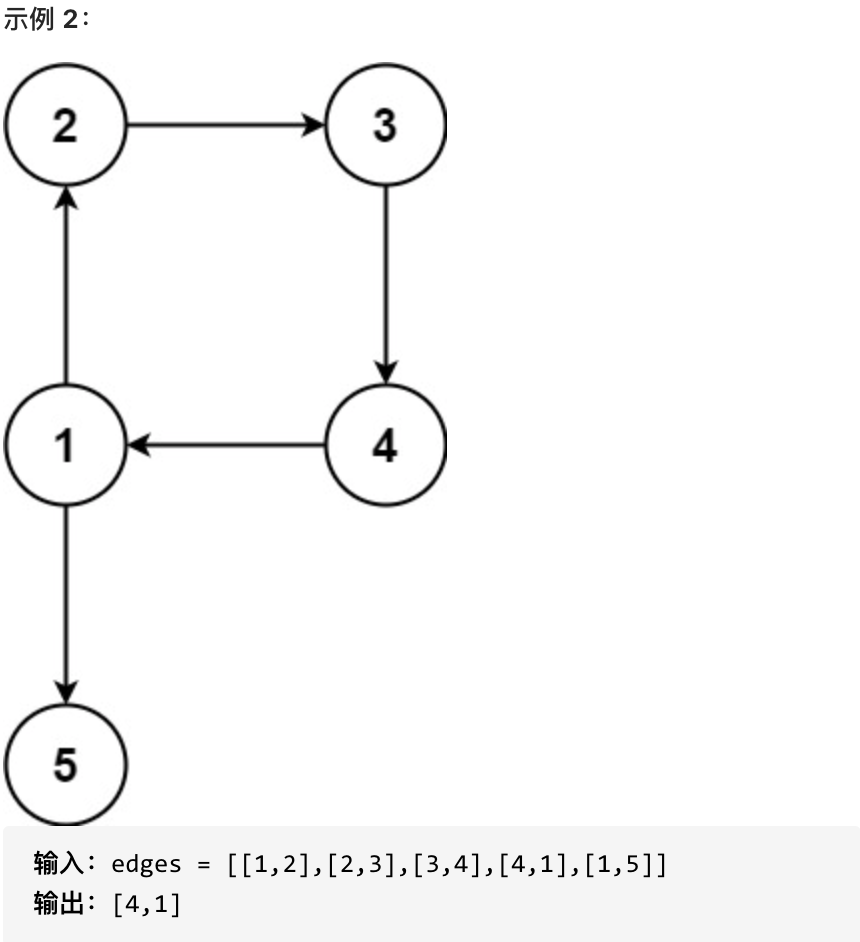
Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ui, vi <= n

Approach

First, focus on understanding this sentence in the problem: The graph consists of a tree with N nodes (nodes are uniquely numbered from 1 to N), and an additional edge. The endpoints of this additional edge are within the range of 1 to N, and this edge is not already present in the tree.

This implies that the graph in question was originally a tree, but with an additional edge added without increasing the number of nodes!

Also, if there are multiple solutions, return the one that appears last in the provided 2D-array. This implies that if there are two edges both of which can be removed to form a tree, the last one in sequence should be removed!

There are the following three cases. The first two involve a node with an in-degree of 2, as shown below:

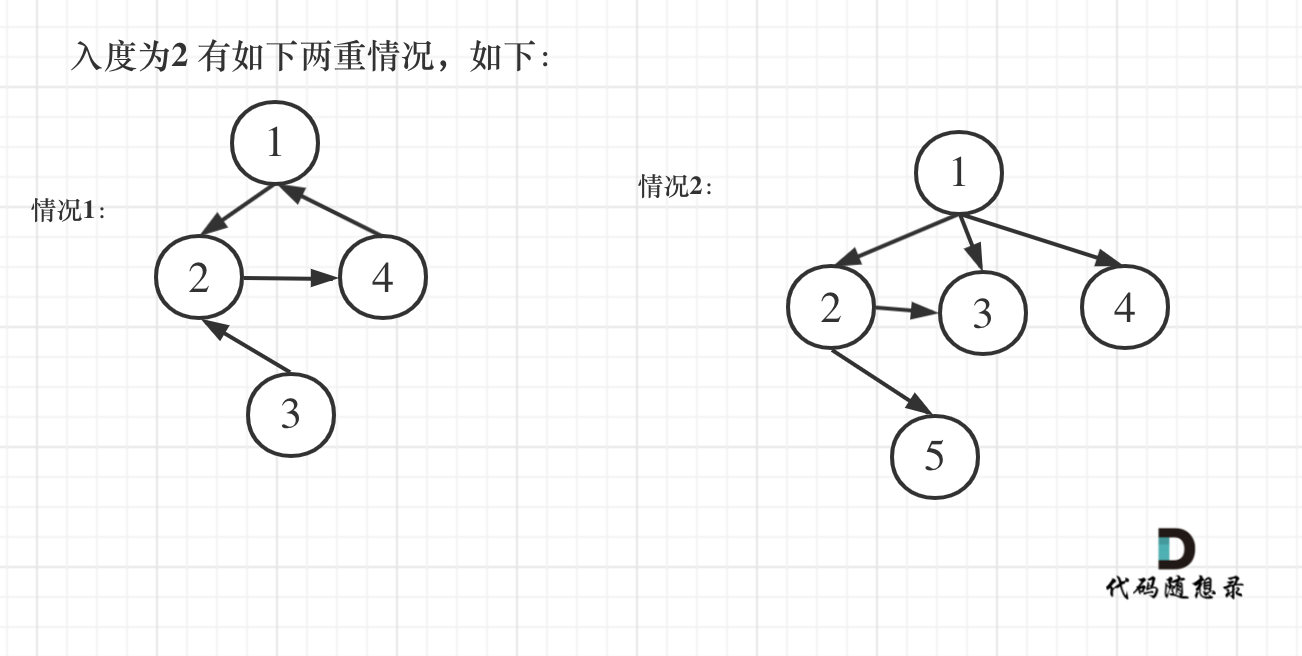
There is only one node with an in-degree of 2. Why not consider the out-degree? Out-degrees are irrelevant because any parent node in a tree naturally has multiple children.

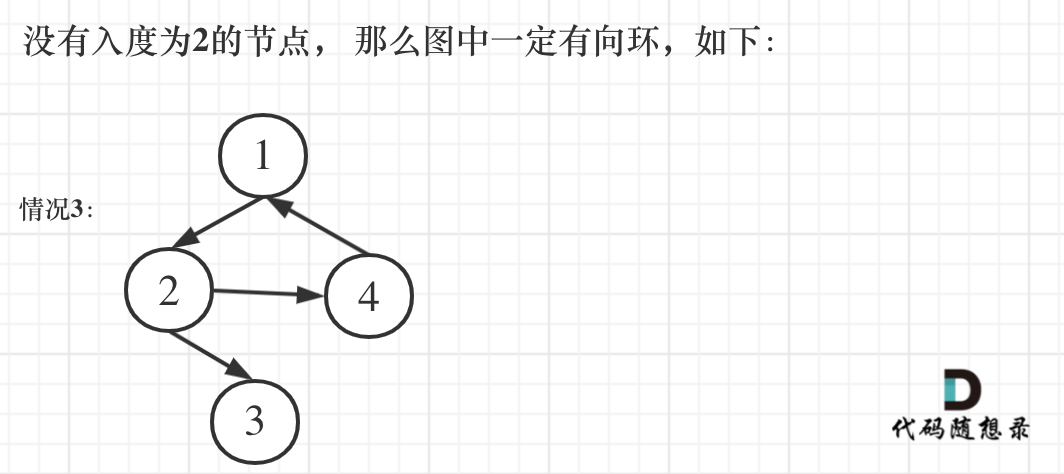
The third case is when there is no node with an in-degree of 2, which means there must be a directed cycle in the graph (note it's a directed cycle!)

Here's the representation:

First, calculate the in-degree of each node. Many often get confused when calculating the in-degree, unclear what edges[i][j] represents.

For example, if the given input is: edges = [[1,2],[1,3],[2,3]]

One might naturally think of the array as being: edges[1][2], edges[1][3], edges[2][3], but then wonder what the values of edges[1][2] actually mean. The more they think, the more confused they become.

In fact, edges = [[1,2],[1,3],[2,3]], means:

edges[0][0] = 1, edges[0][1] = 2,

edges[1][0] = 1, edges[1][1] = 3,

edges[2][0] = 2, edges[2][1] = 3.

2D arrays are something everyone learns, but when combined with graphs, it can be easy to mix up what are values and what are indices.

Once that's clear, how do we calculate the in-degree?

That is edges[i][1] denotes the node pointed to by an edge, indicating this node has an in-degree of one! (If you wanted to calculate the out-degree, it would be edges[i][0]).

The code to calculate in-degrees is as follows:

int inDegree[N] = {0}; // Record the in-degrees of nodes
n = edges.size(); // Number of edges
for (int i = 0; i < n; i++) {
    inDegree[edges[i][1]]++; // Calculate in-degree
}

For the first two cases with a node having an in-degree of 2, it must be one of the two edges pointing to this node that needs to be removed. If removing one makes the graph a tree, then that edge is the answer. Also, we iterate from back to front so that if two edges can both be removed, we remove the last one.

Here's the code:

vector<int> vec; // Store edges ending in a node with in-degree 2 (there will be two if this case occurs)
// Identify edges corresponding to nodes with in-degree 2, note the iteration is reverse due to return order of result
for (int i = n - 1; i >= 0; i--) {
    if (inDegree[edges[i][1]] == 2) {
        vec.push_back(i);
    }
}
// Handle cases 1 and 2
// If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
if (vec.size() > 0) {
    if (isTreeAfterRemoveEdge(edges, vec[0])) {
        return edges[vec[0]];
    } else {
        return edges[vec[1]];
    }
}

In case three, when there are no nodes with an in-degree of 2, there must be a directed cycle in the graph. Identify the edge forming the cycle which should be removed.

The code below defines this function:

// Find and remove the edge such that the graph becomes a tree; the return value is the edge to be removed
vector<int> getRemoveEdge(const vector<vector<int>>& edges)

You will then understand that we need to implement two critical functions:

• isTreeAfterRemoveEdge() which tests if removing one edge results in a tree.
• getRemoveEdge which assures there's a directed cycle in the graph and identifies the edge to be removed.

Now the union-find data structure comes into play. Why can union-find determine if a graph is a tree?

If the root of two vertices' edges can both be found in the union-find structure before adding any new edge, then this edge addition will ensure the graph is not a tree.

If you're not familiar with union-find, check Union-Find Theory Basics (opens new window).

Here is the full C++ code with ample comments:

class Solution {
private:
    static const int N = 1010; // Node ranges between 3 and 1000 as given in the problem
    int father[N];
    int n; // Number of edges

    // Initialize union-find structure
    void init() {
        for (int i = 1; i <= n; ++i) {
            father[i] = i;
        }
    }

    // Root finding process in union-find
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }

    // Add edge v->u to the union-find structure
    void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return;
        father[v] = u;
    }

    // Check if u and v have the same root
    bool same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    // Find and return the removable edge in the directed graph to make it a tree
    vector<int> getRemoveEdge(const vector<vector<int>>& edges) {
        init(); // Initialize the union-find structure
        for (int i = 0; i < n; i++) { // Iterate over all the edges
            if (same(edges[i][0], edges[i][1])) { // A directed cycle is found, indicating the edge to be removed
                return edges[i];
            }
            join(edges[i][0], edges[i][1]);
        }
        return {};
    }

    // Check if the graph becomes a tree after removing one edge
    bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {
        init(); // Initialize the union-find structure
        for (int i = 0; i < n; i++) {
            if (i == deleteEdge) continue;
            if (same(edges[i][0], edges[i][1])) { // A directed cycle is found, not a tree
                return false;
            }
            join(edges[i][0], edges[i][1]);
        }
        return true;
    }

public:

    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int inDegree[N] = {0}; // Record the in-degrees of nodes
        n = edges.size(); // Number of edges
        for (int i = 0; i < n; i++) {
            inDegree[edges[i][1]]++; // Calculate in-degree
        }
        vector<int> vec; // Record edges ending at a node with in-degree 2 (if exists, there are two)
        // Identify edges corresponding to nodes with in-degree 2, note the iteration is reverse due to return order of result
        for (int i = n - 1; i >= 0; i--) {
            if (inDegree[edges[i][1]] == 2) {
                vec.push_back(i);
            }
        }
        // Handle cases 1 and 2
        // If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
        if (vec.size() > 0) {
            if (isTreeAfterRemoveEdge(edges, vec[0])) {
                return edges[vec[0]];
            } else {
                return edges[vec[1]];
            }
        }
        // Handle case 3
        // If there are no nodes with in-degree 2, there must be a directed cycle, identify and return the edge forming it
        return getRemoveEdge(edges);

    }
};

Other Language Versions

Java

class Solution {

    private static final int N = 1010;  // Node ranges between 3 and 1000 as given in the problem
    private int[] father;
    public Solution() {
        father = new int[N];

        // Initialize union-find structure
        for (int i = 0; i < N; ++i) {
            father[i] = i;
        }
    }

    // Root finding process in union-find
    private int find(int u) {
        if (u == father[u]) {
            return u;
        }
        father[u] = find(father[u]);
        return father[u];
    }

    // Add edge v->u to the union-find structure
    private void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return;
        father[v] = u;
    }

    // Check if u and v have the same root, not utilized here
    private Boolean same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    /** 
     * Initialize the union-find structure.
     */
    private void initFather() {
        for (int i = 0; i < N; ++i) {
            father[i] = i;
        }
    }

    /**
     * Identify and return the removable edge in the directed graph to make it a tree.
     * @param edges
     * @return the edge to be removed.
     */
    private int[] getRemoveEdge(int[][] edges) {
        initFather();
        for (int i = 0; i < edges.length; i++) {
            if (same(edges[i][0], edges[i][1])) { // A directed cycle is found, indicating the edge to be removed
                return edges[i];
            }
            join(edges[i][0], edges[i][1]);
        }
        return null;
    }

    /** 
     * Check if the graph becomes a tree after removing one edge.
     * @param edges
     * @param deleteEdge the edge to be removed.
     * @return true if it becomes a tree, false otherwise.
     */
    private Boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge) {
        initFather();
        for (int i = 0; i < edges.length; i++) {
            if (i == deleteEdge) continue;
            if (same(edges[i][0], edges[i][1])) { // A directed cycle is found, not a tree
                return false;
            }
            join(edges[i][0], edges[i][1]);
        }
        return true;
    }

    public int[] findRedundantDirectedConnection(int[][] edges) {
        int[] inDegree = new int[N];
        for (int i = 0; i < edges.length; i++) {
            // Compute in-degrees
            inDegree[edges[i][1]] += 1;
        }

        // Identify edges corresponding to nodes with in-degree 2, note the iteration is reverse due to return order of result
        ArrayList<Integer> twoDegree = new ArrayList<>();
        for (int i = edges.length - 1; i >= 0; i--) {
            if (inDegree[edges[i][1]] == 2) {
                twoDegree.add(i);
            }
        }

        // Handle cases 1 and 2
        // If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
        if (!twoDegree.isEmpty()) {
            if (isTreeAfterRemoveEdge(edges, twoDegree.get(0))) {
                return edges[twoDegree.get(0)];
            }
            return edges[twoDegree.get(1)];
        }

        // Handle case 3
        // If there are no nodes with in-degree 2, there must be a directed cycle, identify and return the edge forming it
        return getRemoveEdge(edges);
    }
}

Python

class Solution:

    def __init__(self):
        self.n = 1010
        self.father = [i for i in range(self.n)]


    def find(self, u: int):
        """
        Root finding process in union-find
        """
        if u == self.father[u]:
            return u
        self.father[u] = self.find(self.father[u])
        return self.father[u]

    def join(self, u: int, v: int):
        """
        Add edge v->u to the union-find structure
        """
        u = self.find(u)
        v = self.find(v)
        if u == v: return
        self.father[v] = u
        pass


    def same(self, u: int, v: int):
        """
        Check if u and v have the same root
        """
        u = self.find(u)
        v = self.find(v)
        return u == v

    def init_father(self):
        self.father = [i for i in range(self.n)]
        pass

    def getRemoveEdge(self, edges: List[List[int]]) -> List[int]:
        """
        Identify and return the removable edge in the directed graph to make it a tree
        """

        self.init_father()
        for i in range(len(edges)):
            if self.same(edges[i][0], edges[i][1]):  # A directed cycle is found, indicating the edge to be removed
                return edges[i]
            self.join(edges[i][0], edges[i][1])
        return []

    def isTreeAfterRemoveEdge(self, edges: List[List[int]], deleteEdge: int) -> bool:
        """
        Check if the graph becomes a tree after removing one edge
        """

        self.init_father()
        for i in range(len(edges)):
            if i == deleteEdge: continue
            if self.same(edges[i][0], edges[i][1]):  # Directed cycle found, not a tree
                return False
            self.join(edges[i][0], edges[i][1])
        return True

    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        inDegree = [0] * self.n

        for i in range(len(edges)):
            inDegree[edges[i][1]] += 1

        # Identify edges corresponding to nodes with in-degree 2, reverse iteration for order of return
        twoDegree = []
        for i in range(len(edges))[::-1]:
            if inDegree[edges[i][1]] == 2:
                twoDegree.append(i)

        # Handle cases 1 and 2
        # If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
        if twoDegree:
            if self.isTreeAfterRemoveEdge(edges, twoDegree[0]):
                return edges[twoDegree[0]]
            return edges[twoDegree[1]]

        # Handle case 3
        # If there are no nodes with in-degree 2, there must be a directed cycle, identify and return the edge forming it
        return self.getRemoveEdge(edges)

Go

// Global definitions
var (
	n      = 1010 // Nodes range from 3 to 1000
	father = make([]int, n)
)

// Initialize union-find
func initialize() {
	for i := 0; i < n; i++ {
		father[i] = i
	}
}

// Root finding process in union-find
func find(u int) int {
	if u == father[u] {
		return u
	}
	father[u] = find(father[u])
	return father[u]
}

// Add edge v->u to the union-find structure
func join(u, v int) {
	u = find(u)
	v = find(v)
	if u == v {
		return
	}
	father[v] = u
}

// Check if u and v have the same root, not utilized here
func same(u, v int) bool {
	u = find(u)
	v = find(v)
	return u == v
}

// getRemoveEdge Identify and return the removable edge in the directed graph to make it a tree
func getRemoveEdge(edges [][]int) []int {
	initialize()
	for i := 0; i < len(edges); i++ { // Iterate over all the edges
		if same(edges[i][0], edges[i][1]) { // A directed cycle is found, indicating the edge to be removed
			return edges[i]
		}
		join(edges[i][0], edges[i][1])
	}
	return []int{}
}

// isTreeAfterRemoveEdge Check if the graph becomes a tree after removing one edge
func isTreeAfterRemoveEdge(edges [][]int, deleteEdge int) bool {
	initialize()
	for i := 0; i < len(edges); i++ {
		if i == deleteEdge {
			continue
		}
		if same(edges[i][0], edges[i][1]) { // Directed cycle found, not a tree
			return false
		}
		join(edges[i][0], edges[i][1])
	}
	return true
}

func findRedundantDirectedConnection(edges [][]int) []int {
	inDegree := make([]int, len(father))
	for i := 0; i < len(edges); i++ {
		// Compute in-degrees
		inDegree[edges[i][1]] += 1
	}
	// Store edges whose endpoints have in-degree 2 (only two in this case)
	// Identify edges corresponding to nodes with in-degree 2, note the iteration is reverse due to return order of result
	twoDegree := []int{}
	for i := len(edges) - 1; i >= 0; i-- {
		if inDegree[edges[i][1]] == 2 {
			twoDegree = append(twoDegree, i)
		}
	}

	// Handle cases 1 and 2
	// If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
	if len(twoDegree) > 0 {
		if isTreeAfterRemoveEdge(edges, twoDegree[0]) {
			return edges[twoDegree[0]]
		}
		return edges[twoDegree[1]]
	}

	// Handle case 3
	// If there are no nodes with in-degree 2, there must be a directed cycle, identify and return the edge forming it
	return getRemoveEdge(edges)
}

JavaScript

const N = 1010; // Nodes range from 3 to 1000
const father = new Array(N);
let n; // Number of edges

// Root finding process in union-find
const find = u => {
    return u == father[u] ? u : father[u] = find(father[u]);
};

// Add edge v->u to the union-find structure
const join = (u, v) => {
    u = find(u);
    v = find(v);
    if(u == v) return;
    father[v] = u;
};

// Check if u and v have the same root
const same = (u, v) => {
    u = find(u);
    v = find(v);
    return u == v;
};

// Identify and return the removable edge in the directed graph to make it a tree
const getRemoveEdge = edges => {
    // Initialize union-find
    for (let i = 1; i <= n; i++) {
        father[i] = i;
    }
    for (let i = 0; i < n; i++) { // Iterate over all edges
        if (same(edges[i][0], edges[i][1])) { // A directed cycle is found, indicating the edge to be removed
            return edges[i];
        }
        join(edges[i][0], edges[i][1]);
    }
    return [];
}

// Check if the graph becomes a tree after removing one edge
const isTreeAfterRemoveEdge = (edges, deleteEdge) => {
    // Initialize union-find
    for (let i = 1; i <= n; i++) {
        father[i] = i;
    }
    for (let i = 0; i < n; i++) {
        if (i == deleteEdge) continue;
        if (same(edges[i][0], edges[i][1])) { // Directed cycle found, not a tree
            return false;
        }
        join(edges[i][0], edges[i][1]);
    }
    return true;
}

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantDirectedConnection = function(edges) {
    n = edges.length; // Number of edges
    const inDegree = new Array(n + 1).fill(0); // Record node in-degrees
    for (let i = 0; i < n; i++) {
        inDegree[edges[i][1]]++; // Compute in-degrees
    }
    let vec = []; // Store edges ending in nodes with in-degree 2 (there will be two if this case exists)
    // Identify edges corresponding to nodes with in-degree 2, note the iteration is reverse due to return order of result
    for (let i = n - 1; i >= 0; i--) {
        if (inDegree[edges[i][1]] == 2) {
            vec.push(i);
        }
    }
    // Handle cases 1 and 2
    // If a node with in-degree 2 exists, one of its edges needs to be deleted to form a tree
    if (vec.length > 0) {
        if (isTreeAfterRemoveEdge(edges, vec[0])) {
            return edges[vec[0]];
        } else {
            return edges[vec[1]];
        }
    }
    // Handle case 3
    // If there are no nodes with in-degree 2, there should be a directed cycle; identify and return the edge forming it
    return getRemoveEdge(edges);
};