684. Redundant Connection

LeetCode Problem Link (opens new window)

A tree is a connected, acyclic, undirected graph.

Given a graph formed by adding an edge to a tree with n nodes (with node values between 1 and n), where the added edge's endpoints are included within 1 to n, and the graph doesn't currently include this edge. The graph's information is recorded in a 2D array edges, where edges[i] = [ai, bi] represents an edge between nodes ai and bi.

Please find an edge that can be removed, making the remaining graph a tree with n nodes. If there are multiple answers, return the last specified edge in the array edges.

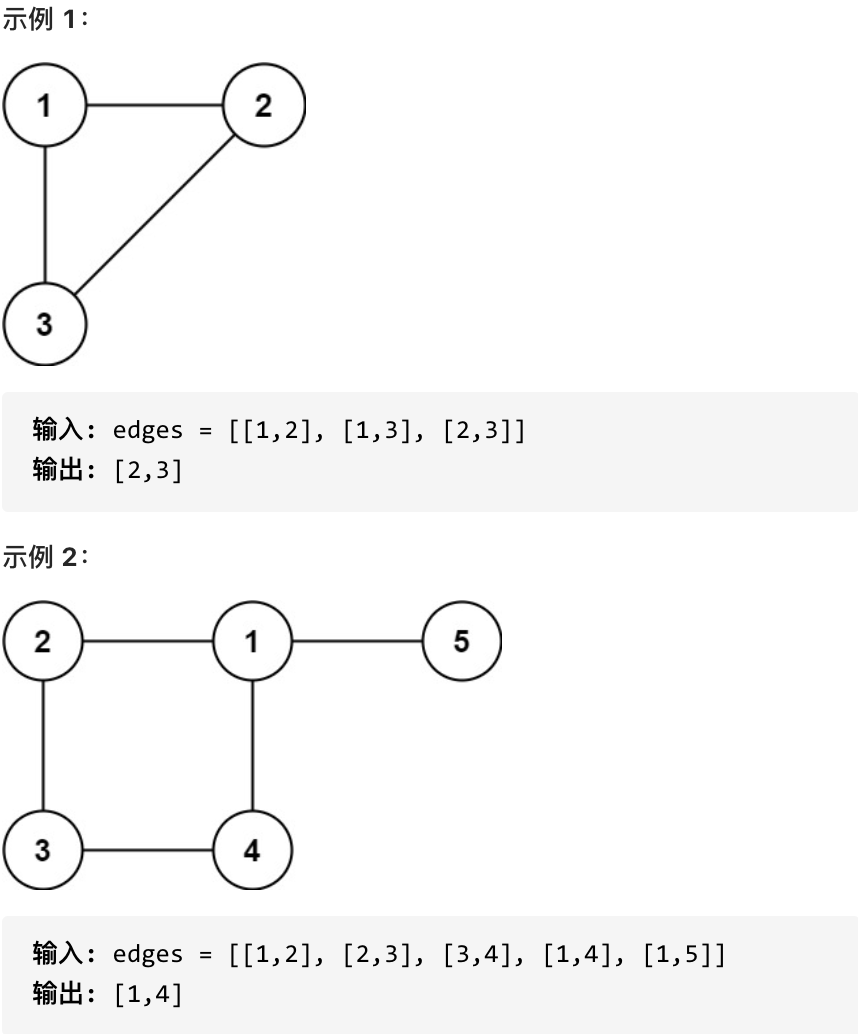
Hints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges contains no duplicate elements
• The given graph is connected

Approach

This problem is a fundamental example of using Union-Find.

Firstly, what can the union-find data structure help solve?

It's mainly used for the problem of finding sets: determining if two nodes are in the same set, or joining two nodes into the same set.

Here's a template of my union-find structure:

int n = 1005; // n is determined based on the number of nodes in the problem. It should generally be slightly larger than the number of nodes.
vector<int> father = vector<int> (n, 0); // An array structure in C++

 // Initialize union-find
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}

// The process of finding the root in union-find
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // Path compression
}

// Check if u and v have the same root
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// Add the edge v->u to the union-find
void join(int u, int v) {
    u = find(u); // Find the root of u
    v = find(v); // Find the root of v
    if (u == v) return ; // If the roots are the same, it means they're already in one set, so no need to connect the two nodes. Just return.
    father[v] = u;
}

In the above template, you just need to modify n. In this problem, the number of nodes won't exceed 1000.

The union-find mainly has three functionalities:

1. Find the root node, function: find(int u), which determines the ancestor node of this node.
2. Add two nodes into the same set, function: join(int u, int v), which connects two nodes to the same root node.
3. Determine if two nodes are in the same set, function: isSame(int u, int v), which checks if two nodes have the same root node.

For more foundational knowledge on union-find, please refer to this: Union-Find Basics (opens new window).

Now, let's take a look at this problem.

The problem states it's an undirected graph, and you need to return an edge to be removed, so that the resulting graph is a tree with N nodes (i.e., it has only one root node).

If there are multiple answers, then return the last specified edge in the 2D array.

We can iterate through each edge from the start (since there's a preference to connect earlier edges), if the two nodes of an edge are not in the same set, add them to a set (i.e., the same root node).

As shown in the diagram:

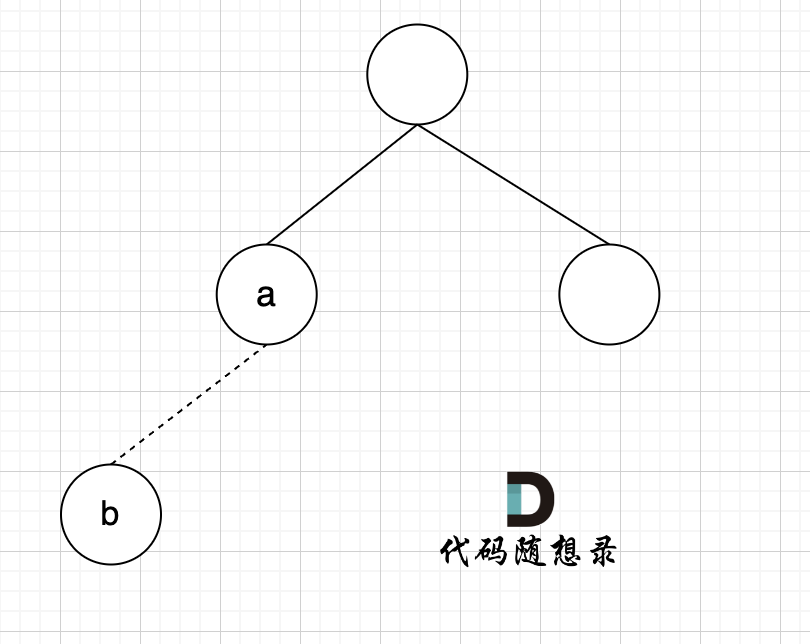
Nodes A and B are not in the same set, so they can be connected.

(If the problem states: If there are multiple answers, return the earliest appearing edge in the 2D array. Then we would iterate from the end to the start).

If the two nodes of an edge are already in the same set, this means the two nodes are already connected, and adding this edge will definitely create a loop.

As shown in the diagram:

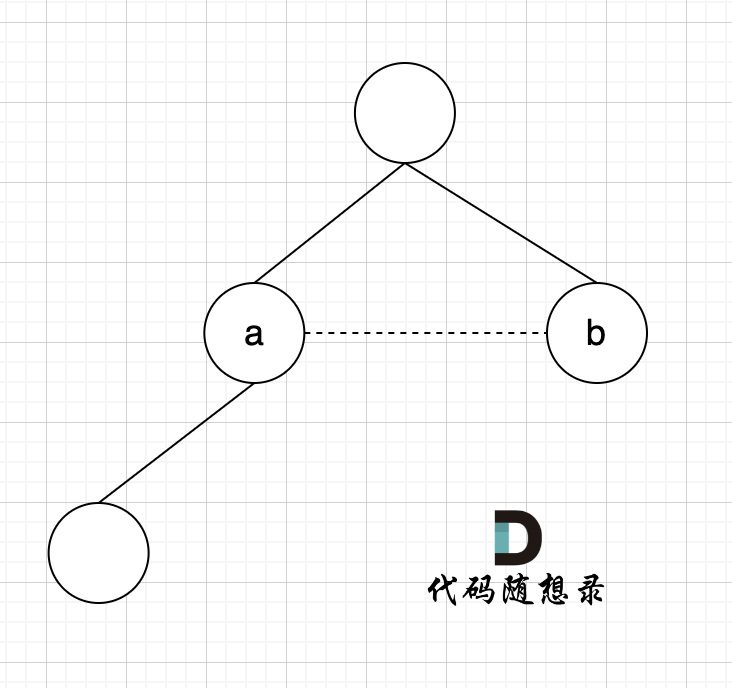
It has been determined that nodes A and B are in the same set (same root), and connecting node A and node B together will definitely create a loop.

With this clear thought process, the code is easy to write.

C++ code for union-find is as follows:

class Solution {
private:
    int n = 1005; // Number of nodes from 3 to 1000
    vector<int> father = vector<int> (n, 0); // An array structure in C++

    // Initialize union-find
    void init() {
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }

    // The process of finding the root in union-find
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }

    // Check if u and v have the same root
    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    // Add the edge v->u to the union-find
    void join(int u, int v) {
        u = find(u); // Find the root of u
        v = find(v); // Find the root of v
        if (u == v) return ; // If the roots are the same, it means they're already in one set, so no need to connect the two nodes. Just return.
        father[v] = u;
    }

public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        init();
        for (int i = 0; i < edges.size(); i++) {
            if (isSame(edges[i][0], edges[i][1])) return edges[i];
            else join(edges[i][0], edges[i][1]);
        }
        return {};
    }
};

As you can see, there's very little code in the main function, just checking if the two nodes of an edge are in the same set.

Other Language Versions

Java

class Solution {
    private int n;  // Number of nodes from 3 to 1000
    private int[] father;
    public Solution() {
        n = 1005;
        father = new int[n];

        // Initialize union-find
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }

    // The process of finding the root in union-find
    private int find(int u) {
        if(u == father[u]) {
            return u;
        }
        father[u] = find(father[u]);
        return father[u];
    }

    // Add the edge v->u to the union-find
    private void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return ;
        father[v] = u;
    }

    // Check if u and v have the same root, not used in this problem
    private Boolean same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    public int[] findRedundantConnection(int[][] edges) {
        for (int i = 0; i < edges.length; i++) {
            if (same(edges[i][0], edges[i][1])) {
                return edges[i];
            } else  {
                join(edges[i][0], edges[i][1]);
            }
        }
        return null;
    }
}

Python

class Solution:
    def __init__(self):
        """
        Initialize
        """
        self.n = 1005
        self.father = [i for i in range(self.n)]

    def find(self, u):
        """
        The process of finding the root in union-find
        """
        if u == self.father[u]:
            return u
        self.father[u] = self.find(self.father[u])
        return self.father[u]

    def join(self, u, v):
        """
        Add the edge v->u to the union-find
        """
        u = self.find(u)
        v = self.find(v)
        if u == v : return
        self.father[v] = u
        pass

    def same(self, u, v ):
        """
        Check if u and v have the same root, not used in this problem
        """
        u = self.find(u)
        v = self.find(v)
        return u == v

    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        for i in range(len(edges)):
            if self.same(edges[i][0], edges[i][1]) :
                return edges[i]
            else :
                self.join(edges[i][0], edges[i][1])
        return []

Simplified Python Version:

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        p = [i for i in range(n+1)]
        def find(i):
            if p[i] != i:
                p[i] = find(p[i])
            return p[i]
        for u, v in edges:
            if p[find(u)] == find(v):
                return [u, v]
            p[find(u)] = find(v)

Go

// Global variables
var (
    n = 1005 // Number of nodes from 3 to 1000
    father = make([]int, 1005)
)

// Initialize union-find
func initialize() {
	for i := 0; i < n; i++ {
		father[i] = i
	}
}

// The process of finding the root in union-find
func find(u int) int {
	if u == father[u] {
		return u
	}
	father[u] = find(father[u])
	return father[u]
}

// Add the edge v->u to the union-find
func join(u, v int) {
	u = find(u)
	v = find(v)
	if u == v {
		return
	}
	father[v] = u
}

// Check if u and v have the same root, not used in this problem
func same(u, v int) bool {
	u = find(u)
	v = find(v)
	return u == v
}

func findRedundantConnection(edges [][]int) []int {
	initialize()
	for i := 0; i < len(edges); i++ {
		if same(edges[i][0], edges[i][1]) {
			return edges[i]
		} else {
			join(edges[i][0], edges[i][1])
		}
	}
	return []int{}
}

JavaScript

const n = 1005;
const father = new Array(n);
// The process of finding the root in union-find
const find = u => {
    return u == father[u] ? u : father[u] = find(father[u]);
};

// Add the edge v->u to the union-find
const join = (u, v) => {
    u = find(u);
    v = find(v);
    if(u == v) return;
    father[v] = u;
};

// Check if u and v have the same root, not used in this problem
const same = (u, v) => {
    u = find(u);
    v = find(v);
    return u == v;
};

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function(edges) {
    // Initialize union-find
    for(let i = 0; i < n; i++){
        father[i] = i;
    }
    for(let i = 0; i < edges.length; i++){
        if(same(edges[i][0], edges[i][1])) return edges[i];
        else join(edges[i][0], edges[i][1]);
    }
    return null;
};