# 200. Number of Islands
Problem Link (opens new window)
Given a 2D grid, consisting of '1' (land) and '0' (water), please calculate the number of islands in the grid.
An island is surrounded by water and is formed by connecting adjacent lands horizontally and/or vertically.
Additionally, you can assume that all four edges of the grid are surrounded by water.

Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 300
- grid[i][j] is either '0' or '1'
# Approach
Pay attention to the condition stating that each island can only be formed by connecting adjacent lands horizontally and/or vertically.
This means diagonal connections are not counted. For example, in the second example, there are three islands, as shown:
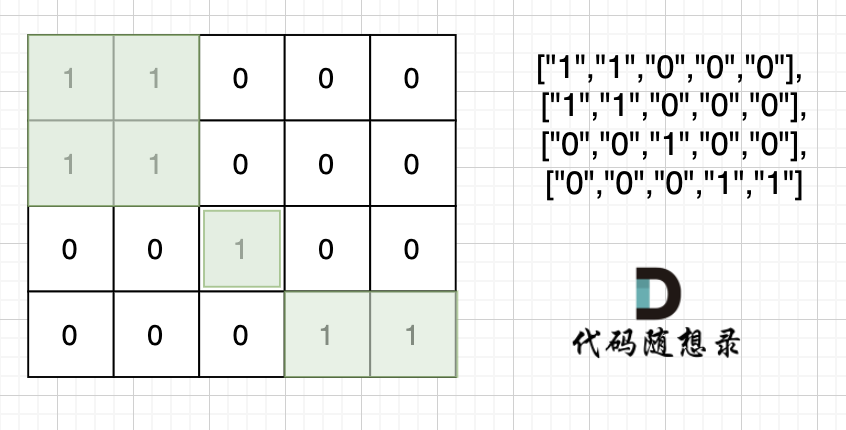
This problem can be solved using DFS, BFS, or Union-Find as a foundational problem.
The solution approach involves encountering an unexplored land node and incrementing the counter. Then, mark all the lands reachable from this node.
Skip over marked land nodes and water nodes. This way, the counter will represent the final count of islands.
To mark all the lands from a given node, you can use DFS, BFS, or Union-Find.
# Depth-First Search
The following code uses DFS. If you are not familiar with DFS, it is suggested to first read this article: 797. All Paths From Source to Target (opens new window).
C++ code is as follows:
// Version 1
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // Out of bounds, skip
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // Explore unvisited land
visited[nextx][nexty] = true;
dfs(grid, visited, nextx, nexty);
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
visited[i][j] = true;
result++; // Increment for an unvisited land
dfs(grid, visited, i, j); // Mark all connected lands as visited
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Many might wonder why there is no termination condition for the dfs function in the above code. It might seem risky without termination in recursion.
Actually, the termination condition is handled where dfs is called. If a direction is invalid, dfs isn't invoked.
You can also write it this way:
// Version 2
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // Four directions
void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y] || grid[x][y] == '0') return; // Termination: visited node or water
visited[x][y] = true; // Mark as visited
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // Out of bounds, skip
dfs(grid, visited, nextx, nexty);
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
result++; // Increment for an unvisited land
dfs(grid, visited, i, j); // Mark all connected lands as visited
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
The difference between the two versions should be clear: In version 1, the call to dfs is only done for valid nodes, thus called only with valid nodes.
In version 2, it performs dfs regardless and checks for validity and returns if invalid during recursion.
Theoretically, version 1 is more efficient because it avoids unnecessary recursive calls by checking the conditions before calling dfs. But version 2 might be more intuitive. (There's not a huge difference, though)
Many people might notice that even with the same DFS problem, the implementations might differ, some with termination conditions, some without. This is the root cause—two different ways of writing it.
# Summary
Although this is a template problem for DFS and BFS, there are many intricate details that often get overlooked. I have highlighted all such important details that can be pitfalls later.
For now, I've provided the DFS implementation. If you find that I've explained it in detail, later I'll present the BFS solution as well. Despite being a template, there are still noteworthy points to discuss. Stay tuned!
# Other Language Versions
# Java
The following code uses Depth First Search (DFS). To count the number of islands without recording them multiple times, whenever an island is detected, we "sink" it — which means changing the island's cells from '1' to '0'. This ensures no repeated counting of islands. The DFS step effectively performs this "sinking". See code below:
public int numIslands(char[][] grid) {
int res = 0; // Counter for the number of discovered islands
for(int i = 0;i < grid.length;i++){
for(int j = 0;j < grid[0].length;j++){
// Discover a "1", increment res, and sink the island
if(grid[i][j] == '1'){
res++;
dfs(grid,i,j);
}
}
}
return res;
}
// Use DFS to "sink" an island
public void dfs(char[][] grid, int i, int j){
// Search boundary: index out of bounds or reaching "0"
if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0') return;
// Mark this land as "0"
grid[i][j] = '0';
// According to "Each island is formed by connecting adjacent lands horizontally or vertically", perform DFS on the adjacent vertices in the four directions
dfs(grid,i - 1,j);
dfs(grid,i + 1,j);
dfs(grid,i,j + 1);
dfs(grid,i,j - 1);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Graph - DFS (consistent with Carl's code logic)
class Solution {
boolean[][] visited;
int dir[][] = {
{0, 1}, //right
{1, 0}, //down
{-1, 0}, //up
{0, -1} //left
};
public int numIslands(char[][] grid) {
int count = 0;
visited = new boolean[grid.length][grid[0].length];
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(visited[i][j] == false && grid[i][j] == '1'){
count++;
dfs(grid, i, j);
}
}
}
return count;
}
private void dfs(char[][]grid, int x, int y){
if(visited[x][y] == true || grid[x][y] == '0')
return;
visited[x][y] = true;
for(int i = 0; i < 4; i++){
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
continue;
dfs(grid, nextX, nextY);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Python:
# Version 1
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
visited = [[False] * n for _ in range(m)]
dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)] # Four directions
result = 0
def dfs(x, y):
for d in dirs:
nextx = x + d[0]
nexty = y + d[1]
if nextx < 0 or nextx >= m or nexty < 0 or nexty >= n: # Out of bounds, skip
continue
if not visited[nextx][nexty] and grid[nextx][nexty] == '1': # Unvisited land
visited[nextx][nexty] = True
dfs(nextx, nexty)
for i in range(m):
for j in range(n):
if not visited[i][j] and grid[i][j] == '1':
visited[i][j] = True
result += 1 # Increment for an unvisited land
dfs(i, j) # Mark all connected lands as visited
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Version 2
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
visited = [[False] * n for _ in range(m)]
dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)] # Four directions
result = 0
def dfs(x, y):
if visited[x][y] or grid[x][y] == '0':
return # Termination: visited node or water
visited[x][y] = True
for d in dirs:
nextx = x + d[0]
nexty = y + d[1]
if nextx < 0 or nextx >= m or nexty < 0 or nexty >= n: # Out of bounds, skip
continue
dfs(nextx, nexty)
for i in range(m):
for j in range(n):
if not visited[i][j] and grid[i][j] == '1':
result += 1 # Increment for an unvisited land
dfs(i, j) # Mark all connected lands as visited
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# We will use three states to mark each cell
# 0 indicates water
# 1 indicates land
# 2 indicates visited land
class Solution:
def traversal(self, grid, i, j):
m = len(grid)
n = len(grid[0])
if i < 0 or j < 0 or i >= m or j >= n:
return # Out of bounds
elif grid[i][j] == "2" or grid[i][j] == "0":
return
grid[i][j] = "2"
self.traversal(grid, i - 1, j) # Move up
self.traversal(grid, i + 1, j) # Move down
self.traversal(grid, i, j - 1) # Move left
self.traversal(grid, i, j + 1) # Move right
def numIslands(self, grid: List[List[str]]) -> int:
res = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == "1":
res += 1
self.traversal(grid, i, j)
return res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# JavaScript
var numIslands = function (grid) {
let dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]; // Four directions
let dfs = (grid, visited, x, y) => {
for (let i = 0; i < 4; i++) {
let nextX = x + dir[i][0]
let nextY = y + dir[i][1]
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length)
continue;
if (!visited[nextX][nextY] && grid[nextX][nextY] === "1") {
visited[nextX][nextY] = true
dfs(grid,visited,nextX,nextY)
}
}
}
let visited = new Array(grid.length).fill().map(() => Array(grid[0].length).fill(false))
let res = 0
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[i].length; j++) {
if (!visited[i][j] && grid[i][j] === "1") {
++res;
visited[i][j] = true;
dfs(grid, visited, i, j);
}
}
}
return res
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# TypeScript
function numIslands(grid: string[][]): number {
// Four directions
const dir: number[][] = [[0, 1], [1, 0], [-1, 0], [0, -1]];
const [m, n]: [number, number] = [grid.length, grid[0].length];
function dfs(grid: string[][], visited: boolean[][], x: number, y: number) {
for (let i = 0; i < 4; i++) {
let nextX: number = x + dir[i][0];
let nextY: number = y + dir[i][1];
// Out of bounds, skip
if (nextX < 0 || nextX >= m || nextY < 0 || nextY >= n) {
continue;
}
// Unvisited and is land
if (!visited[nextX][nextY] && grid[nextX][nextY] === '1') {
visited[nextX][nextY] = true;
dfs(grid, visited, nextX, nextY);
}
}
}
const visited: boolean[][] = Array.from({ length: m }, _ => new Array(n).fill(false));
let result: number = 0;
for (let i = 0; i < m; i++) {
for (let k = 0; k < n; k++) {
if (!visited[i][k] && grid[i][k] === '1') {
++result; // Increment for an unvisited land
visited[i][k] = true;
dfs(grid, visited, i, k); // Mark all connected lands as visited
}
}
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Go
var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
func numIslands(grid [][]byte) int {
res := 0
visited := make([][]bool, len(grid))
for i := 0; i < len(grid); i++ {
visited[i] = make([]bool, len(grid[0]))
}
for i, rows := range grid {
for j, v := range rows {
if v == '1' && !visited[i][j] {
res++
dfs(grid, visited, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, visited [][]bool, i, j int) {
visited[x][y] = true
for _, d := range DIRECTIONS {
x, y := i+d[0], j+d[1]
if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
continue
}
if grid[x][y] == '1' && !visited[x][y] {
dfs(grid, visited, x, y)
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Rust:
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn num_islands(grid: Vec<Vec<char>>) -> i32 {
let mut visited = vec![vec![false; grid[0].len()]; grid.len()];
let mut res = 0;
for (i, chars) in grid.iter().enumerate() {
for (j, &c) in chars.iter().enumerate() {
if !visited[i][j] && c == '1' {
res += 1;
Self::dfs(&grid, &mut visited, (i as i32, j as i32));
}
}
}
res
}
pub fn dfs(grid: &Vec<Vec<char>>, visited: &mut Vec<Vec<bool>>, (x, y): (i32, i32)) {
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (x + dx, y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
let (nx, ny) = (nx as usize, ny as usize);
if grid[nx][ny] == '1' && !visited[nx][ny] {
visited[nx][ny] = true;
Self::dfs(grid, visited, (nx as i32, ny as i32));
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
