141. Linked List Cycle

LeetCode Problem Link (opens new window)

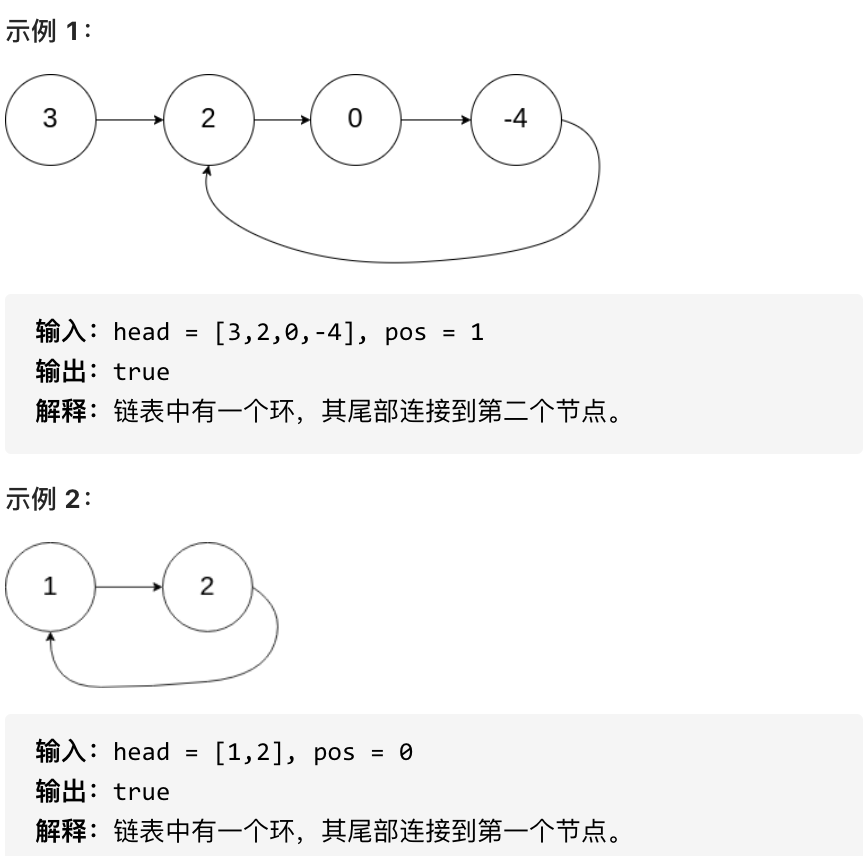
Given a linked list, determine if it has a cycle in it.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the list where the tail connects back into. If pos is -1, then there is no cycle in the linked list. Note that pos is not passed as a parameter, it is only there to represent the actual situation of the linked list.

Return true if there is a cycle in the linked list. Otherwise, return false.

Approach

You can use the fast and slow pointer technique. Define both fast and slow pointers that start from the head node. The fast pointer moves forward by two nodes each step, while the slow pointer moves forward by one node each step. If there is a cycle, the fast and slow pointers will meet at some point within the cycle.

Why do the fast and slow pointers meet within the cycle, instead of missing each other indefinitely?

Firstly, the fast pointer will definitely enter the cycle first. If the fast and slow pointers meet, it will certainly be within the cycle, which is undeniable.

So, why do the fast and slow pointers definitely meet?

You can draw a cycle and start the fast pointer at any node to chase the slow pointer. You will find that eventually, they converge as shown below:

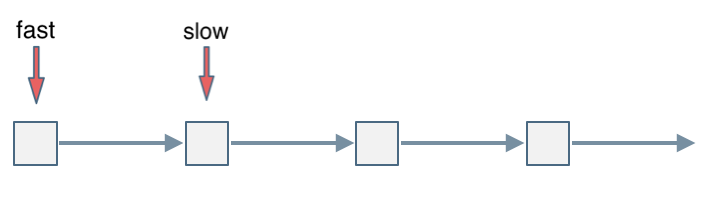
After both the fast and slow pointers take one more step, they meet.

This is because the fast pointer moves two nodes while the slow pointer moves one node. Relative to the slow pointer, the fast pointer is closing in one node at a time, so they will inevitably coincide.

Here is the animation:

The C++ code is as follows:

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            // If fast and slow pointers meet, there is a cycle
            if (slow == fast) return true;
        }
        return false;
    }
};

Further Exploration

After solving this problem, you can try Linked List Cycle II (opens new window), which not only requires finding the cycle but also locating the cycle's entry point.

Other Language Versions

Java:

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        // A null list or a single node list will definitely not have a cycle
        while (fast != null && fast.next != null) {
            fast = fast.next.next; // Fast pointer, moving two steps at a time
            slow = slow.next;      // Slow pointer, moving one step at a time
            if (fast == slow) {    // If fast and slow pointers meet, there is a cycle
                return true;
            }
        }
        return false; // Reached the end of the list normally, indicating no cycle
    }
}

Python:

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if not head: return False
        slow, fast = head, head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if fast == slow:
                return True
        return False

Go:

func hasCycle(head *ListNode) bool {
    if head==nil{
        return false
    } // an empty list will definitely not have a cycle
    fast := head
    slow := head // Fast and slow pointers
    for fast.Next!=nil && fast.Next.Next!=nil {
        fast = fast.Next.Next
        slow = slow.Next
        if fast == slow {
            return true  // If fast and slow pointers meet, there is a cycle
        }
    }
    return false
}

JavaScript:

var hasCycle = function(head) {
    let fast = head;
    let slow = head;
    // A null list or a single node list will definitely not have a cycle
    while(fast != null && fast.next != null){
        fast = fast.next.next; // Fast pointer, moving two steps at a time
        slow = slow.next; // Slow pointer, moving one step at a time
        if(fast === slow) return true; // If fast and slow pointers meet, there is a cycle
    }
    return false; // Reached the end of the list normally, indicating no cycle
};

TypeScript:

function hasCycle(head: ListNode | null): boolean {
    let slowNode: ListNode | null = head,
        fastNode: ListNode | null = head;
    while (fastNode !== null && fastNode.next !== null) {
        slowNode = slowNode!.next;
        fastNode = fastNode.next.next;
        if (slowNode === fastNode) return true;
    }
    return false;
};