54. Spiral Matrix

LeetCode Problem Link (opens new window)

Given an m x n matrix, return all elements of the matrix in spiral order clockwise.

Example 1:

Input:

[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

Output: [1,2,3,6,9,8,7,4,5]

Approach

The approach to solve this problem is derived from 59. Spiral Matrix II (opens new window). It is recommended to review 59. Spiral Matrix II before tackling this problem.

The same principle applies: we're simulating the clockwise spiral traversal of the rectangle. Therefore, the core is to maintain the loop invariant, adhering to the principle of left closed and right open intervals.

Simulating the process of drawing the matrix in a clockwise spiral:

• Fill the upper row from left to right
• Fill the right column from top to bottom
• Fill the lower row from right to left
• Fill the left column from bottom to top

Draw one circle at a time, as shown below:

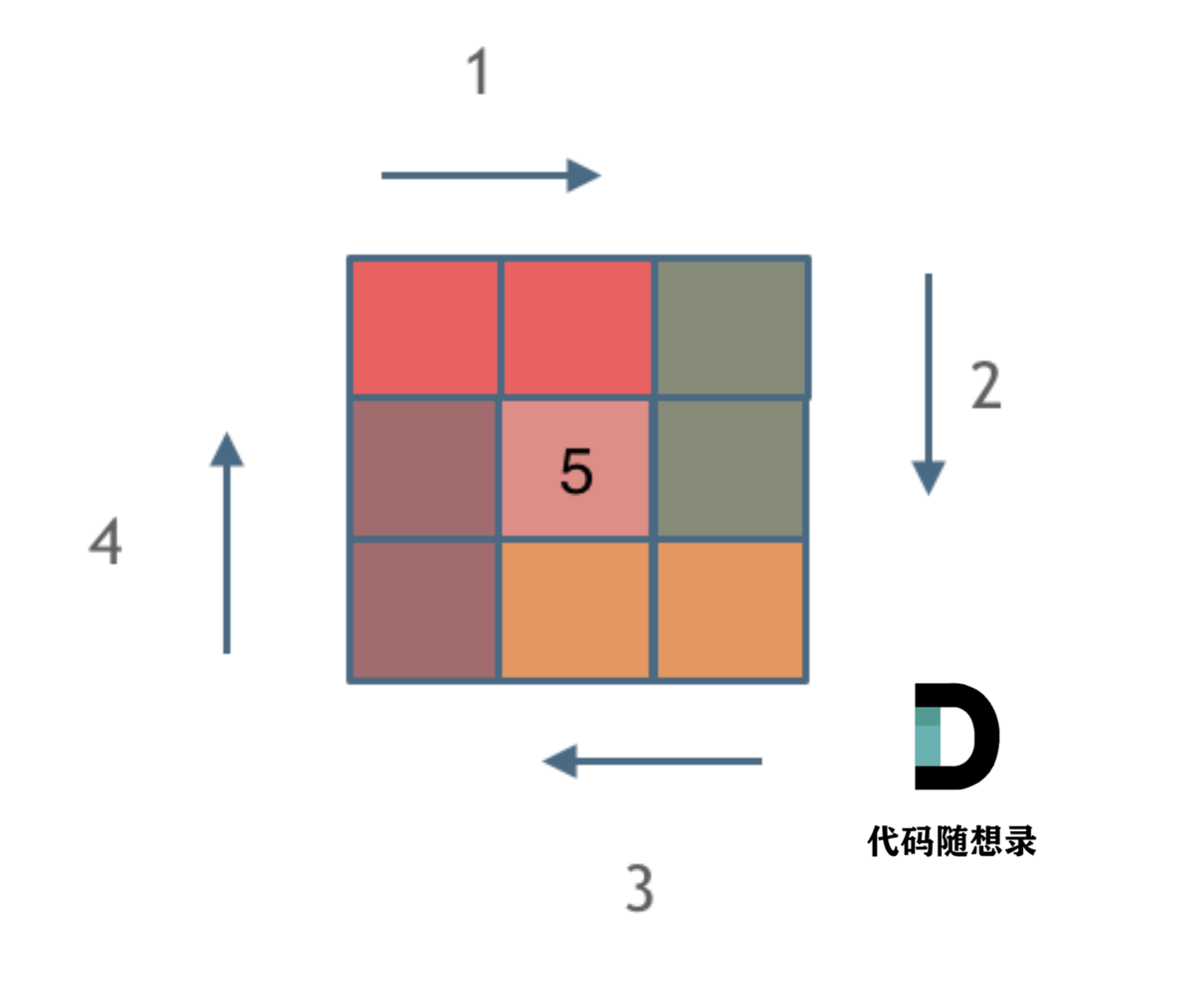
Each color represents an edge, showcasing the handling rules at each corner, where the corner is ceded to the new edge to continue drawing.

The difference from 59. Spiral Matrix II is that the previous problem's matrix is a square and only has the side length n as a boundary condition, whereas in this problem, we need to consider the two boundary conditions of a rectangle's length and width (m rows and n columns). Naturally, m can be equal to n, making the previous problem a special case of this problem when m == n.

Starting with the most general case, we analyze, accompanied by differences introduced by m and n:

• Calculation of loops: The loop calculation differs slightly from the algorithm in 59. Spiral Matrix II because of the existence of two dimensions: rows and columns. The loop is determined only as min(rows, columns), for instance, if rows = 5 and columns = 7, then loop = 5 / 7 = 2.
• Calculation and filling of the middle:
  1. Similarly, the mid calculation in this problem also differs due to the above differences.
  2. • If min(rows, columns) is even, there's no need to consider additional filling of the central position.
     • If min(rows, columns) is odd, then the central part of the matrix is not merely [mid][mid], but there will be a special middle row or middle column left over. Whether it's the middle row or middle column depends on the size of rows and columns. If rows > columns, it's the middle column; otherwise, it's the middle row.

Below is the C++ code, detailed with comments explaining the purpose of each step. Notice that more conditions are checked within the while loop, and the strategy used adheres uniformly to the left closed and right open principle.

Complete C++ code:

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0)
            return {};
        int rows = matrix.size(), columns = matrix[0].size();
        int total = rows * columns;
        vector<int> res(total); // Use vector to define a 1D array to store the result
        int startx = 0, starty = 0; // Define the starting position for each loop
        int loop = min(rows, columns) / 2; 
        // The loop calculation is different from the algorithm in 59. Spiral Matrix II, because there are dimensions of rows and columns; one can figure out that the loop is determined by min(rows, columns). For example, if rows = 5, columns = 7, then loop = 5 / 7 = 2
        int mid = min(rows, columns) / 2; 
        // 1. Similarly, the mid calculation in this problem also differs due to the above differences.
        // 2. 
        //    If min(rows, columns) is even, there's no need to address additional matrix center position values separately.
        //    If min(rows, columns) is odd, the central part of the matrix is not merely [mid][mid], but there will be a special middle row or middle column left. Whether it is a middle row or column depends on the size of rows and columns. If rows > columns, it's a middle column; otherwise, it's a middle row.
        // This aspect can be difficult to understand, and readers are advised to draw their diagrams for better comprehension.
        int count = 0;// Used to populate every cell in the matrix
        int offset = 1;// In each loop, need to control the length of each edge traversal
        int i,j;
        while (loop --) {
            i = startx;
            j = starty;

            // The four following loops simulate one circle
            // Simulate filling the top row from left to right (left closed, right open)
            for (j = starty; j < starty + columns - offset; j++) {
                res[count++] = matrix[startx][j];
            }
            // Simulate filling the right column from top to bottom (left closed, right open)
            for (i = startx; i < startx + rows - offset; i++) {
                res[count++] = matrix[i][j];
            }
            // Simulate filling the bottom row from right to left (left closed, right open)
            for (; j > starty; j--) {
                res[count++] = matrix[i][j];
            }
            // Simulate filling the left column from bottom to top (left closed, right open)
            for (; i > startx; i--) {
                res[count++] = matrix[i][starty];
            }

            // Starting from the second circle, the starting positions each increment. For example, the first circle starts at (0, 0), the second starts at (1, 1)
            startx++;
            starty++;

            // Offset controls the traversal length of each edge in each circle
            offset += 2;
        }

        // If min(rows, columns) is odd, need to handle the central matrix position separately
        if (min(rows, columns) % 2) {
            if(rows > columns){
                for (int i = mid; i < mid + rows - columns + 1; ++i) {
                    res[count++] = matrix[i][mid];
                }

            } else {
                for (int i = mid; i < mid + columns - rows + 1; ++i) {
                    res[count++] = matrix[mid][i];
                }
            }
        }
        return res;
    }
};

Similar Problems

• 59. Spiral Matrix II (opens new window)
• JianZhi Offer 29. Print Matrix Clockwise (opens new window)

Other Language Versions

Java

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        // Store the numbers in the array
        List<Integer> ans = new ArrayList<>();
        // Number of columns
        int columns = matrix[0].length;
        // Number of rows
        int rows = matrix.length;
        // Starting point for traversal
        int start = 0;
        // Number of loops, the smallest in value between the number of rows and columns divided by two
        int loop = Math.min(rows,columns) / 2;
        // The column (or row) index of the intermediate column (row) not traversed
        int mid = loop;
        // Termination condition
        int offSet = 1;
        int i, j;
        while(loop-- > 0) {
            // Initialize starting point
            i = j = start;
            
            // Left to right
            for(; j < columns - offSet; j++)
                ans.add(matrix[i][j]);

            // Top to bottom
            for(; i < rows - offSet; i++)
                ans.add(matrix[i][j]);

            // Right to left
            for(; j > start; j--)
                ans.add(matrix[i][j]);
            
            // Bottom to top
            for(; i > start; i--)
                ans.add(matrix[i][j]);

            // Change start position each loop
            start++;
            // Adjust termination condition
            offSet++;
        }

        // If the smallest of the rows and columns is odd, a middle row or middle column will remain untraversed
        if(Math.min(rows,columns) % 2 != 0) {
            // If rows are greater than columns, there will be an intermediate column
            if(rows > columns) {
                // The next index of the last row of the intermediate column is mid + rows - columns + 1
                for(int k = mid; k < mid + rows - columns + 1; k++) {
                    ans.add(matrix[k][mid]);
                }
            } else {// If columns are greater than or equal to rows, an intermediate row will appear
                // The next index of the last column for the intermediate row is mid + columns - rows + 1
                for(int k = mid; k < mid + columns - rows + 1; k++) {
                    ans.add(matrix[mid][k]);
                }
            }
        }
        return ans;
    }
}

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res = new ArrayList<>(); // Store results
        if (matrix.length == 0 || matrix[0].length == 0)
            return res;
        int rows = matrix.length, columns = matrix[0].length;
        int startx = 0, starty = 0;  // Define the starting position for each loop
        int loop = 0; // Number of loops
        int offset = 1; // Control the length of traversal of each edge in each loop
        while (loop < Math.min(rows, columns) / 2) {
            int i = startx;
            int j = starty;
            // Simulate filling the top row from left to right (left closed, right open)
            for (; j < columns - offset; j++) {
                res.add(matrix[i][j]);
            }
            // Simulate filling the right column from top to bottom (left closed, right open)
            for (; i < rows - offset; i++) {
                res.add(matrix[i][j]);
            }
            // Simulate filling the bottom row from right to left (left closed, right open)
            for (; j > starty; j--) {
                res.add(matrix[i][j]);
            }
            // Simulate filling the left column from bottom to top (left closed, right open)
            for (; i > startx; i--) {
                res.add(matrix[i][j]);
            }

            // Increment the start position and number of loops, adjust traversal length
            startx++;
            starty++;
            offset++;
            loop++;
        }

        // If the minimum of rows or columns is odd, an untraversed part is guaranteed
        // This can be understood better by drawing a diagram yourself
        if (Math.min(rows, columns) % 2 == 1) {
            // When rows are greater than columns, an untraversed column part remains
            // Traverse it as starting position is at (startx, starty), the next position to traverse
            // Traversal count is rows - columns + 1
            if (rows > columns) {
                for (int i = 0; i < rows - columns + 1; i++) {
                    res.add(matrix[startx++][starty]);
                }
            } else {
                // This case follows similar logic to traverse the untraversed row part
                for (int i = 0; i < columns - rows + 1; i++) {
                    res.add(matrix[startx][starty++]);
                }
            }
        }

        return res;
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    let m = matrix.length
    let n = matrix[0].length

    let startX = startY = 0
    let i = 0
    let arr = new Array(m*n).fill(0)
    let offset = 1
    let loop = mid = Math.floor(Math.min(m,n) / 2)
    while (loop--) {
        let row = startX
        let col = startY
        // -->
        for (; col < n + startY - offset; col++) {
            arr[i++] = matrix[row][col]
        }
        // down
        for (; row < m + startX - offset; row++) {
            arr[i++] = matrix[row][col]
        }
        // <--
        for (; col > startY; col--) {
            arr[i++] = matrix[row][col]
        }
        for (; row > startX; row--) {
            arr[i++] = matrix[row][col]
        }
        startX++
        startY++
        offset += 2
    }
    if (Math.min(m, n) % 2 === 1) {
        if (n > m) {
            for (let j = mid; j < mid + n - m + 1; j++) {
                arr[i++] = matrix[mid][j]
            }
        } else {
            for (let j = mid; j < mid + m - n + 1; j++) {
                arr[i++] = matrix[j][mid]
            }
        }
    }
    return arr
};

Python

class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        if len(matrix) == 0 or len(matrix[0]) == 0 : # Check if List is empty
            return []
        row, col = len(matrix), len(matrix[0]) # Number of rows, columns
        loop = min(row, col) // 2 # Number of loops
        stx, sty = 0, 0 # Starting x, y coordinates
        i, j =0, 0
        count = 0  # Counter
        offset = 1  # Number of cells decreased each loop
        result = [0] * (row * col)
        while loop>0 :# Left closed, right open
            i, j = stx, sty
            while j < col - offset :   # Left to right
                result[count] = matrix[i][j]
                count += 1
                j += 1  
            while i < row - offset : # Top to bottom
                result[count] = matrix[i][j]
                count += 1
                i += 1
            while j>sty :  # Right to left
                result[count] = matrix[i][j]
                count += 1
                j -= 1
            while i>stx :  # Bottom to top
                result[count] = matrix[i][j]
                count += 1
                i -= 1
            stx += 1
            sty += 1
            offset += 1
            loop -= 1
        if min(row, col) % 2 == 1 :  # Check if additional line filling is needed
            i = stx
            if row < col :
                while i < stx + col - row + 1 :
                    result[count] = matrix[stx][i]
                    count += 1
                    i += 1
            else :
                while i < stx + row - col + 1 :
                    result[count] = matrix[i][stx]
                    count += 1
                    i += 1
        return result

Version 2: Define four boundaries

class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
            """
        if not matrix:
            return []

        rows = len(matrix)
        cols = len(matrix[0])
        top, bottom, left, right = 0, rows - 1, 0, cols - 1
        print_list = []

        while top <= bottom and left <= right:
            # Left to right
            for i in range(left, right + 1):
                print_list.append(matrix[top][i])
            top += 1

            # Top to bottom
            for i in range(top, bottom + 1):
                print_list.append(matrix[i][right])
            right -= 1

            # Right to left
            if top <= bottom:
                for i in range(right, left - 1, -1):
                    print_list.append(matrix[bottom][i])
                bottom -= 1

            # Bottom to top
            if left <= right:
                for i in range(bottom, top - 1, -1):
                    print_list.append(matrix[i][left])
                left += 1

        return print_list

Go

func spiralOrder(matrix [][]int) []int {
    rows := len(matrix)
    if rows == 0 {
        return []int{}
    }
    columns := len(matrix[0])
    if columns == 0 {
        return []int{}
    }
    res := make([]int, rows * columns)
    startx, starty := 0, 0 // Define the starting position for each loop
    loop := min(rows, columns) / 2
    mid := min(rows, columns) / 2
    count := 0 // Used to populate every cell in the matrix
    offset := 1 // In each loop, need to control the length of traversal of each edge
    for loop > 0 {
        i, j := startx, starty
		
        // Simulate filling the top row from left to right (left closed, right open)
        for ; j < starty + columns - offset; j++ {
            res[count] = matrix[startx][j]
            count++
        }
        // Simulate filling the right column from top to bottom (left closed, right open)
        for ; i < startx + rows - offset; i++ {
            res[count] = matrix[i][j]
            count++
        }
        // Simulate filling the bottom row from right to left (left closed, right open)
        for ; j > starty; j-- {
            res[count] = matrix[i][j]
            count++
        }
        // Simulate filling the left column from bottom to top (left closed, right open)
        for ; i > startx; i-- {
            res[count] = matrix[i][starty]
            count++
        }
        
        // Starting from the second circle, the starting positions each increment. For example, the first circle starts at (0, 0), the second starts at (1, 1)
        startx++
        starty++
        
        // Offset controls the traversal length of each edge in each circle
        offset += 2
        loop--
    }
    
    // If min(rows, columns) is odd, need to handle the central matrix position separately
    if min(rows, columns) % 2 == 1 {
        if rows > columns {
            for i := mid; i < mid + rows - columns + 1; i++ {
                res[count] = matrix[i][mid]
                count++
            }
        } else {
            for i := mid; i < mid + columns - rows + 1; i++ {
                res[count] = matrix[mid][i]
                count++
            }
        }
    }
    return res
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}