1. Two Sum

LeetCode Problem Link (opens new window)

Given an array of integers nums and an integer target, return the indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

Example:

Given nums = [2, 7, 11, 15], target = 9

Because nums[0] + nums[1] = 2 + 7 = 9

Return [0, 1]

Approach

Clearly, a brute force solution is to use two nested for loops to find the answer, with a time complexity of O(n^2).

Before attempting this problem, it is recommended to solve the following two problems:

• 0242.Valid Anagram (opens new window)
• 0349.Intersection of Two Arrays (opens new window)

The problem 0242.Valid Anagram (opens new window) is solved using an array as a hash table to address the hash concern, while the problem 0349.Intersection of Two Arrays (opens new window) utilizes a set as a hash table to solve the hash concern.

First, let me emphasize when to use the hashing method. When you need to check if an element has appeared before, or if it is within a set, the first thought should be the hashing method.

In this problem, I need a collection to store the elements we've traversed so far, and as we iterate through the array, we need to ask whether an element has been traversed, i.e., whether it is in this collection.

So, we should think about using the hashing method.

Since in this problem, we not only need to know if an element has been traversed, but also need to know the index corresponding to this element, we need to store a key-value structure: key to store the element, and value to store the index. Therefore, using a map is a perfect fit.

Let's see the limitations of using an array and set as a hashing method.

• The size of an array is limited, and if there are few elements but the hash value is large, it might cause a waste of memory space.
• A set is a collection that can only hold one key, but the problem Two Sum requires not only checking if y exists but also recording the index of y because we need to return the indices of x and y. Thus, a set is not suitable.

At this point, we should choose another data structure: a map. A map is a key-value storage structure where the key can be used to store the value, and the value can store the index.

In C++, there are three types of maps:

Mapping	Underlying Implementation	Ordered	Duplicate Keys	Modifiable Keys	Lookup Complexity	Insert/Delete Complexity
std::map	Red-Black Tree	Key ordered	Keys not repeatable	Keys unmodifiable	O(log n)	O(log n)
std::multimap	Red-Black Tree	Key ordered	Keys repeatable	Keys unmodifiable	O(log n)	O(log n)
std::unordered_map	Hash Table	Key unordered	Keys not repeatable	Keys unmodifiable	O(1)	O(1)

std::unordered_map has an underlying implementation of a hash table, std::map and std::multimap are implemented as red-black trees.

Similarly, the keys in std::map and std::multimap are ordered (this is often a topic of interviews to test the understanding of the container's underlying implementation in languages). For more theoretical knowledge about Hash Tables, please refer to Hash Table Basics (opens new window).

In this problem, we don't need ordered keys, so using std::unordered_map is more efficient! Users of other languages should understand the data structures in their languages just as well.

Let's be clear on two points:

• What is the map used for?
• What do the key and value in the map represent?

The purpose of the map is to store the elements we have visited because as we traverse the array, we need to record which elements we encountered along with their indices. This allows us to find a match for the current element (i.e., sum equals target).

Next, what do the key and value in the map represent?

For this problem, we need to provide an element and check if it has appeared before. If it has, we return the indices.

So, if we're checking if an element has appeared, this element should be the key. Therefore, elements in the array are the keys, and connected with the keys are the values, which are used to store indices.

So the storage structure in the map is {key: array element, value: index of the array element}.

As we traverse the array, we just need to query the map for a matching value of the current element. If a match is found, we've got our solution, and if not, we add the current traversed element to the map, which stores the elements we've seen.

The process is as follows:

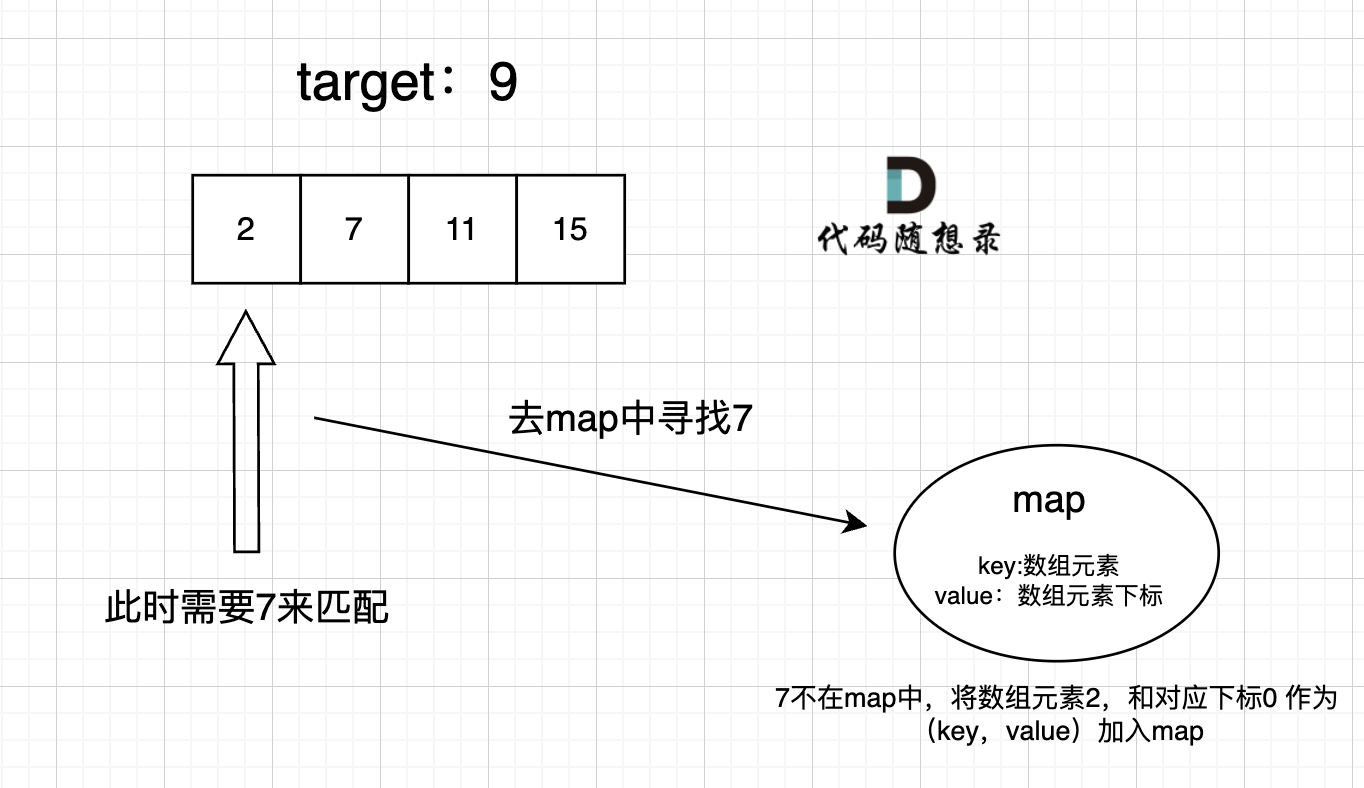
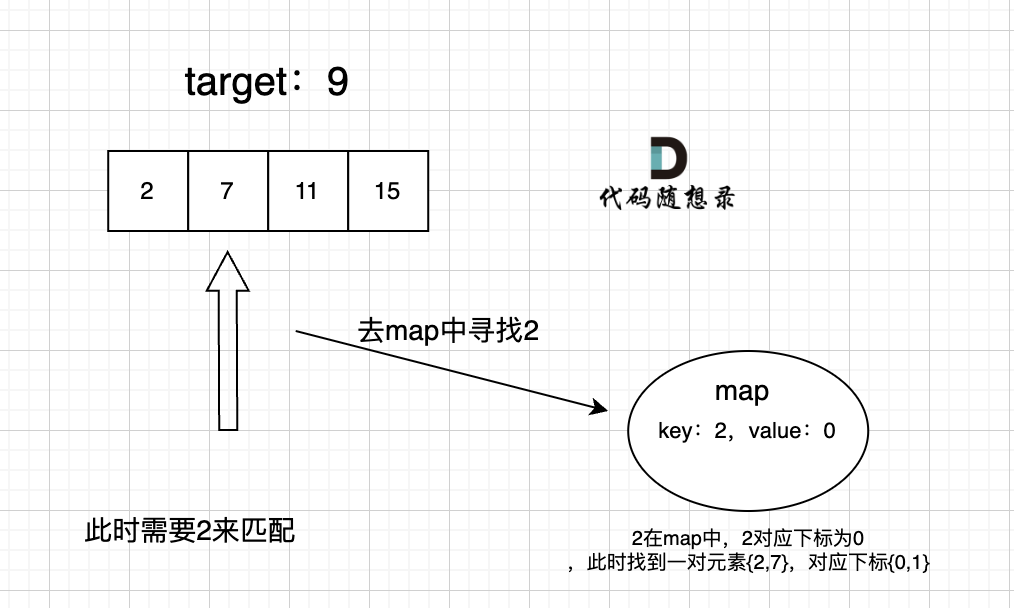
C++ code:

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        std::unordered_map <int,int> map;
        for(int i = 0; i < nums.size(); i++) {
            // Traverse current element and lookup in map for a matching key
            auto iter = map.find(target - nums[i]); 
            if(iter != map.end()) {
                return {iter->second, i};
            }
            // If no match is found, add the visited element and index to map
            map.insert(pair<int, int>(nums[i], i)); 
        }
        return {};
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

Summary

There are actually four key points in this question:

• Why did we think of using a hash table
• Why is a map used as the hash table
• What is stored in the map in this question
• What is the key and value in the map stored as

To truly understand this question, make sure you have a clear understanding of these four points.

While many have passed this problem, they haven't thought through what the map is used for, resulting in only a partial understanding of the code.

Other Language Versions

Java:

//Using Hash Table
public int[] twoSum(int[] nums, int target) {
    int[] res = new int[2];
    if(nums == null || nums.length == 0){
        return res;
    }
    Map<Integer, Integer> map = new HashMap<>();
    for(int i = 0; i < nums.length; i++){
        int temp = target - nums[i];   // Traverse current element and lookup in map for a matching key
        if(map.containsKey(temp)){
            res[1] = i;
            res[0] = map.get(temp);
            break;
        }
        map.put(nums[i], i);    // If no match is found, add the visited element and index to map
    }
    return res;
}

//Using Hash Table method 2
public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> indexMap = new HashMap<>();
    
    for(int i = 0; i < nums.length; i++){
        int balance = target - nums[i];  // Record the remaining part for the current target value
        if(indexMap.containsKey(balance)){  // Check if the map contains a satisfying value
            return new int []{i, indexMap.get(balance)}; // If so, return the indices of the values
        } else{
            indexMap.put(nums[i], i); // If not, add the visited element and index to map
        }
    }
    return null;
}

//Using Two Pointers
public int[] twoSum(int[] nums, int target) {
    int m=0,n=0,k,board=0;
    int[] res=new int[2];
    int[] tmp1=new int[nums.length];
    // Backup of the original indices in the nums array
    System.arraycopy(nums,0,tmp1,0,nums.length);
    // Sort the nums
    Arrays.sort(nums);
    // Two pointers
    for(int i=0,j=nums.length-1;i<j;){
        if(nums[i]+nums[j]<target)
            i++;
        else if(nums[i]+nums[j]>target)
            j--;
        else if(nums[i]+nums[j]==target){
            m=i;
            n=j;
            break;
        }
    }
    // Find the index of nums[m] in the tmp1 array
    for(k=0;k<nums.length;k++){
        if(tmp1[k]==nums[m]){
            res[0]=k;
            break;
        }
    }
    // Find the index of nums[n] in the tmp1 array
    for(int i=0;i<nums.length;i++){
        if(tmp1[i]==nums[n]&&i!=k)
            res[1]=i;
    }
    return res;
}

Python:

(Version 1) Using dictionary

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        records = dict()

        for index, value in enumerate(nums):  
            if target - value in records:   # Traverse current element and lookup in map for a matching key
                return [records[target- value], index]
            records[value] = index    # If no match is found, add the visited element and index to map
        return []

(Version 2) Using set

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # Create a set to store the numbers we've seen
        seen = set()             
        for i, num in enumerate(nums):
            complement = target - num
            if complement in seen:
                return [nums.index(complement), i]
            seen.add(num)

(Version 3) Using Two Pointers

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # Sort the input list
        nums_sorted = sorted(nums)
        
        # Use two pointers
        left = 0
        right = len(nums_sorted) - 1
        while left < right:
            current_sum = nums_sorted[left] + nums_sorted[right]
            if current_sum == target:
                # If the sum equals the target, return the indices of the two numbers
                left_index = nums.index(nums_sorted[left])
                right_index = nums.index(nums_sorted[right])
                if left_index == right_index:
                    right_index = nums[left_index+1:].index(nums_sorted[right]) + left_index + 1
                return [left_index, right_index]
            elif current_sum < target:
                # If the sum is less than target, move the left pointer right
                left += 1
            else:
                # If the sum is greater than target, move the right pointer left
                right -= 1

(Version 4) Brute-force

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            for j in range(i+1, len(nums)):
                if nums[i] + nums[j] == target:
                    return [i,j]

Go:

// Brute-force solution
func twoSum(nums []int, target int) []int {
    for k1, _ := range nums {
        for k2 := k1 + 1; k2 < len(nums); k2++ {
            if target == nums[k1] + nums[k2] {
                return []int{k1, k2}
            }
        }
    }
    return []int{}
}

func twoSum(nums []int, target int) []int {
    m := make(map[int]int)
    for i, num := range nums {
        complement := target - num
        if index, found := m[complement]; found {
            return []int{index, i}
        }
        m[num] = i
    }
    return nil  // Return an empty array with nil instead of an empty slice
}

Rust:

use std::collections::HashMap;

impl Solution {
    pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
        let mut map = HashMap::with_capacity(nums.len());

        for i in 0..nums.len() {
            if let Some(k) = map.get(&(target - nums[i])) {
                if *k != i {
                    return vec![*k as i32,  i as i32];
                }
            }
            map.insert(nums[i], i);
        }
        panic!("not found")
    }
}

use std::collections::HashMap;
 
impl Solution {
    pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
        let mut hm: HashMap<i32, i32> = HashMap::new();
        for i in 0..nums.len() {
            let j = target - nums[i];
            if hm.contains_key(&j) {
                return vec![*hm.get(&j).unwrap(), i as i32]
            } else {
                hm.insert(nums[i], i as i32);
            }
        }
        vec![-1, -1]
    }
}

JavaScript:

var twoSum = function (nums, target) {
  let hash = {};
  for (let i = 0; i < nums.length; i++) {  // Traverse current element and lookup in map for a matching key
    if (hash[target - nums[i]] !== undefined) {
      return [i, hash[target - nums[i]]];
    }
    hash[nums[i]] = i;   // If no match is found, add the visited element and index to map
  }
  return [];
};

TypeScript：

function twoSum(nums: number[], target: number): number[] {
    let helperMap: Map<number, number> = new Map();
    let index: number | undefined;
    let resArr: number[] = [];
    for (let i = 0, length = nums.length; i < length; i++) {
        index = helperMap.get(target - nums[i]);
        if (index !== undefined) {
            resArr = [i, index];
            break;
        }
        helperMap.set(nums[i], i);
    }
    return resArr;
};

PhP:

function twoSum(array $nums, int $target): array
{
    $map = [];
    foreach($nums as $i => $num) {
        if (isset($map[$target - $num])) {
            return [
                $i,
                $map[$target - $num]
            ];
        } else {
            $map[$num] = $i;
        }
    }
    return [];
}

Swift：

func twoSum(_ nums: [Int], _ target: Int) -> [Int] {
    // Value: Index
    var map = [Int: Int]()
    for (i, e) in nums.enumerated() {
        if let v = map[target - e] {
            return [v, i]
        } else {
            map[e] = i
        }
    }
    return []
}

Scala:

object Solution {
  // Import necessary package
  import scala.collection.mutable
  def twoSum(nums: Array[Int], target: Int): Array[Int] = {
    // Key stores value, value stores index
    val map = new mutable.HashMap[Int, Int]()
    for (i <- nums.indices) {
      val tmp = target - nums(i) // Calculate complement
      // If the map contains the complement, a solution is found
      if (map.contains(tmp)) {
        return Array(map.get(tmp).get, i)
      }
      // If not, add the current value and its index to the map
      map.put(nums(i), i)
    }
    // If not found, directly return an empty array, the 'return' keyword can be omitted
    new Array[Int](2)
  }
}

C#:

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        Dictionary<int ,int> dic= new Dictionary<int,int>();
        for(int i=0;i<nums.Length;i++){
            int imp= target-nums[i];
            if(dic.ContainsKey(imp)&&dic[imp]!=i){
               return new int[]{i, dic[imp]};
            }
            if(!dic.ContainsKey(nums[i])){
                dic.Add(nums[i],i);
            }
        }
        return new int[]{0, 0};
    }
}

Dart:

import 'dart:collection';

List<int> twoSum(List<int> nums, int target) {
  HashMap<int, int> hashMap = HashMap();
  for (int i = 0; i < nums.length; i++) {
    int rest = target - nums[i];
    if (hashMap.containsKey(rest)) {
      return [hashMap[rest]!, i];
    }
    hashMap.addEntries({nums[i]: i}.entries);
  }
  return [];
}

C:

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

// leetcode supports ut_hash library

 typedef struct {
     int key;
     int value;
     UT_hash_handle hh; // make this structure hashable
 } map;

map* hashMap = NULL;

 void hashMapAdd(int key, int value){
     map* s;
     // key already in the hash?
     HASH_FIND_INT(hashMap, &key, s);
     if(s == NULL){
         s = (map*)malloc(sizeof(map));
         s -> key = key;
         HASH_ADD_INT(hashMap, key, s);
     }
     s -> value = value;
 }

map* hashMapFind(int key){
     map* s;
     // *s: output pointer
     HASH_FIND_INT(hashMap, &key, s);   
     return s;
 }

 void hashMapCleanup(){
     map* cur, *tmp;
     HASH_ITER(hh, hashMap, cur, tmp){
         HASH_DEL(hashMap, cur);
         free(cur);
     }
 }

 void hashPrint(){
     map* s;
     for(s = hashMap; s != NULL; s=(map*)(s -> hh.next)){
         printf("key %d, value %d\n", s -> key, s -> value);
     }
 }

 
int* twoSum(int* nums, int numsSize, int target, int* returnSize){
    int i, *ans;
    // hash find result
    map* hashMapRes; 
    hashMap = NULL;
    ans = malloc(sizeof(int) * 2);

    for(i = 0; i < numsSize; i++){
        // key represents the value of nums[i], value represents the index
        hashMapAdd(nums[i], i);
    }

    hashPrint();

    for(i = 0; i < numsSize; i++){
        hashMapRes = hashMapFind(target - nums[i]);
        if(hashMapRes && hashMapRes -> value != i){
            ans[0] = i;
            ans[1] = hashMapRes -> value ;
            *returnSize = 2;
            return ans;
        }
    }
    
    hashMapCleanup();
    return NULL;
}