# Problem 15. 3Sum
LeetCode Problem Link (opens new window)
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
The set of triplets should be:
[
[-1, 0, 1],
[-1, -1, 2]
]
2
3
4
# Solution
# Hashing Method
A straightforward hashing solution involves a double loop to find two values, and then using a hash map to check if the third value, 0 - (a + b), exists in the array. This solution is valid but has the tricky requirement of not including duplicate triplets in the result.
Removing duplicate triplets from the result vector can be quite time-consuming and often leads to time limit exceeded errors. It's a major reason why this problem has a relatively low acceptance rate. Carefully handling the details of duplicate removal can be challenging in a technical interview.
The time complexity can be reduced to O(n^2), but due to limited pruning ability, it still might perform suboptimal.
You are encouraged to try implementing this with a hash map to grasp its difficulty.
Hashing Method in C++:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > 0)
break;
if (i > 0 && nums[i] == nums[i - 1])
continue;
unordered_set<int> set;
for (int k = i + 1; k < nums.size(); k++) {
if (k > i + 2 && nums[k] == nums[k - 1] && nums[k - 1] == nums[k - 2])
continue;
int target = 0 - (nums[i] + nums[k]);
if (set.find(target) != set.end()) {
result.push_back({nums[i], target, nums[k]});
set.erase(target);
}
else {
set.insert(nums[k]);
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
- Time Complexity: O(n^2)
- Space Complexity: O(n), due to the extra set space.
# Two-Pointer Method
The hashing method is not the most suitable for this problem due to its intricacies in removing duplicates efficiently. A more effective approach is the two-pointer technique, which offers better efficiency than hashing.
Animated Explanation:
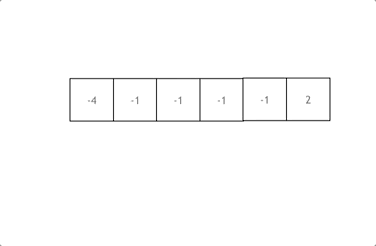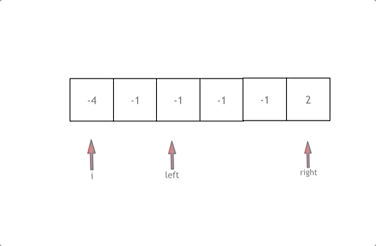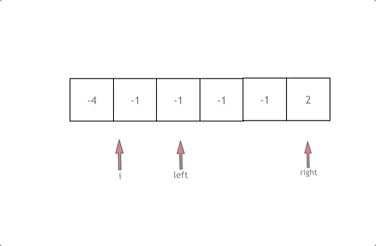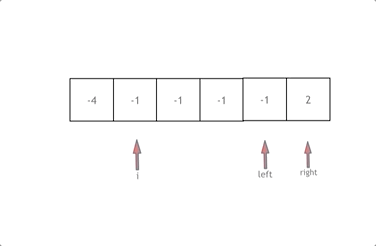
Consider the array nums, first sort it. Initiate a loop where i starts at 0, left is i + 1, and right is the array's end.
Our goal is to find a, b, and c such that a + b + c = 0. Here, a = nums[i], b = nums[left], c = nums[right].
Move left and right pointers based on their sum; if the sum is more than zero, decrement right for a smaller sum. If less, increment left. Continue until left meets right.
The time complexity is O(n^2).
C++ Code:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > 0) {
return result;
}
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.size() - 1;
while (right > left) {
if (nums[i] + nums[left] + nums[right] > 0) right--;
else if (nums[i] + nums[left] + nums[right] < 0) left++;
else {
result.push_back(vector<int>{nums[i], nums[left], nums[right]});
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
right--;
left++;
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
- Time Complexity: O(n^2)
- Space Complexity: O(1)
# Considerations for Duplicates
# Duplicates of element a
For handling duplicates of a in the triplets a, b, c (corresponding to nums[i], nums[left], nums[right]), if a is repeated, skip it. Compare nums[i] with nums[i-1] rather than nums[i+1] to avoid missing cases like {-1, -1, 2}.
# Duplicates of elements b and c
In practice, there isn't a need to remove duplicates of left and right during the checks as it won't improve efficiency. The existing logic already covers these without redundancy in evaluations.
# Discussion Question
Given the success of the two-pointer method for three-sum, can it be applied to the 1. Two Sum (opens new window) problem too? If not, how could the problem's terms be adjusted to facilitate the use of two-pointers?
For two-sum, the two-pointer method isn't appropriate because it requires returning index positions, and sorting alters indices. If the problem instead required the return of values, the two-pointer approach might be applicable.
# Additional Language Solutions
# Java:
(Version 1) Two-Pointer
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
return result;
}
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (right > left) {
int sum = nums[i] + nums[left] + nums[right];
if (sum > 0) {
right--;
} else if (sum < 0) {
left++;
} else {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
right--;
left++;
}
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
(Version 2) Using Hash Set
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
return result;
}
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
HashSet<Integer> set = new HashSet<>();
for (int j = i + 1; j < nums.length; j++) {
if (j > i + 2 && nums[j] == nums[j - 1] && nums[j - 1] == nums[j - 2]) {
continue;
}
int c = -nums[i] - nums[j];
if (set.contains(c)) {
result.add(Arrays.asList(nums[i], nums[j], c));
set.remove(c);
} else {
set.add(nums[j]);
}
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Python:
(Version 1) Two-Pointer
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
for i in range(len(nums)):
if nums[i] > 0:
return result
if i > 0 and nums[i] == nums[i - 1]:
continue
left = i + 1
right = len(nums) - 1
while right > left:
sum_ = nums[i] + nums[left] + nums[right]
if sum_ < 0:
left += 1
elif sum_ > 0:
right -= 1
else:
result.append([nums[i], nums[left], nums[right]])
while right > left and nums[right] == nums[right - 1]:
right -= 1
while right > left and nums[left] == nums[left + 1]:
left += 1
right -= 1
left += 1
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
(Version 2) Using Dictionary
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
for i in range(len(nums)):
if nums[i] > 0:
break
if i > 0 and nums[i] == nums[i - 1]:
continue
d = {}
for j in range(i + 1, len(nums)):
if j > i + 2 and nums[j] == nums[j-1] == nums[j-2]:
continue
c = 0 - (nums[i] + nums[j])
if c in d:
result.append([nums[i], nums[j], c])
d.pop(c)
else:
d[nums[j]] = j
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Go:
(Version 1) Two-Pointer
func threeSum(nums []int) [][]int {
sort.Ints(nums)
res := [][]int{}
for i := 0; i < len(nums)-2; i++ {
n1 := nums[i]
if n1 > 0 {
break
}
if i > 0 && n1 == nums[i-1] {
continue
}
l, r := i+1, len(nums)-1
for l < r {
n2, n3 := nums[l], nums[r]
if n1+n2+n3 == 0 {
res = append(res, []int{n1, n2, n3})
while l < r && nums[l] == n2 {
l++
}
while l < r && nums[r] == n3 {
r--
}
} else if n1+n2+n3 < 0 {
l++
} else {
r--
}
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
(Version 2) Hashing Method
func threeSum(nums []int) [][]int {
res := make([][]int, 0)
sort.Ints(nums)
for i := 0; i < len(nums); i++ {
if nums[i] > 0 {
break
}
if i > 0 && nums[i] == nums[i-1] {
continue
}
set := make(map[int]struct{})
for j := i + 1; j < len(nums); j++ {
if j > i + 2 && nums[j] == nums[j-1] && nums[j-1] == nums[j-2] {
continue
}
c := -nums[i] - nums[j]
if _, ok := set[c]; ok {
res = append(res, []int{nums[i], nums[j], c})
delete(set, c)
} else {
set[nums[j]] = struct{}{}
}
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# JavaScript:
var threeSum = function(nums) {
const res = [], len = nums.length;
nums.sort((a, b) => a - b);
for (let i = 0; i < len; i++) {
let l = i + 1, r = len - 1, iNum = nums[i];
if (iNum > 0) return res;
if (iNum == nums[i - 1]) continue;
while(l < r) {
let lNum = nums[l], rNum = nums[r], threeSum = iNum + lNum + rNum;
if (threeSum < 0) l++;
else if (threeSum > 0) r--;
else {
res.push([iNum, lNum, rNum]);
while(l < r && nums[l] == nums[l + 1]){
l++;
}
while(l < r && nums[r] == nums[r - 1]) {
r--;
}
l++;
r--;
}
}
}
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Solution two: General nSum implementation (recursive)
/**
* General solution for nSum, supporting 2sum, 3sum, 4sum, etc.
* Time Complexity Analysis:
* 1. When n = 2, the time complexity is O(NlogN) due to sorting.
* 2. When n > 2, the time complexity is O(N^(n-1)), at least quadratic, so sorting time can be omitted. For example, 3sum is O(n^2), 4sum is O(n^3).
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function (nums) {
// Core nSum general solution function
function nSumTarget(nums, n, start, target) {
nums.sort((a, b) => a - b);
let res = [];
if (n === 2) {
res = twoSumTarget(nums, start, target);
} else {
for (let i = start; i < nums.length; i++) {
let subRes = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (let j = 0; j < subRes.length; j++) {
res.push([nums[i], ...subRes[j]]);
}
while (nums[i] === nums[i + 1]) i++;
}
}
return res;
}
function twoSumTarget(nums, start, target) {
let res = [];
let len = nums.length;
let left = start;
let right = len - 1;
while (left < right) {
let sum = nums[left] + nums[right];
if (sum < target) {
while (nums[left] === nums[left + 1]) left++;
left++;
} else if (sum > target) {
while (nums[right] === nums[right - 1]) right--;
right--;
} else {
res.push([nums[left], nums[right]]);
while (nums[left] === nums[left + 1]) left++;
while (nums[right] === nums[right - 1]) right--;
left++;
right--;
}
}
return res;
}
return nSumTarget(nums, 3, 0, 0);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# TypeScript:
function threeSum(nums: number[]): number[][] {
nums.sort((a, b) => a - b);
let length = nums.length;
let left: number = 0,
right: number = length - 1;
let resArr: number[][] = [];
for (let i = 0; i < length; i++) {
if (nums[i] > 0) {
return resArr;
}
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
}
left = i + 1;
right = length - 1;
while (left < right) {
let total: number = nums[i] + nums[left] + nums[right];
if (total === 0) {
resArr.push([nums[i], nums[left], nums[right]]);
left++;
right--;
while (nums[right] === nums[right + 1]) {
right--;
}
while (nums[left] === nums[left - 1]) {
left++;
}
} else if (total < 0) {
left++;
} else {
right--;
}
}
}
return resArr;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Ruby
def is_valid(strs)
symbol_map = {')' => '(', '}' => '{', ']' => '['}
stack = []
strs.size.times {|i|
c = strs[i]
if symbol_map.has_key?(c)
top_e = stack.shift
return false if symbol_map[c] != top_e
else
stack.unshift(c)
end
}
stack.empty?
end
2
3
4
5
6
7
8
9
10
11
12
13
14
# PHP
class Solution {
/**
* @param Integer[] $nums
* @return Integer[][]
*/
function threeSum($nums) {
$res = [];
sort($nums);
for ($i = 0; $i < count($nums); $i++) {
if ($nums[$i] > 0) {
return $res;
}
if ($i > 0 && $nums[$i] == $nums[$i - 1]) {
continue;
}
$left = $i + 1;
$right = count($nums) - 1;
while ($left < $right) {
$sum = $nums[$i] + $nums[$left] + $nums[$right];
if ($sum < 0) {
$left++;
}
else if ($sum > 0) {
$right--;
}
else {
$res[] = [$nums[$i], $nums[$left], $nums[$right]];
while ($left < $right && $nums[$left] == $nums[$left + 1]) $left++;
while ($left < $right && $nums[$right] == $nums[$right - 1]) $right--;
$left++;
$right--;
}
}
}
return $res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Swift
// Two-pointer method
func threeSum(_ nums: [Int]) -> [[Int]] {
var res = [[Int]]()
var sorted = nums
sorted.sort()
for i in 0 ..< sorted.count {
if sorted[i] > 0 {
return res
}
if i > 0 && sorted[i] == sorted[i - 1] {
continue
}
var left = i + 1
var right = sorted.count - 1
while left < right {
let sum = sorted[i] + sorted[left] + sorted[right]
if sum < 0 {
left += 1
} else if sum > 0 {
right -= 1
} else {
res.append([sorted[i], sorted[left], sorted[right]])
while left < right && sorted[left] == sorted[left + 1] {
left += 1
}
while left < right && sorted[right] == sorted[right - 1] {
right -= 1
}
left += 1
right -= 1
}
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Rust
// Hash solution
use std::collections::HashSet;
impl Solution {
pub fn three_sum(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut nums = nums;
nums.sort();
let len = nums.len();
for i in 0..len {
if nums[i] > 0 { break; }
if i > 0 && nums[i] == nums[i - 1] { continue; }
let mut set = HashSet::new();
for j in (i + 1)..len {
if j > i + 2 && nums[j] == nums[j - 1] && nums[j] == nums[j - 2] { continue; }
let c = 0 - (nums[i] + nums[j]);
if set.contains(&c) {
result.push(vec![nums[i], nums[j], c]);
set.remove(&c);
} else { set.insert(nums[j]); }
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// Two-pointer method
use std::cmp::Ordering;
impl Solution {
pub fn three_sum(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut nums = nums;
nums.sort();
let len = nums.len();
for i in 0..len {
if nums[i] > 0 { return result; }
if i > 0 && nums[i] == nums[i - 1] { continue; }
let (mut left, mut right) = (i + 1, len - 1);
while left < right {
match (nums[i] + nums[left] + nums[right]).cmp(&0) {
Ordering::Equal => {
result.push(vec![nums[i], nums[left], nums[right]]);
left += 1;
right -= 1;
while left < right && nums[left] == nums[left - 1] {
left += 1;
}
while left < right && nums[right] == nums[right + 1] {
right -= 1;
}
}
Ordering::Greater => right -= 1,
Ordering::Less => left += 1,
}
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# C
// Qsort helper cmp function
int cmp(const void* ptr1, const void* ptr2) {
return *((int*)ptr1) > *((int*)ptr2);
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {
// Allocate ans array space
int **ans = (int**)malloc(sizeof(int*) * 18000);
int ansTop = 0;
if(numsSize < 3) {
*returnSize = 0;
return ans;
}
qsort(nums, numsSize, sizeof(int), cmp);
int i;
for(i = 0; i < numsSize - 2; i++) {
if(nums[i] > 0)
break;
if(i > 0 && nums[i] == nums[i-1])
continue;
int left = i + 1;
int right = numsSize - 1;
while(right > left) {
int sum = nums[right] + nums[left] + nums[i];
if(sum < 0)
left++;
else if(sum > 0)
right--;
else {
int* arr = (int*)malloc(sizeof(int) * 3);
arr[0] = nums[i];
arr[1] = nums[left];
arr[2] = nums[right];
ans[ansTop++] = arr;
while(right > left && nums[right] == nums[right - 1])
right--;
while(left < right && nums[left] == nums[left + 1])
left++;
left++;
right--;
}
}
}
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int z;
for(z = 0; z < ansTop; z++) {
(*returnColumnSizes)[z] = 3;
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# C#
public class Solution
{
public IList<IList<int>> ThreeSum(int[] nums)
{
var result = new List<IList<int>>();
Array.Sort(nums);
for (int i = 0; i < nums.Length - 2; i++)
{
int n1 = nums[i];
if (n1 > 0)
break;
if (i > 0 && n1 == nums[i - 1])
continue;
int left = i + 1;
int right = nums.Length - 1;
while (left < right)
{
int n2 = nums[left];
int n3 = nums[right];
int sum = n1 + n2 + n3;
if (sum > 0)
{
right--;
}
else if (sum < 0)
{
left++;
}
else
{
result.Add(new List<int> { n1, n2, n3 });
while (left < right && nums[left] == n2)
{
left++;
}
while (left < right && nums[right] == n3)
{
right--;
}
}
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# Scala
object Solution {
import scala.collection.mutable.ListBuffer
import scala.util.control.Breaks.{break, breakable}
def threeSum(nums: Array[Int]): List[List[Int]] = {
val res = ListBuffer[List[Int]]()
val numsTmp = nums.sorted
for (i <- numsTmp.indices) {
if (numsTmp(i) > 0) {
return res.toList
}
breakable {
if (i > 0 && numsTmp(i) == numsTmp(i - 1)) {
break
} else {
var left = i + 1
var right = numsTmp.length - 1
while (left < right) {
val sum = numsTmp(i) + numsTmp(left) + numsTmp(right)
if (sum < 0) left += 1
else if (sum > 0) right -= 1
else {
res += List(numsTmp(i), numsTmp(left), numsTmp(right))
while (left < right && numsTmp(left) == numsTmp(left + 1)) left += 1
while (left < right && numsTmp(right) == numsTmp(right - 1)) right -= 1
left += 1
right -= 1
}
}
}
}
}
res.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
