If the hash values are few, particularly dispersed, and have a very large range, using an array will cause great waste of space!

349. Intersection of Two Arrays

LeetCode Problem Link (opens new window)

Problem Description

Given two arrays, write a function to compute their intersection.

Note: Each element in the result must be unique. The result can be in any order.

Approach

This problem primarily involves learning how to use a hashing data structure: unordered_set. This data structure can solve many similar problems.

Note that the problem specifically states: Each element in the result must be unique, meaning the result should be de-duplicated. Also, you can disregard the order of the output results.

Using a brute force solution has a time complexity of (O(n^2)), so let’s see how we can further optimize it with hashing.

Using an array to mimic a hash table can also be a good choice, like in 0242.Valid Anagram (opens new window).

However, it's important to note that the problems using arrays as hashes usually restrict the size of the values.

In this problem, since there is no restriction on the size of the values, using arrays as hashes is impractical.

Additionally, if the hash values are sparse and the range is large, using arrays would cause excessive space usage.

At this point, another structure, set, should be employed. C++ offers the following structures:

• std::set
• std::multiset
• std::unordered_set

std::set and std::multiset are implemented using red-black trees, while std::unordered_set is implemented through hash tables. Using unordered_set achieves the highest read and write efficiency, does not require data sorting, and avoids duplicate data, making unordered_set an appropriate choice.

The approach is illustrated in the diagram below:

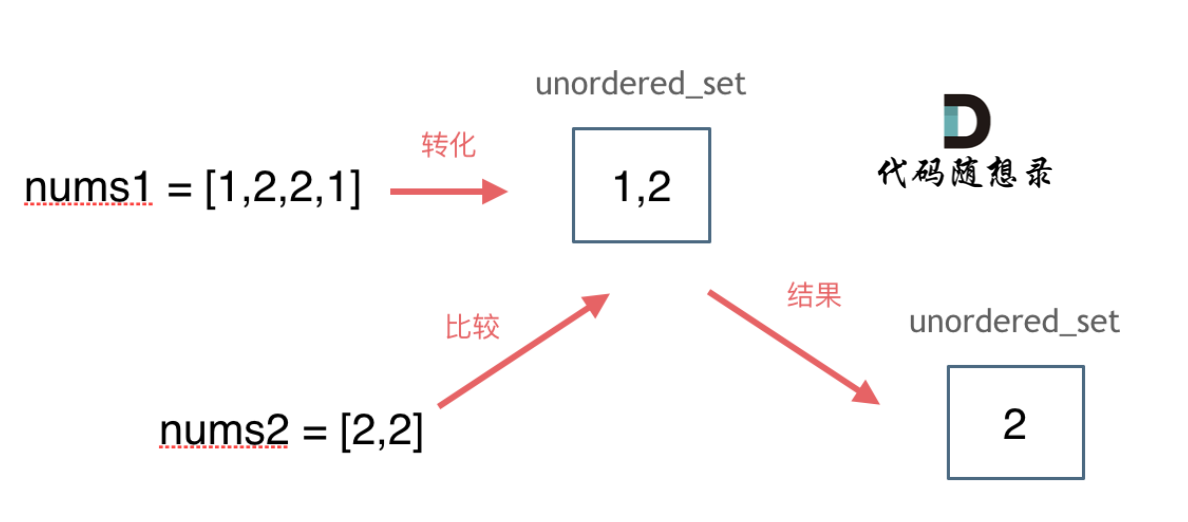
C++ code:

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // Store results; using set to de-duplicate the result set
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for (int num : nums2) {
            // If an element in nums2 is found in nums_set
            if (nums_set.find(num) != nums_set.end()) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

• Time Complexity: (O(n + m)), where (m) is the cost to convert the set into a vector
• Space Complexity: (O(n))

Additional Discussion

Some may wonder, why not always use set for hashing issues?

The direct use of set not only occupies more space than an array but is also slower. Mapping a value onto a key in a set requires hash computation.

Don't underestimate the time cost of this operation. The difference is significant when dealing with a large amount of data.

Postscript

The problem description and backend test data on LeetCode have been updated to include a value range:

• (1 \leq \text{nums1.length}, \text{nums2.length} \leq 1000)
• (0 \leq \text{nums1}[i], \text{nums2}[i] \leq 1000)

Thus, arrays can now be used to implement hash tables since the values are within 1000.

Corresponding C++ code:

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // Store results; using set to de-duplicate results
        int hash[1005] = {0}; // Default value is 0
        for (int num : nums1) { // Record occurrences of elements in nums1 in the hash array
            hash[num] = 1;
        }
        for (int num : nums2) { // If an element appears in nums2, record it in the result
            if (hash[num] == 1) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

• Time Complexity: (O(m + n))
• Space Complexity: (O(n))

Code Versions in Other Languages

Java

Version 1: Using HashSet

// Time Complexity O(n+m+k) Space Complexity O(n+k)
// where n is the length of nums1, m is the length of nums2, and k is the count of intersection elements

import java.util.HashSet;
import java.util.Set;

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
            return new int[0];
        }
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> resSet = new HashSet<>();
        // Traverse through nums1
        for (int i : nums1) {
            set1.add(i);
        }
        // During the traversal of nums2, check if the set contains the element
        for (int i : nums2) {
            if (set1.contains(i)) {
                resSet.add(i);
            }
        }

        // Method 1: Convert result set to an array
        return res.stream().mapToInt(Integer::intValue).toArray();
        
        // Method 2: Allocate a new array to store elements from resSet, and return the array
        int[] arr = new int[resSet.size()];
        int j = 0;
        for(int i : resSet){
            arr[j++] = i;
        }
        
        return arr;
    }
}

Version 2: Using a hash array

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        int[] hash1 = new int[1002];
        int[] hash2 = new int[1002];
        for(int i : nums1)
            hash1[i]++;
        for(int i : nums2)
            hash2[i]++;
        List<Integer> resList = new ArrayList<>();
        for(int i = 0; i < 1002; i++)
            if(hash1[i] > 0 && hash2[i] > 0)
                resList.add(i);
        int index = 0;
        int res[] = new int[resList.size()];
        for(int i : resList)
            res[index++] = i;
        return res;
    }
}

Python3:

Version 1: Using dictionary and set

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
    # Use hash table to store all elements from one array
        table = {}
        for num in nums1:
            table[num] = table.get(num, 0) + 1
        
        # Use a set to store the result
        res = set()
        for num in nums2:
            if num in table:
                res.add(num)
                del table[num]
        
        return list(res)

Version 2: Using an array

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        count1 = [0]*1001
        count2 = [0]*1001
        result = []
        for i in range(len(nums1)):
            count1[nums1[i]]+=1
        for j in range(len(nums2)):
            count2[nums2[j]]+=1
        for k in range(1001):
            if count1[k]*count2[k]>0:
                result.append(k)
        return result

Version 3: Using set

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        return list(set(nums1) & set(nums2))

Go

Version 1: Using dictionary and set

func intersection(nums1 []int, nums2 []int) []int {
    set:=make(map[int]struct{},0)  // Use map to simulate set
    res:=make([]int,0)
    for _,v:=range nums1{
        if _,ok:=set[v];!ok{
            set[v]=struct{}{}
        }
    }
    for _,v:=range nums2{
        // If element exists in previous array, add to result set and clear set value
        if _,ok:=set[v];ok{
            res=append(res,v)
            delete(set, v)
        }
    }
    return res
}

Version 2: Using an array

func intersection(nums1 []int, nums2 []int) []int {
    count1 := make([]int, 1001, 1001)
    count2 := make([]int, 1001, 1001)
    res := make([]int, 0)
    for _, v := range nums1 {
        count1[v] = 1
    }
    for _, v := range nums2 {
        count2[v] = 1
    }
    for i := 0; i <= 1000; i++ {
        if count1[i] + count2[i] == 2 {
            res = append(res, i)
        }
    }
    return res
}

JavaScript

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number[]}
 */
var intersection = function(nums1, nums2) {
    // Swap arrays based on size
    if(nums1.length < nums2.length) {
        const _ = nums1;
        nums1 = nums2;
        nums2 = _;
    }
    const nums1Set = new Set(nums1);
    const resSet = new Set();
    // Loop is faster than iterator
    for(let i = nums2.length - 1; i >= 0; i--) {
        nums1Set.has(nums2[i]) && resSet.add(nums2[i]);
    }
    return Array.from(resSet);
};

TypeScript

Version 1 (normal)

function intersection(nums1: number[], nums2: number[]): number[] {
    let resSet: Set<number> = new Set(),
        nums1Set: Set<number> = new Set(nums1);
    for (let i of nums2) {
        if (nums1Set.has(i)) {
            resSet.add(i);
        }
    }
    return Array.from(resSet);
};

Version 2 (fancy)

function intersection(nums1: number[], nums2: number[]): number[] {
    return Array.from(new Set(nums1.filter(i => nums2.includes(i))))
};

Swift

func intersection(_ nums1: [Int], _ nums2: [Int]) -> [Int] {
    var set1 = Set<Int>()
    var set2 = Set<Int>()
    for num in nums1 {
        set1.insert(num)
    }
    for num in nums2 {
        if set1.contains(num) {
            set2.insert(num)
        }
    }
    return Array(set2)
}

PHP

class Solution {
    /**
     * @param Integer[] $nums1
     * @param Integer[] $nums2
     * @return Integer[]
     */
    function intersection($nums1, $nums2) {
        if (count($nums1) == 0 || count($nums2) == 0) {
            return [];
        }
        $counts = [];
        $res = [];
        foreach ($nums1 as $num) {
            $counts[$num] = 1;
        }
        foreach ($nums2 as $num) {
            if (isset($counts[$num])) {
                $res[] = $num;
            }
            unset($counts[$num]);
        }
        
        return $res;
    }
}

Rust

use std::collections::HashSet;
impl Solution {
    pub fn intersection(nums1: Vec<i32>, nums2: Vec<i32>) -> Vec<i32> {
        let mut resultSet: HashSet<i32> = HashSet::with_capacity(1000);
        let nums1Set: HashSet<i32> = nums1.into_iter().collect();
        
        for num in nums2.iter() {
            if nums1Set.contains(num) {
                resultSet.insert(*num);
            }          
        }
        
        let ret: Vec<i32> = resultSet.into_iter().collect();
        ret
    }
}

Alternative solution:

use std::collections::HashSet;
impl Solution {
    pub fn intersection(nums1: Vec<i32>, nums2: Vec<i32>) -> Vec<i32> {
        nums1
            .into_iter()
            .collect::<HashSet<_>>()
            .intersection(&nums2.into_iter().collect::<HashSet<_>>())
            .copied()
            .collect()
    }
}

C

int* intersection1(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize){

    int nums1Cnt[1000] = {0};
    int lessSize = nums1Size < nums2Size ? nums1Size : nums2Size;
    int * result = (int *) calloc(lessSize, sizeof(int));
    int resultIndex = 0;
    int* tempNums;
    
    int i;

    /* Calculate the number's counts for nums1 array */
    for(i = 0; i < nums1Size; i ++) {
        nums1Cnt[nums1[i]]++;
    }

    /* Check if the value in nums2 is existing in nums1 count array */
    for(i = 0; i < nums2Size; i ++) {
        if(nums1Cnt[nums2[i]] > 0) {
            result[resultIndex] = nums2[i];
            resultIndex ++;
            /* Clear this count to avoid duplicated value */
            nums1Cnt[nums2[i]] = 0;
        }
    }
    * returnSize = resultIndex;
    return result;
}

Scala

Normal version:

object Solution {
  def intersection(nums1: Array[Int], nums2: Array[Int]): Array[Int] = {
    // Import mutable
    import scala.collection.mutable
    // Temporary Set to record each element in array1
    val tmpSet: mutable.HashSet[Int] = new mutable.HashSet[Int]()
    // Result Set to store the final result
    val resSet: mutable.HashSet[Int] = new mutable.HashSet[Int]()
    // Traverse through nums1 and add each element to tmpSet
    nums1.foreach(tmpSet.add(_))
    // Traverse through nums2 and add to resSet if it exists in tmpSet
    nums2.foreach(elem => {
      if (tmpSet.contains(elem)) {
        resSet.add(elem)
      }
    })
    // Convert result to Array and return it
    resSet.toArray
  }
}

Fancy version 1:

object Solution {
  def intersection(nums1: Array[Int], nums2: Array[Int]): Array[Int] = {
    // Convert to Set, get intersection, then convert to Array
    (nums1.toSet).intersect(nums2.toSet).toArray
  }
}

Fancy version 2:

object Solution {
  def intersection(nums1: Array[Int], nums2: Array[Int]): Array[Int] = {
    // De-duplicate and then get intersection
    (nums1.distinct).intersect(nums2.distinct)
  }
}

C#

 public int[] Intersection(int[] nums1, int[] nums2) {
    if(nums1==null||nums1.Length==0||nums2==null||nums1.Length==0)
    	return new int[0]; // Note array condition
    HashSet<int> one = Insert(nums1);
    HashSet<int> two = Insert(nums2);
    one.IntersectWith(two);
    return one.ToArray();
	}
 public HashSet<int> Insert(int[] nums){
    HashSet<int> one = new HashSet<int>();
    foreach(int num in nums){
    	one.Add(num);         
    	}
        return one;
	}

Ruby

def intersection(nums1, nums2)
  hash = {}
  result = {}

  nums1.each do |num|
    hash[num] = 1 if hash[num].nil?
  end

  nums2.each do |num|
    # Take the intersection of nums1 and nums2
    result[num] = 1 if hash[num] != nil
  end

  return result.keys
end

Related Problems

• 350. Intersection of Two Arrays II (opens new window)