# 1791. Find Center of Star Graph

Problem Link (opens new window)

The approach to this problem is to count the degree of each node (there is no distinction between in-degree and out-degree here), and if a node's degree equals the number of edges in this graph, then it must be the center node.

What is degree? It can be understood as the number of edges connected to a node. The degree in the problem is shown as:

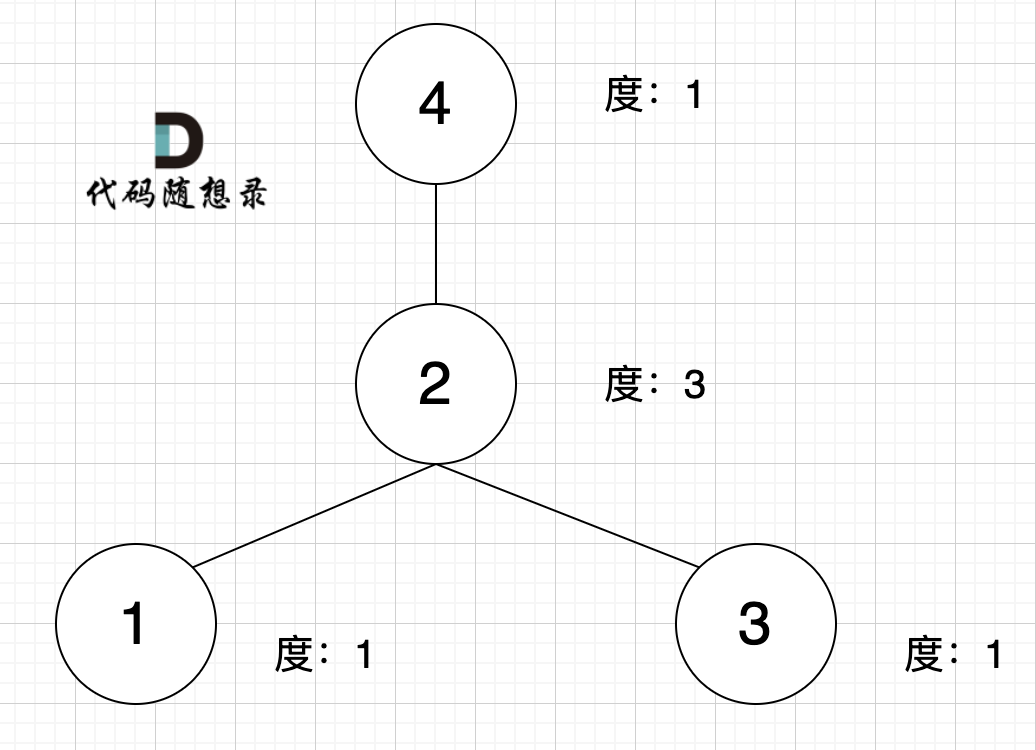
1791. Find Center of Star Graph

As for out-degree and in-degree, they are concepts in directed graphs. This problem involves an undirected graph.

Here is the code for this problem:


class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        unordered_map<int, int> du;
        for (int i = 0; i < edges.size(); i++) { // Count the degree of each node
            du[edges[i][1]]++;
            du[edges[i][0]]++;
        }
        unordered_map<int, int>::iterator iter; // Find the node with degree equal to the number of edges
        for (iter = du.begin(); iter != du.end(); iter++) {
            if (iter->second == edges.size()) return iter->first;
        }
        return -1;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

In fact, you can record the degree without counting at the end because the problem states that it is definitely a star graph. Thus, once a node's degree is greater than 1, you can return that node's value accordingly, as only the central node's degree will be greater than 1.

Here's a more concise code:

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        vector<int> du(edges.size() + 2);  // edges.size() + 1 is the number of nodes, the index represents the node number, so +2
        for (int i = 0; i < edges.size(); i++) {
            du[edges[i][1]]++;
            du[edges[i][0]]++;
            if (du[edges[i][1]] > 1) return edges[i][1];
            if (du[edges[i][0]] > 1) return edges[i][0];
        }
        return -1;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13

In the above code, unordered_map was not used, as creating new space during traversal can waste time. Instead, a vector was used, which is a strategy to trade space for time.

The code can be further simplified:

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        vector<int> du(edges.size() + 2);
        for (int i = 0; i < edges.size(); i++) {
            if (++du[edges[i][1]] > 1) return edges[i][1];
            if (++du[edges[i][0]] > 1) return edges[i][0];
        }
        return -1;
    }
};

1
2
3
4
5
6
7
8
9
10
11