Intersection of Two Linked Lists

Problem Description

Given two (singly) linked lists, determine if the two lists intersect. Return the node of intersection. Note that the intersection is defined based on reference, not value. That is, if the kth node of the first linked list is the exact same node (by reference) as the jth node of the second linked list, they are considered intersecting.

Example

Example 1

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value 8
Input Explanation: The intersected node's value is 8 (note that the node itself has a reference in the memory). From the start of the linked lists shown by listA and listB, the node is found at position 2 and position 3, respectively.

Example 2

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value 2
Input Explanation: The intersected node's value is 2. The node itself is found at position 3 of listA and position 1 of listB.

Example 3

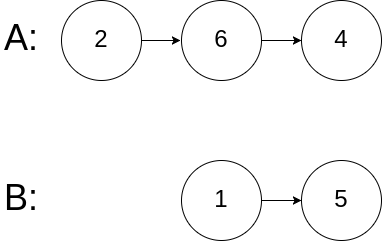
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Input Explanation: In this case, the two lists do not intersect, and thus the output is null.

Constraints

• The number of nodes in each linked list is within the range [0, 10^4].
• The value of each node is a unique integer within the range [1, 10^5].
• The problem guarantees that at most one intersection exists between the two lists.

Solutions

Method 1: Hash Table Method

The most intuitive method is to use a hash table for storage. We can store all the nodes visited in listA using a hash set, and then check the second list, listB.

• Traverse listA and store each node reference in a hash set.
• Traverse listB. If a node is found in the hash set, it means that at this node listA and listB intersect; output this node.
• If listB does not find an intersecting node after traversal, return null.

Method 2: Two Pointer Method

We can use the two-pointer technique to traverse the two lists and find the intersection node at constant space cost.

1. Initialize two pointers, p1 and p2, starting at the heads of list A and list B, respectively.
2. Move both pointers forward at the same pace, i.e., one step at a time.
3. On meeting the end of a list, redirect the pointer to the head of the other list:
   • If p1 has reached the end of list A, redirect it to the head of list B.
   • If p2 has reached the end of list B, redirect it to the head of list A.
4. If both lists are the same length, p1 and p2 will either simultaneously become null or meet at the intersection node.
5. If one list is longer than the other, both pointers will eventually meet at a single node concurrently. This node is the intersection node.

Note:

• The switching of pointers ensures that the time taken to traverse listA combined with the remaining traversal of listB equals the time taken to traverse listB combined with the remaining traversal of listA. This works because any point of intersection follows the same traversal pattern for both pointers after sufficient initial traversal.
• If there is no intersection, the above mechanism will yield a simultaneous null meeting point, i.e., termination of traversal for both pointers.

Conclusion

Understanding the "Intersection of Two Linked Lists" problem provides insight into detecting intersections efficiently using different techniques. By leveraging hash tables or two-pointer techniques, the solution can adaptively fit different scenarios with varied complexities. The two-pointer technique offers a unique O(n) time complexity approach with O(1) space complexity, making it an efficient solution when working with large lists.