Finding if there's a cycle is already challenging, and now you want me to find the entry point of the cycle?
# 142. Linked List Cycle II
LeetCode Problem Link (opens new window)
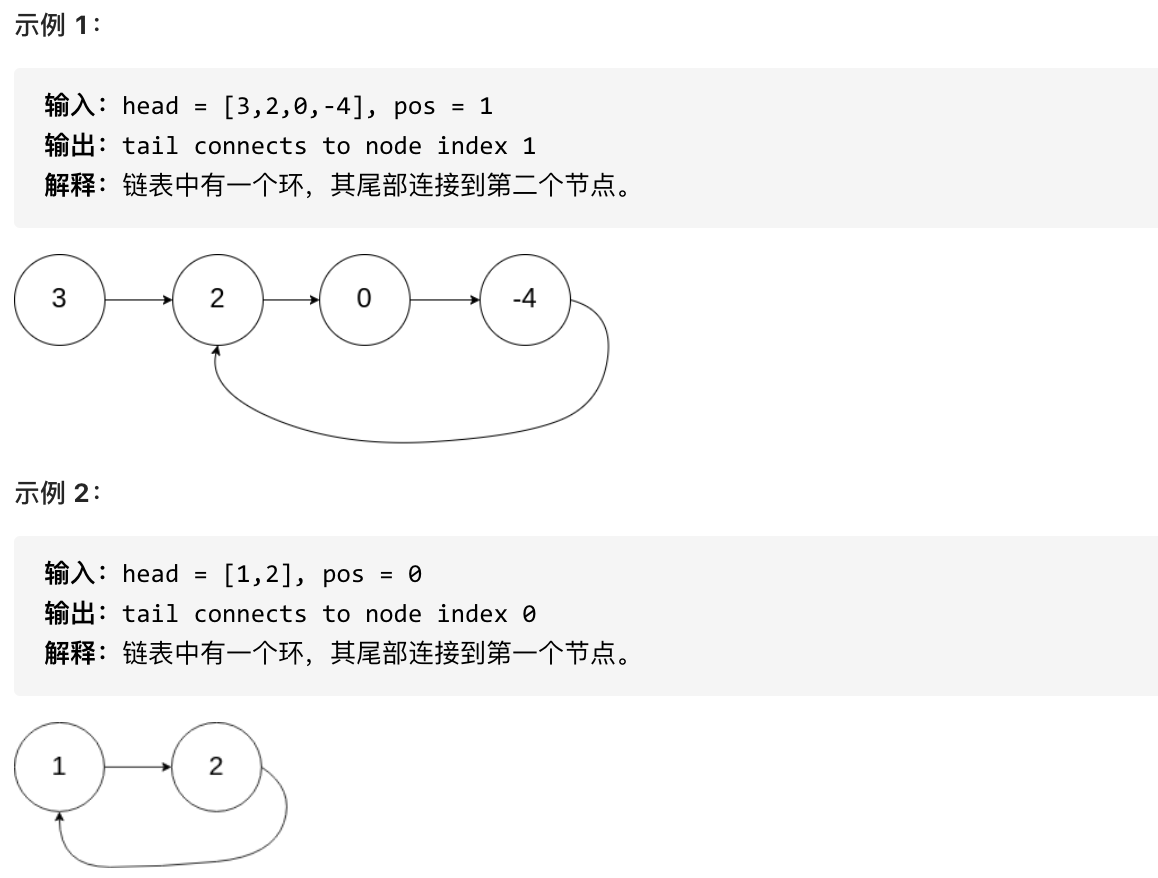
Problem Statement: Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where the tail connects to. If pos is -1, then there is no cycle in the link list.
Note: Do not modify the linked list.
# Approach
This problem tests both linked list manipulation and some mathematical reasoning.
The main concepts being tested are:
- Determining if a linked list has a cycle
- If a cycle exists, finding the entry point of the cycle
# Determining if a Linked List has a Cycle
You can use the fast and slow pointer method by defining fast and slow pointers. Start both from the head node, with fast moving two steps at a time and slow moving one. If there is a cycle, fast and slow will eventually meet inside the cycle.
Why do fast and slow pointers meet in the cycle and not miss each other indefinitely?
First, point out: The fast pointer will definitely enter the cycle first, and if fast and slow meet, it must be inside the cycle.
Then explain: Why will fast and slow definitely meet inside the cycle?
Visualize any cycle where the fast pointer starts to chase the slow pointer. Ultimately, this results in the following scenario:

When fast and slow both move one more step each, they meet.
This happens because, relative to the slow, the fast is moving one node closer each time, ensuring it eventually overlaps with slow.
The animation is as follows:

# Finding the Entry Point of the Cycle
Once you determine there is a cycle, the next step is finding where the cycle begins.
Assume the number of nodes from the head to the cycle entry node is x. The number of nodes from the cycle entry node to the meeting point of fast and slow is y. Let the number of nodes from the meeting point back to the cycle entry node be z. As shown:

When fast and slow meet:
The number of nodes slow has traveled: x + y,
The number of nodes fast has traveled: x + y + n(y + z), where n is the number of cycles fast has completed before meeting slow, and y+z is the number of nodes per cycle.
Since fast moves two steps for every step slow moves, thus:
(x + y) * 2 = x + y + n(y + z)
Cancel out one (x + y) from both sides:
x + y = n(y + z)
To find x (the distance from the head to the cycle's entry point), isolate x:
x = n(y + z) - y
Factor out an (y + z) from n(y + z) and rearrange:
x = (n - 1)(y + z) + z
Note here, n is at least 1, since fast must complete at least one full cycle before catching up with slow.
This indicates that starting a pointer from the head and another from the meeting point, both walking one node at a time, will lead them to meet at the entry point of the cycle.
Thus, define a pointer index1 at the meeting point, and another pointer index2 at the head.
Let index1 and index2 move simultaneously, one node at a time. Their meeting point will be the node where the cycle starts.
The animation is as follows:
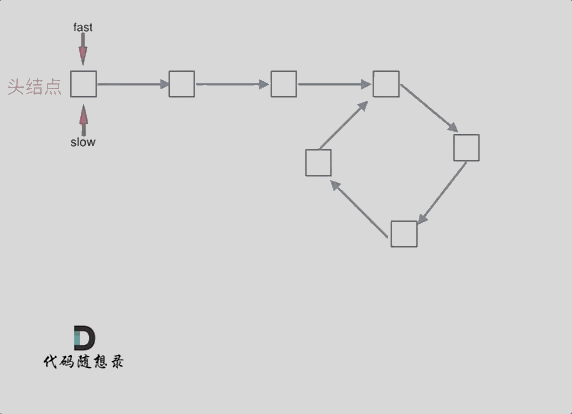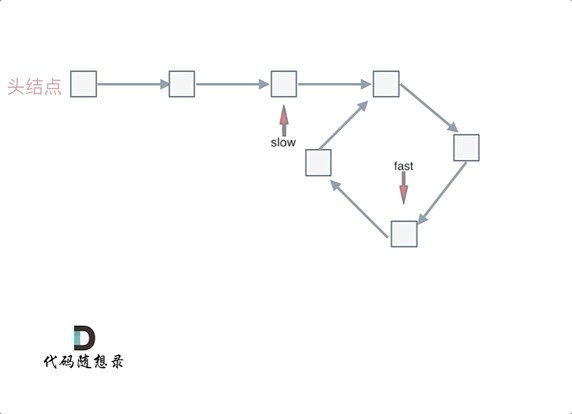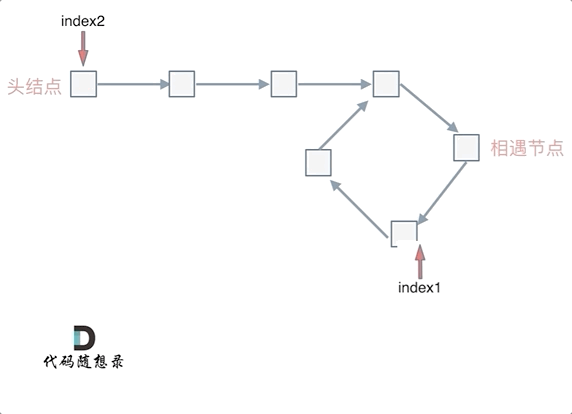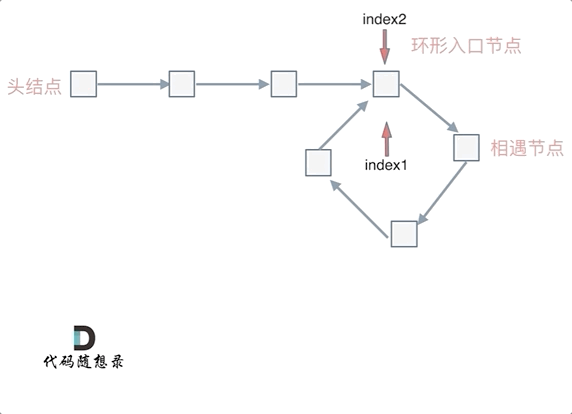
Now, if n is more than 1, it means fast has completed n laps in the circle before catching up with slow. However, this method still works in all situations, as index1 only traverses (n-1) additional cycles before meeting index2, which will be at the cycle start.
The code is as follows:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// When fast and slow pointers meet, start searching from head and the meeting point
if (slow == fast) {
ListNode* index1 = fast;
ListNode* index2 = head;
while (index1 != index2) {
index1 = index1->next;
index2 = index2->next;
}
return index2; // Return cycle entry point
}
}
return NULL;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
- Time Complexity: O(n), as the number of steps before the fast and slow pointers meet is less than the list length, and additional steps taken by
index1andindex2are also less than the list length, summing up to less than2n. - Space Complexity: O(1)
# Supplement
During the process, you might wonder: Why, upon first meeting inside the cycle, is the number of steps slow has moved just x + y instead of x + some full cycles + y?
Refer to the article Linked List: Finding the Cycle, Now Where’s the Entry? (opens new window) for more clarity on the following:
Assume when the slow enters the cycle, fast is already in the cycle.
If both slow and fast start together at the cycle entry, imagine the cycle as a straight line:
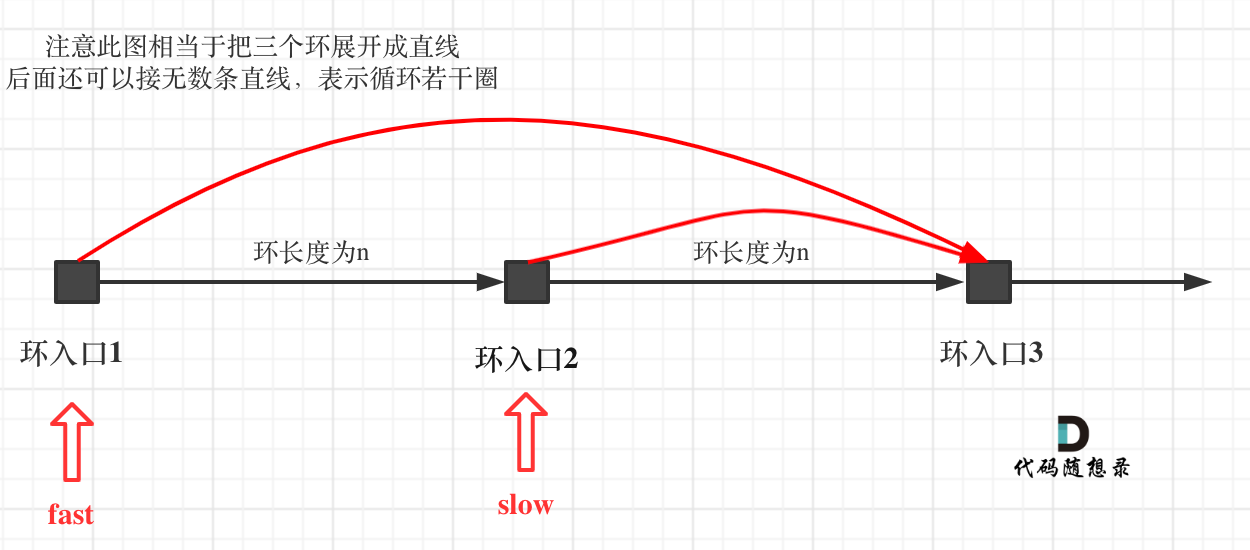
It's evident that slow and fast meet at the entry point 3, with slow having traversed one cycle and fast two cycles.
Now here's the key: Fast is somewhere in the cycle when slow begins, as shown:

Then by the time fast reaches entry 3, it has already covered k + n steps. Slow, subsequently, has covered(k + n) / 2` steps.
Given k < n (as visualized), (k + n) / 2 is always less than n.
This implies slow must intersect with fast during this initial cycle.
And why can’t fast skip over slow? As clarified earlier, relative to slow, fast moves towards slow one step at a time, so it cannot skip over.
This fully explains why slow's steps add up to x + y and not x + several full cycles + y, complementing Linked List: Finding the Cycle, Now Where’s the Entry? (opens new window).
# Conclusion
This in-depth analysis and mathematical reasoning complete a comprehensive explanation of solving this circular linked list problem.
# Versions in Other Languages
# Java:
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {// Has cycle
ListNode index1 = fast;
ListNode index2 = head;
// Both pointers walk step-by-step and meet at the cycle entry
while (index1 != index2) {
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
return null;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Python:
# Version 1: Fast and Slow Pointers
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# If there is a cycle, the slow and fast pointers will eventually meet
if slow == fast:
# Move one of the pointers back to the start of the list
slow = head
while slow != fast:
slow = slow.next
fast = fast.next
return slow
# If there is no cycle, return None
return None
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Version 2: Using a Set
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
visited = set()
while head:
if head in visited:
return head
visited.add(head)
head = head.next
return None
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Go:
func detectCycle(head *ListNode) *ListNode {
slow, fast := head, head
for fast != nil && fast.Next != nil {
slow = slow.Next
fast = fast.Next.Next
if slow == fast {
for slow != head {
slow = slow.Next
head = head.Next
}
return head
}
}
return nil
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# JavaScript
// Two ways to implement the loop
/**
* @param {ListNode} head
* @return {ListNode}
*/
// First determine whether it's a circular linked list
var detectCycle = function(head) {
if(!head || !head.next) return null;
let slow =head.next, fast = head.next.next;
while(fast && fast.next && fast!== slow) {
slow = slow.next;
fast = fast.next.next;
}
if(!fast || !fast.next ) return null;
slow = head;
while (fast !== slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
};
var detectCycle = function(head) {
if(!head || !head.next) return null;
let slow =head.next, fast = head.next.next;
while(fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
if(fast == slow) {
slow = head;
while (fast !== slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
return null;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# TypeScript:
function detectCycle(head: ListNode | null): ListNode | null {
let slowNode: ListNode | null = head,
fastNode: ListNode | null = head;
while (fastNode !== null && fastNode.next !== null) {
slowNode = slowNode!.next;
fastNode = fastNode.next.next;
if (slowNode === fastNode) {
slowNode = head;
while (slowNode !== fastNode) {
slowNode = slowNode!.next;
fastNode = fastNode!.next;
}
return slowNode;
}
}
return null;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Swift:
class Solution {
func detectCycle(_ head: ListNode?) -> ListNode? {
var slow: ListNode? = head
var fast: ListNode? = head
while fast != nil && fast?.next != nil {
slow = slow?.next
fast = fast?.next?.next
if slow == fast {
// Meeting in the cycle
var list1: ListNode? = slow
var list2: ListNode? = head
while list1 != list2 {
list1 = list1?.next
list2 = list2?.next
}
return list2
}
}
return nil
}
}
extension ListNode: Equatable {
public func hash(into hasher: inout Hasher) {
hasher.combine(val)
hasher.combine(ObjectIdentifier(self))
}
public static func == (lhs: ListNode, rhs: ListNode) -> Bool {
return lhs === rhs
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# C:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while (fast && fast->next) {
// Check if pointers are equal before moving them (prevent skipping)
slow = slow->next;
fast = fast->next->next;
if (slow == fast) { // intersect, start searching for cycle entry
ListNode *f = fast, *h = head;
while (f != h) f = f->next, h = h->next;
return h;
}
}
return NULL;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# Scala:
object Solution {
def detectCycle(head: ListNode): ListNode = {
var fast = head // fast pointer
var slow = head // slow pointer
while (fast != null && fast.next != null) {
fast = fast.next.next // fast pointer moves two steps
slow = slow.next // slow pointer moves one step
// if intersect, fast pointer restarts from head
if (fast == slow) {
fast = head
// both pointers move step-by-step, meeting at cycle entry point
while (fast != slow) {
fast = fast.next
slow = slow.next
}
return fast
}
}
// if fast reaches null, there is no cycle, return null
null
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C#:
public class Solution
{
public ListNode DetectCycle(ListNode head)
{
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null)
{
slow = slow.next;
fast = fast.next.next;
if (fast == slow)
{
fast = head;
while (fast != slow)
{
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
