# 42. Trapping Rain Water
LeetCode Problem Link (opens new window)
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
Example 1:

- Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
- Output: 6
- Explanation: The elevation map represented by array [0,1,0,2,1,0,1,3,2,1,2,1] can trap 6 units of rainwater (the blue section).
Example 2:
- Input: height = [4,2,0,3,2,5]
- Output: 9
# Approach
The trapping rainwater problem is quite common in interviews, and it's essential to discuss it thoroughly.
In this article, we will delve into three approaches:
- Brute Force Solution
- Optimized Two-Pointer Solution
- Monotonic Stack
# Brute Force
The brute force solution also uses the two-pointer technique.
First, it's crucial to clarify whether to calculate by rows or by columns.
Calculating by rows as shown:

Calculating by columns as shown:
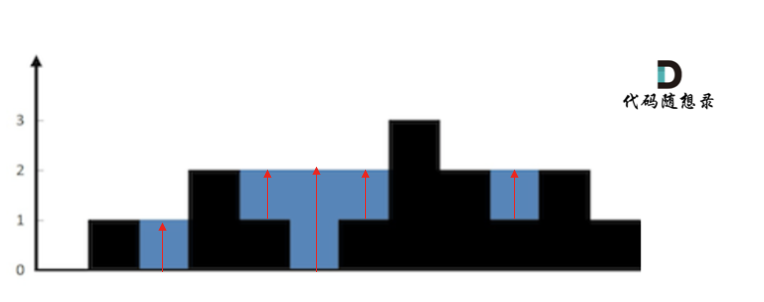
Some might find it confusing to switch between row and column calculations, causing increasing complexity as you write.
Personally, I prefer calculating by columns as it's relatively easier to comprehend. Let's take a closer look at calculating by columns.
Firstly, if calculated by columns, the width is always 1, then calculate the height of the rainwater for each column.
Each column's rainwater height depends on the tallest bars on the left and right of that column and the shorter of those two heights.
This description might be a little confusing, so here's an example: consider the rainwater height of column 4, as illustrated:
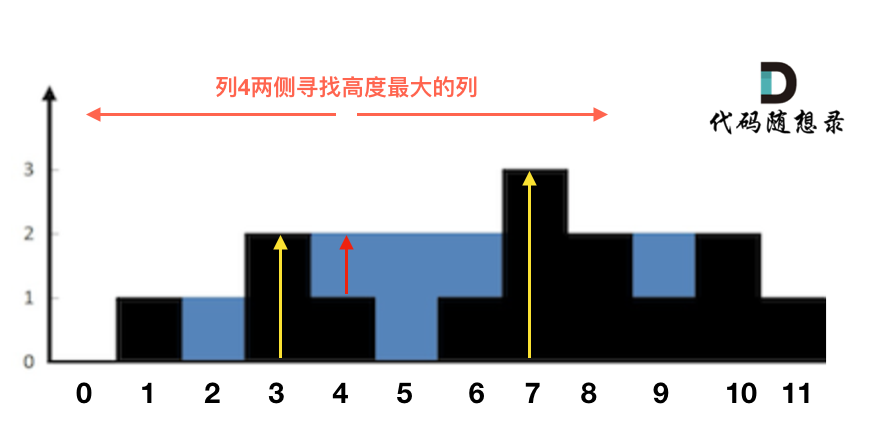
For column 4, the tallest bar to the left is column 3, with a height of 2 (denoted as lHeight).
For column 4, the tallest bar to the right is column 7, with a height of 3 (denoted as rHeight).
The height of the bar at column 4 is 1 (denoted as height).
Therefore, the height of the rainwater at column 4 is the minimum of lHeight and rHeight minus the height of column 4, i.e., min(lHeight, rHeight) - height.
The rainwater height for column 4 is then determined, and with a width of 1, the rainwater volume in column 4 is computed.
Thus, we've calculated the rainwater volume for column 4.
Using the same approach, if we traverse through all the columns and compute the water volume at each column, summing them yields the total volume of trapped rainwater.
We'll loop through all the columns and note that the first and the last columns do not trap any water:
for (int i = 0; i < height.size(); i++) {
// The first and last bars do not trap water
if (i == 0 || i == height.size() - 1) continue;
}
2
3
4
Within the loop, calculate the tallest bars both on the left and right:
int rHeight = height[i]; // Record the highest bar on the right
int lHeight = height[i]; // Record the highest bar on the left
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
2
3
4
5
6
7
8
Finally, calculate the rainwater height for that column:
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // Add to sum only if h is positive
2
The complete code looks like this:
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// The first and last bars do not trap water
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // Record the highest bar on the right
int lHeight = height[i]; // Record the highest bar on the left
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Since each column traversal requires examining the tallest columns on both sides, the time complexity is O(n^2), and the space complexity is O(1).
Later, LeetCode updated its backend test data, causing the above brute force solution to time out.
# Optimized Two-Pointer
In the brute force solution, we observe that we can calculate the water over each position using the concept of the tallest bar on the left and on the right. This represents column-based calculation.
Current column water height: min(left side tallest, right side tallest) - current bar height.
To determine the maximum height on both sides, we employed double pointers, evaluating both directions for each bar, leading to redundant computations. By keeping an array to record the maximum left height at each position (maxLeft) and another array to track the maximum right height (maxRight), we can avoid redundant calculations.
For the current position, the maximum height to the left is the maximum of the previous position's left height and the current height.
From left to right traversal: maxLeft[i] = max(height[i], maxLeft[i - 1]);
From right to left traversal: maxRight[i] = max(height[i], maxRight[i + 1]).
The code is as follows:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0;
vector<int> maxLeft(height.size(), 0);
vector<int> maxRight(height.size(), 0);
int size = maxRight.size();
// Record the maximum height of the bar to the left of each column
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// Record the maximum height of the bar to the right of each column
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// Calculate the total
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Monotonic Stack Solution
Regarding the basics of a monotonic stack, when it is suitable for solving problems, and its work process, please refer to the problem explanation 0739.Daily Temperatures (opens new window).
A monotonic stack maintains an ordered stack. Just like the Stack and Queue: Monotonic Queue (opens new window), we need to maintain ascending or descending order ourselves, as there is no ready-made container available.
Typically, a monotonic stack is used for a one-dimensional array, to find the position of the first element larger or smaller than the current element on the right or the left.
For the rainwater trapping problem, we need to find both the tallest elements to the left and right of the current position to determine the water trapped.
# Preparations
This problem has the following aspects when applying a monotonic stack:
- The monotonic stack computes water by row:

Understanding this helps with comprehension of the process.
- The order of elements in the monotonic stack:
Is it from largest to smallest, or smallest to largest?
The sequence from the stack head (where elements are popped) to the stack bottom should be from smallest to largest.
When an element added has a greater height than the stack head, a trough is formed. The stack head becomes the bottom of the trough, the second element of the stack is the left side, and the new element is the right side of the trough.
Illustrated as:
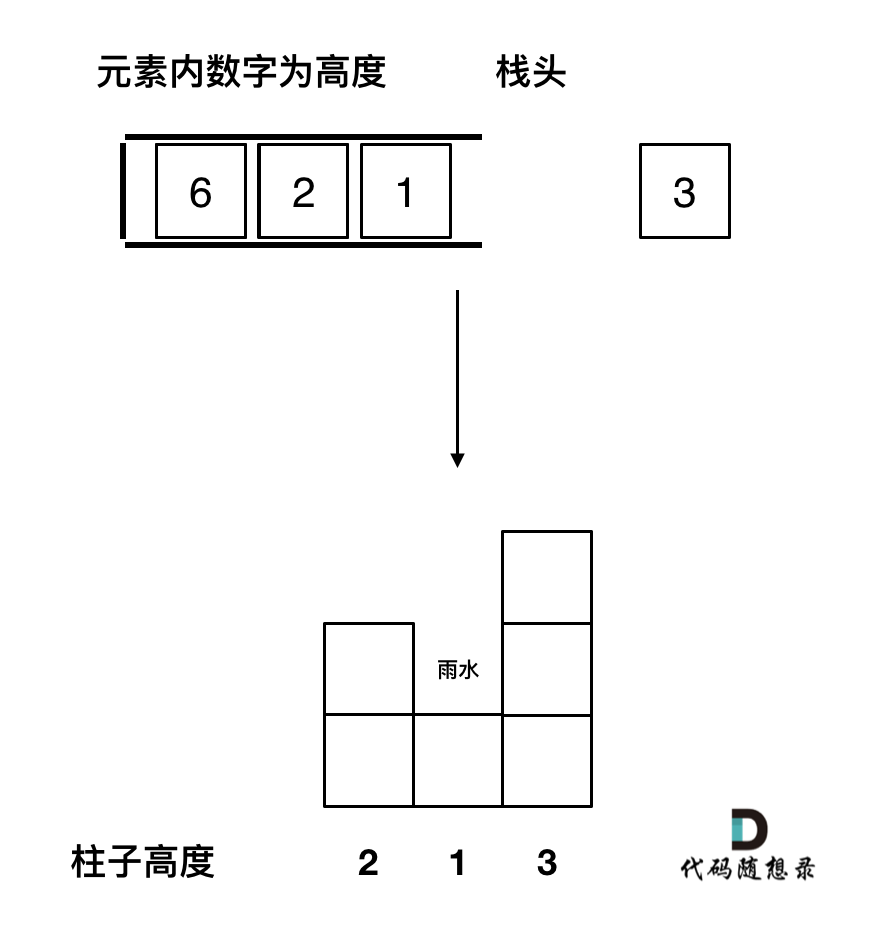
For the order of a monotonic stack, here's a summary: In 0739.Daily Temperatures (opens new window) problems, the monotonic stack is increasing when finding the first larger element on the right, while in 0084.Largest Rectangle in Histogram (opens new window), it is decreasing when finding the first smaller element on the right.
- What if two bars have the same height?
If two elements have the same height, update the stack by popping the old index and adding the new one.
For example, with 5 5 1 3, when adding the second 5, pop the first 5 and add the second 5 instead.
It's crucial because using the rightmost bar for width calculation is necessary for bars with the same height.
Illustrated as:
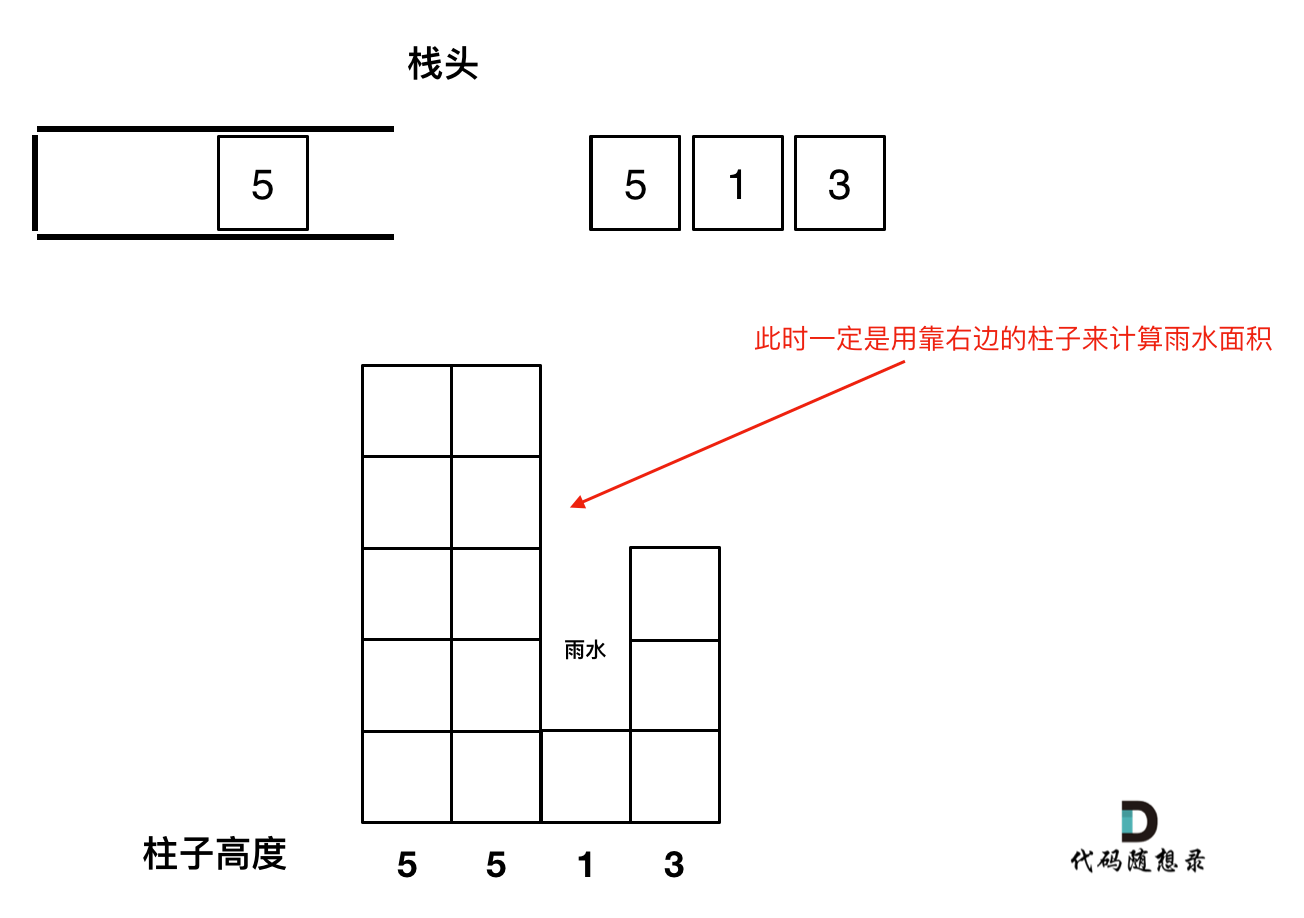
- What should be stored in the stack?
A monotonic stack also calculates water area by height * width.
The heights are determined by the columns' heights, and the widths by the columns' indices.
Is it necessary to store a pair<int, int> type element in the stack, with height and index of the bar?
Not really. Just store the indices, and the corresponding height can be accessed by height[stack.top()] using the popped index.
Hence, the stack is defined as:
stack<int> st; // Stores indices, using the indices to calculate the heights of bars.
After understanding these points, let's explore the processing logic.
# Monotonic Stack Processing Logic
The following process is similar to 0739.Daily Temperatures (opens new window), suggested to attempt 0739 Daily Temperatures (opens new window) prior.
The primary logic involves three scenarios:
- Scenario 1: Current element's (bar's) height is less than the stack's top height
height[i] < height[stack.top()] - Scenario 2: Current element's (bar's) height equals the stack's top height
height[i] == height[stack.top()] - Scenario 3: Current element's (bar's) height is greater than the stack's top height
height[i] > height[stack.top()]
Begin by adding the index of bar 0 to the stack with st.push(0);. As we are managing what we have traversed, we add index 0 first.
Then, proceed by traversing from index 1 with for (int i = 1; i < height.size(); i++).
If the current element has a height less than the stack head, add the element, conforming to the order of smallest to largest (stack head to base).
if (height[i] < height[st.top()]) st.push(i);
If it equals the stack top, update the stack head because the latest position helps determine the width when two bars are of equal height:
if (height[i] == height[st.top()]) { // Example: 5 5 1 7
st.pop();
st.push(i);
}
2
3
4
In cases of a greater current height forming a trough, use stack head, second from the top, and the new element to calculate:
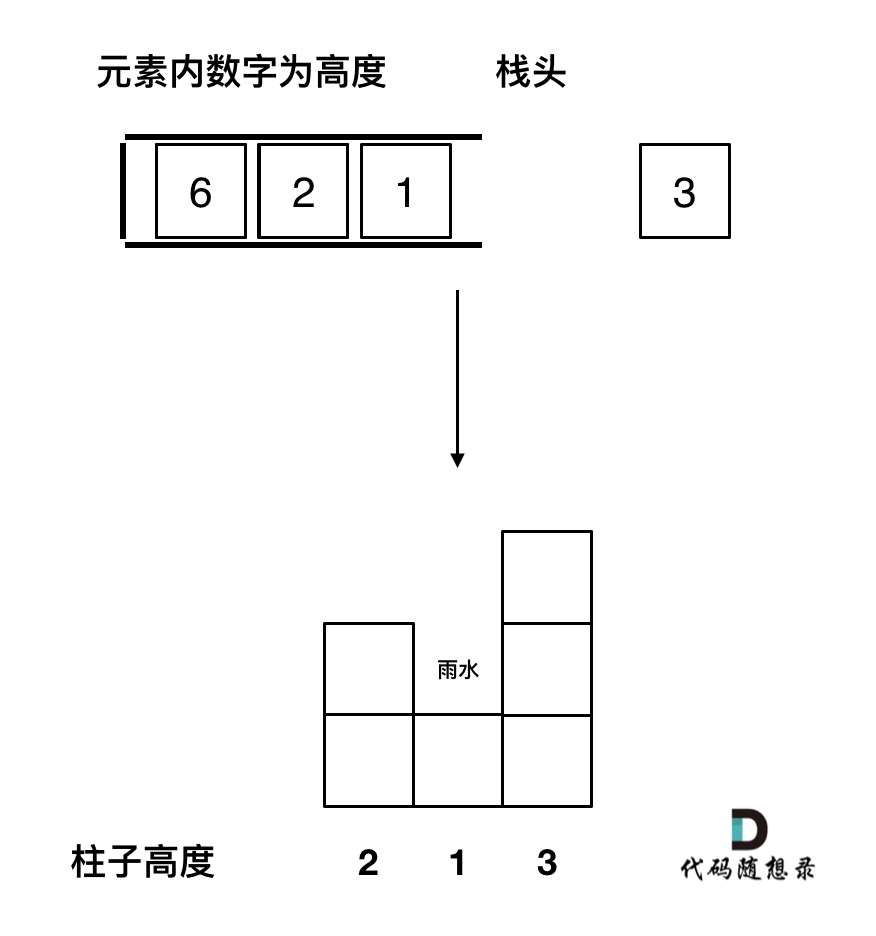
Pop the stack's top to retrieve the trough's base, height of height[mid], and record the trough's right and left edges from the stack top and index i.
Water height: min(Left height, Right height) - base height.
Water width: Right index - Left index - 1.
Calculate trough water volume: h * w.
Code snippet for current trough's water volume:
while (!st.empty() && height[i] > height[st.top()]) { // Note while for continuous stack top update
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // Only calculate the width
sum += h * w;
}
}
2
3
4
5
6
7
8
9
Critical part explained, complete code:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0; // Can be omitted
stack<int> st; // Stores indices using height of those indices
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // Situation 1
st.push(i);
} if (height[i] == height[st.top()]) { // Situation 2
st.pop(); // That line can be omitted with the same effect, but changes the logic.
st.push(i);
} else { // Situation 3
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
For a streamlined version:
class Solution {
public:
int trap(vector<int>& height) {
stack<int> st;
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
In the streamlined version, you might lose insight into the three scenarios but gain compactness with fused logic through situations one and two. This version can obscure understanding.
# Other Language Versions
# Java:
Brute Force:
class Solution {
public int trap(int[] height) {
int sum = 0;
for (int i = 0; i < height.length; i++) {
// The first and last bars do not trap water
if (i==0 || i== height.length - 1) continue;
int rHeight = height[i]; // Record the highest bar on the right
int lHeight = height[i]; // Record the highest bar on the left
for (int r = i+1; r < height.length; r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i-1; l >= 0; l--) {
if(height[l] > lHeight) lHeight = height[l];
}
int h = Math.min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Two-Pointer:
class Solution {
public int trap(int[] height) {
int length = height.length;
if (length <= 2) return 0;
int[] maxLeft = new int[length];
int[] maxRight = new int[length];
// Record the maximum height of the bar to the left of each column
maxLeft[0] = height[0];
for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
// Record the maximum height of the bar to the right of each column
maxRight[length - 1] = height[length - 1];
for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);
// Calculate the total
int sum = 0;
for (int i = 0; i < length; i++) {
int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Optimized Two-Pointer:
class Solution {
public int trap(int[] height) {
if (height.length <= 2) {
return 0;
}
// From both sides seeking both max
int maxLeft = height[0], maxRight = height[height.length - 1];
int l = 1, r = height.length - 2;
int res = 0;
while (l <= r) {
// Update both as it is uncertain whether the last move was on the left or on the right
maxLeft = Math.max(maxLeft, height[l]);
maxRight = Math.max(maxRight, height[r]);
// Move on the smaller side, as it is settled regarding the other side
if (maxLeft < maxRight) {
res += maxLeft - height[l ++];
} else {
res += maxRight - height[r --];
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Monotonic Stack:
class Solution {
public int trap(int[] height){
int size = height.length;
if (size <= 2) return 0;
Stack<Integer> stack = new Stack<Integer>();
stack.push(0);
int sum = 0;
for (int index = 1; index < size; index++){
int stackTop = stack.peek();
if (height[index] < height[stackTop]){
stack.push(index);
}else if (height[index] == height[stackTop]){
stack.pop();
stack.push(index);
}else{
while (!stack.isEmpty() && (height[index] > height[stackTop])){
int mid = stack.pop();
if (!stack.isEmpty()){
int left = stack.peek();
int h = Math.min(height[left], height[index]) - height[mid];
int w = index - left - 1;
int hold = h * w;
if (hold > 0) sum += hold;
stackTop = stack.peek();
}
}
stack.push(index);
}
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Python:
Brute Force:
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
for i in range(len(height)):
if i == 0 or i == len(height)-1: continue
lHight = height[i-1]
rHight = height[i+1]
for j in range(i-1):
if height[j] > lHight:
lHight = height[j]
for k in range(i+2,len(height)):
if height[k] > rHight:
rHight = height[k]
res1 = min(lHight,rHight) - height[i]
if res1 > 0:
res += res1
return res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Two-Pointer:
class Solution:
def trap(self, height: List[int]) -> int:
leftheight, rightheight = [0]*len(height), [0]*len(height)
leftheight[0]=height[0]
for i in range(1,len(height)):
leftheight[i]=max(leftheight[i-1],height[i])
rightheight[-1]=height[-1]
for i in range(len(height)-2,-1,-1):
rightheight[i]=max(rightheight[i+1],height[i])
result = 0
for i in range(0,len(height)):
summ = min(leftheight[i],rightheight[i])-height[i]
result += summ
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Monotonic Stack:
class Solution:
def trap(self, height: List[int]) -> int:
# Monotonic Stack
'''
The monotonic stack computes by rows
From top to bottom: from small to large
Use three elements to trap water: the top of stack, the next in the stack, and the element to be pushed
Water height is `min(left height, right height) - trough base height`
Water width is `right index - left index - 1`
'''
# stack uses indices for bar heights
stack = [0]
result = 0
for i in range(1, len(height)):
# Case 1
if height[i] < height[stack[-1]]:
stack.append(i)
# Case 2
# For equal height bars, select the rightmost for width
elif height[i] == height[stack[-1]]:
stack.pop()
stack.append(i)
# Case 3
else:
while stack and height[i] > height[stack[-1]]:
mid = stack[-1]
stack.pop()
if stack:
right_height = height[i]
left_height = height[stack[-1]]
h = min(right_height, left_height) - height[mid]
w = i - stack[-1] - 1
result += h * w
stack.append(i)
return result
# Monotonic Stack, streamlined version
class Solution:
def trap(self, height: List[int]) -> int:
stack = [0]
result = 0
for i in range(1, len(height)):
while stack and height[i] > height[stack[-1]]:
mid = stack.pop()
if stack:
h = min(height[stack[-1]], height[i]) - height[mid]
w = i - stack[-1] - 1
result += h * w
stack.append(i)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# Go:
func trap(height []int) int {
var left, right, leftMax, rightMax, res int
right = len(height) - 1
for left < right {
if height[left] < height[right] {
if height[left] >= leftMax {
leftMax = height[left] // Set left max height
} else {
res += leftMax - height[left] // Add water trapped if bar shorter than left max
}
left++
} else {
if height[right] > rightMax {
rightMax = height[right] // Set right max height
} else {
res += rightMax - height[right] // Add water trapped if bar shorter than right max
}
right--
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Optimized Two-Pointer:
func trap(height []int) int {
sum:=0
n:=len(height)
lh:=make([]int,n)
rh:=make([]int,n)
lh[0]=height[0]
rh[n-1]=height[n-1]
for i:=1;i<n;i++{
lh[i]=max(lh[i-1],height[i])
}
for i:=n-2;i>=0;i--{
rh[i]=max(rh[i+1],height[i])
}
for i:=1;i<n-1;i++{
h:=min(rh[i],lh[i])-height[i]
if h>0{
sum+=h
}
}
return sum
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
func min(a,b int)int{
if a<b{
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Monotonic Stack:
func trap(height []int) int {
if len(height) <= 2 {
return 0
}
st := make([]int, 1, len(height))
var res int
for idx := 1; idx < len(height); idx++ {
stackTop := st[len(st)-1]
if height[idx] < height[stackTop] {
st = append(st, idx)
} else if height[idx] == height[stackTop] {
st = st[:len(st)-1]
st = append(st, idx)
} else {
while len(st) > 0 && height[idx] > height[stackTop] {
mid := st[len(st)-1]
st = st[:len(st)-1]
if len(st) > 0 {
h := (min(height[st[len(st)-1]], height[idx]) - height[mid]) * (idx - st[len(st)-1] - 1)
res += h
stackTop = st[len(st)-1]
}
}
st = append(st, idx)
}
}
return res
}
func min(x, y int) int {
if x >= y {
return y
}
return x
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Compressed Monotonic Stack:
func trap(height []int) int {
stack := make([]int, 0)
res := 0
// No need to push the first bar's index beforehand, it will be at the end of this loop
for i := 0; i < len(height); i++ {
for len(stack) > 0 && height[stack[len(stack)-1]] <= height[i] {
mid := stack[len(stack)-1]
stack = stack[:len(stack)-1]
if len(stack) > 0 {
h := min(height[stack[len(stack)-1]], height[i]) - height[mid]
w := i - stack[len(stack)-1] - 1
res += h * w
}
}
stack = append(stack, i)
}
return res
}
func min(x, y int) int {
if x < y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# JavaScript:
// Brute Force
var trap = function(height) {
const len = height.length;
let sum = 0;
for(let i = 0; i < len; i++){
if(i === 0 || i === len - 1) continue;
let rHeight = height[i];
let lHeight = height[i];
for(let r = i + 1; r < len; r++){
if(height[r] > rHeight) rHeight = height[r];
}
for(let l = i - 1; l >= 0; l--){
if(height[l] > lHeight) lHeight = height[l];
}
let h = Math.min(lHeight, rHeight) - height[i];
if(h > 0) sum += h;
}
return sum;
};
// Two-Pointer
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
const maxLeft = new Array(len).fill(0);
const maxRight = new Array(len).fill(0);
maxLeft[0] = height[0];
for(let i = 1; i < len; i++){
maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
}
maxRight[len - 1] = height[len - 1];
for(let i = len - 2; i >= 0; i--){
maxRight[i] = Math.max(height[i], maxRight[i + 1]);
}
let sum = 0;
for(let i = 0; i < len; i++){
let count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if(count > 0) sum += count;
}
return sum;
};
// Monotonic Stack with JS Array as Stack
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
const st = [];
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){
if(height[i] < height[st[st.length - 1]]){ // Case 1
st.push(i);
}
if (height[i] === height[st[st.length - 1]]) { // Case 2
st.pop();
st.push(i);
} else { // Case 3
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) {
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1;
sum += h * w;
}
}
st.push(i);
}
}
return sum;
};
// Simplified Monotonic Stack
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
const st = [];
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) {
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# TypeScript:
Brute Force:
function trap(height: number[]): number {
const length: number = height.length;
let resVal: number = 0;
for (let i = 0; i < length; i++) {
let leftMaxHeight: number = height[i],
rightMaxHeight: number = height[i];
let leftIndex: number = i - 1,
rightIndex: number = i + 1;
while (leftIndex >= 0) {
if (height[leftIndex] > leftMaxHeight)
leftMaxHeight = height[leftIndex];
leftIndex--;
}
while (rightIndex < length) {
if (height[rightIndex] > rightMaxHeight)
rightMaxHeight = height[rightIndex];
rightIndex++;
}
resVal += Math.min(leftMaxHeight, rightMaxHeight) - height[i];
}
return resVal;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Two-Pointer:
function trap(height: number[]): number {
const length: number = height.length;
const leftMaxHeightDp: number[] = [],
rightMaxHeightDp: number[] = [];
leftMaxHeightDp[0] = height[0];
rightMaxHeightDp[length - 1] = height[length - 1];
for (let i = 1; i < length; i++) {
leftMaxHeightDp[i] = Math.max(height[i], leftMaxHeightDp[i - 1]);
}
for (let i = length - 2; i >= 0; i--) {
rightMaxHeightDp[i] = Math.max(height[i], rightMaxHeightDp[i + 1]);
}
let resVal: number = 0;
for (let i = 0; i < length; i++) {
resVal += Math.min(leftMaxHeightDp[i], rightMaxHeightDp[i]) - height[i];
}
return resVal;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Monotonic Stack:
function trap(height: number[]): number {
const length: number = height.length;
const stack: number[] = [];
stack.push(0);
let resVal: number = 0;
for (let i = 1; i < length; i++) {
let top = stack[stack.length - 1];
if (height[top] > height[i]) {
stack.push(i);
} else if (height[top] === height[i]) {
stack.pop();
stack.push(i);
} else {
while (stack.length > 0 && height[top] < height[i]) {
let mid = stack.pop();
if (stack.length > 0) {
let left = stack[stack.length - 1];
let h = Math.min(height[left], height[i]) - height[mid];
let w = i - left - 1;
resVal += h * w;
top = stack[stack.length - 1];
}
}
stack.push(i);
}
}
return resVal;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# C:
A simpler two-pointer method:
The previous two-pointer approach fixed the position of the "base" and searched both directions for a higher "wall," looping several times to calculate the sum.
We can reverse the logic, using two pointers initialized at the start and end, representing "walls" pushed towards the center, maintaining each "base" having max "walls."
Essentially, it's changing the calculation direction, reducing redundant operations.
Code:
int trap(int* height, int heightSize) {
int ans = 0;
int left = 0, right = heightSize - 1; // Initialize pointers at both ends
int leftMax = 0, rightMax = 0; // Tracks highest walls
while (left < right) { // End when pointers meet
leftMax = fmax(leftMax, height[left]);
rightMax = fmax(rightMax, height[right]);
if (leftMax < rightMax) {
ans += leftMax - height[left]; // Traps water at the current base (left)
++left; // Moves the pointer on the smaller side, subject to constraints
} else {
ans += rightMax - height[right]; // Traps water at the base (right)
--right;
}
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time complexity: O(n)
- Space complexity: O(1)
# Rust:
Two-Pointer
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let n = height.len();
let mut max_left = vec![0; height.len()];
let mut max_right = vec![0; height.len()];
max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
let lmax = lm.max(height[idx]);
let rmax = rm.max(height[n - 1 - idx]);
*x = lmax; *y = rmax;
(lmax, rmax)
});
height.iter().enumerate().fold(0, |acc, (idx, x)| {
let h = max_left[idx].min(max_right[idx]);
if h > 0 { h - x + acc } else { acc }
})
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Monotonic Stack:
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let mut stack = vec![];
let mut ans = 0;
for (right_pos, &right_h) in height.iter().enumerate() {
while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
let mid_pos = stack.pop().unwrap();
if !stack.is_empty() {
let left_pos = *stack.last().unwrap();
let left_h = height[left_pos];
let top = std::cmp::min(left_h, right_h);
if top > height[mid_pos] {
ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
}
}
}
stack.push(right_pos);
}
ans
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Rust
Two-Pointer
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let n = height.len();
let mut max_left = vec![0; height.len()];
let mut max_right = vec![0; height.len()];
max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
let lmax = lm.max(height[idx]);
let rmax = rm.max(height[n - 1 - idx]);
*x = lmax; *y = rmax;
(lmax, rmax)
});
height.iter().enumerate().fold(0, |acc, (idx, x)| {
let h = max_left[idx].min(max_right[idx]);
if h > 0 { h - x + acc } else { acc }
})
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Monotonic Stack:
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let mut stack = vec![];
let mut ans = 0;
for (right_pos, &right_h) in height.iter().enumerate() {
while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
let mid_pos = stack.pop().unwrap();
if !stack.is_empty() {
let left_pos = *stack.last().unwrap();
let left_h = height[left_pos];
let top = std::cmp::min(left_h, right_h);
if top > height[mid_pos] {
ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
}
}
}
stack.push(right_pos);
}
ans
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
