# 84. Largest Rectangle in Histogram
LeetCode Problem Link (opens new window)
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of the largest rectangle in the histogram.
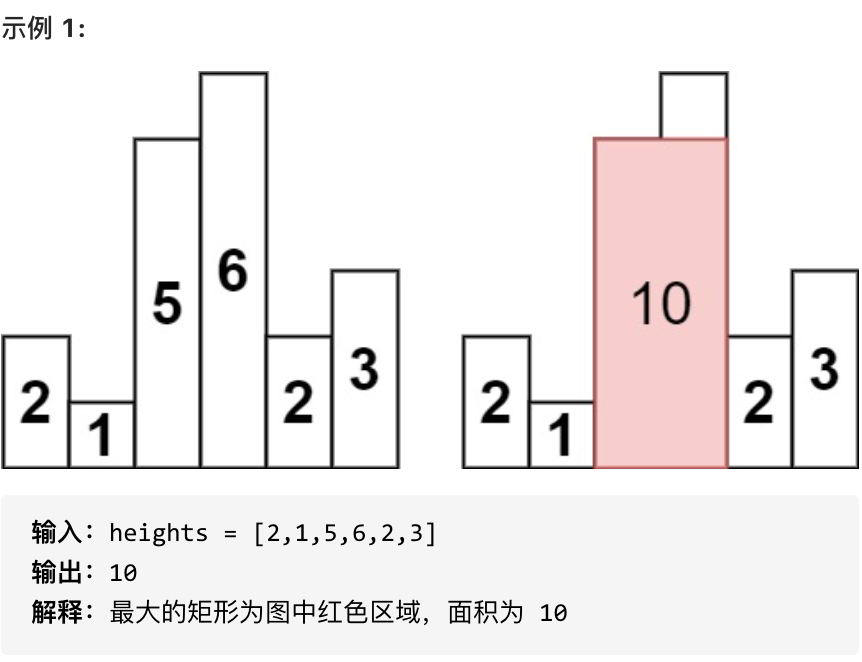
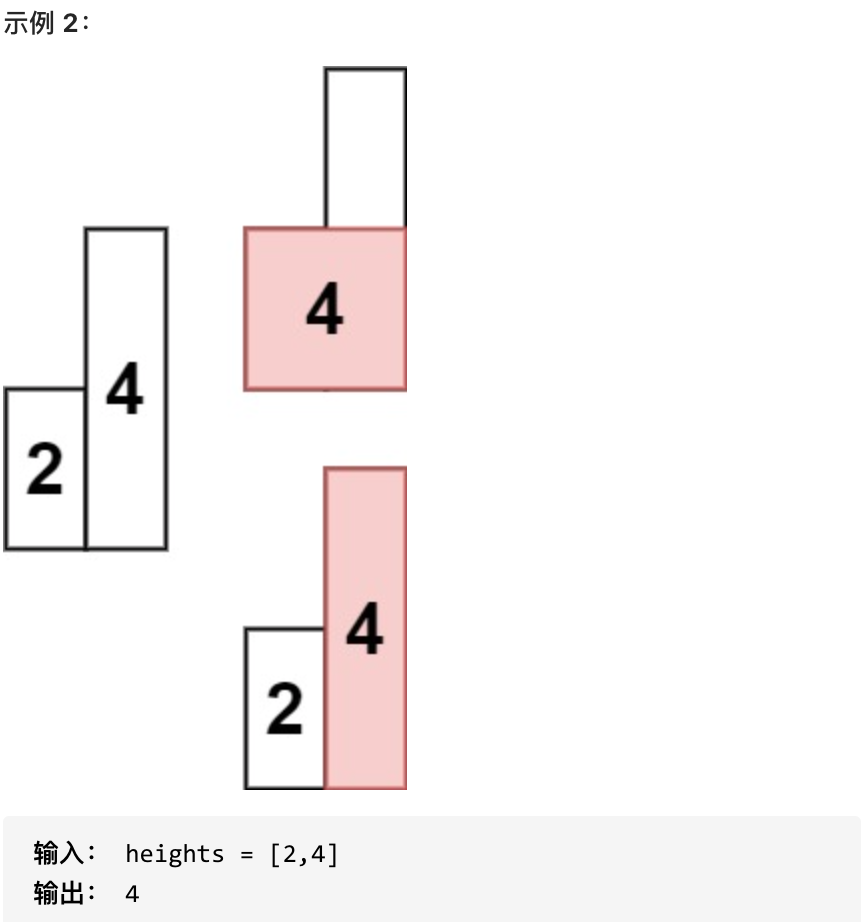
- 1 <= heights.length <= 10^5
- 0 <= heights[i] <= 10^4
# Approach
This problem is closely related to 42. Trapping Rain Water (opens new window), and I suggest trying both problems as they share underlying principles but differ in details, which can enhance your understanding of monotonic stacks.
You can tackle either problem initially; I wrote the explanation for "Trapping Rain Water" first. If you're unfamiliar with it, try solving that problem and reference my 42. Trapping Rain Water (opens new window) explanation.
Let's explore the brute force approach initially:
# Brute Force Approach
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int sum = 0;
for (int i = 0; i < heights.size(); i++) {
int left = i;
int right = i;
for (; left >= 0; left--) {
if (heights[left] < heights[i]) break;
}
for (; right < heights.size(); right++) {
if (heights[right] < heights[i]) break;
}
int w = right - left - 1;
int h = heights[i];
sum = max(sum, w * h);
}
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
The above code cannot pass in LeetCode due to time limit exceeded, as its time complexity is $O(n^2)$.
# Two-pointer Approach
The two-pointer approach for this problem is conceptually similar to that in 42. Trapping Rain Water (opens new window), but it's slightly more challenging.
The additional challenge is that we need to record the first index to the left of each bar where the height is smaller, not just the highest smaller height to the left.
Thus, this requires a looping search, which is reflected in the use of a while loop below. Details are further elaborated in the notes in 42. Trapping Rain Water (opens new window).
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// Record the first index to the left of each bar that is smaller
minLeftIndex[0] = -1; // Initialized to prevent infinite while loop
for (int i = 1; i < size; i++) {
int t = i - 1;
// Not using if, keep searching left until finding the target
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// Record the first index to the right of each bar that is smaller
minRightIndex[size - 1] = size; // Initialized to prevent infinite while loop
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// Keep searching right for the target, not using if
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// Calculate area
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Monotonic Stack
The monotonic stack approach for this problem is conceptually to its counterpart in "Trapping Rain Water".
In 42. Trapping Rain Water (opens new window), you look for the first larger bar to the left and right, while in this problem, you look for the first smaller bar to the left and right.
The core idea here is the sequence inside the mono-stack: whether it's from small to large or from large to small.
In 42. Trapping Rain Water (opens new window), I've explained the monotonic stack sequence, which should be from small to large from the top of the stack (elements popped from the top) to the bottom.
Meanwhile, for this problem, since we are seeking the first smaller bar on both sides of each bar, the sequence should be from large to small from the top of the stack to the bottom!
Let me illustrate with an example:
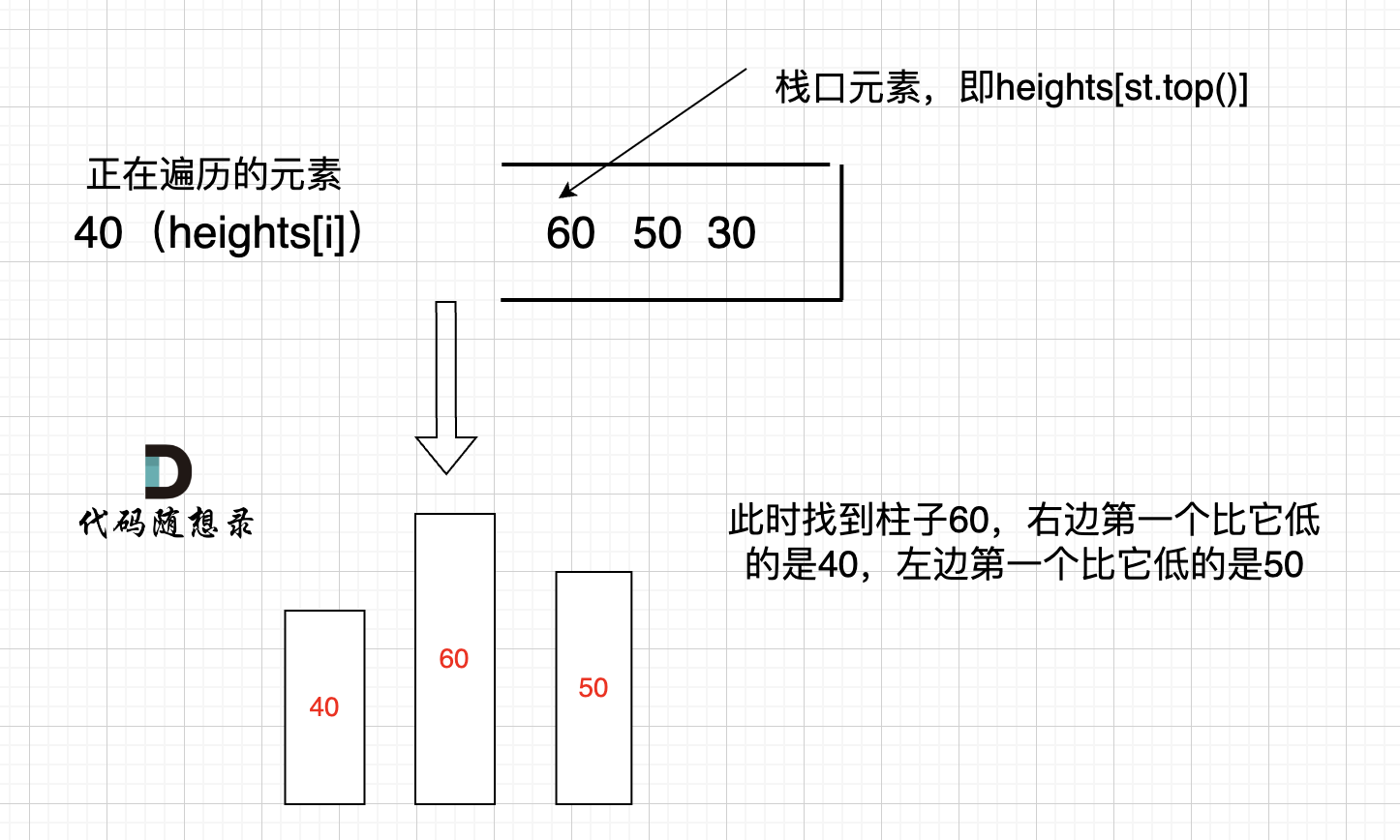
Only by maintaining a sequence from large to small in the stack can it ensure that the stack's top element can find the first smaller bars to its left and right.
Thus, the stack sequence for this problem is precisely reversed compared to "Trapping Rain Water".
Once grasping that it's the three elements—the stack top, the next on the stack, and the incoming element—that form the maximum area height and width, you're on the right path to mastering monotonic stacks.
The logic is virtually identical to that in 42. Trapping Rain Water (opens new window), which I've thoroughly elaborated. Here, I won't repeat that discussion.
Focus primarily on analyzing these three situations:
- Scenario 1: The current element,
heights[i], is greater than the stack top element,heights[st.top()]. - Scenario 2: The current element,
heights[i], equals the stack top element,heights[st.top()]. - Scenario 3: The current element,
heights[i], is smaller than the stack top element,heights[st.top()].
C++ code implementation is as follows:
// Version 1
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int result = 0;
stack<int> st;
heights.insert(heights.begin(), 0); // Insert 0 at the beginning
heights.push_back(0); // Insert 0 at the end
st.push(0);
// First element is already in the stack, start from index 1
for (int i = 1; i < heights.size(); i++) {
if (heights[i] > heights[st.top()]) { // Scenario 1
st.push(i);
} else if (heights[i] == heights[st.top()]) { // Scenario 2
st.pop(); // Can be added or not, same effect, different idea
st.push(i);
} else { // Scenario 3
while (!st.empty() && heights[i] < heights[st.top()]) { // Note, it's while
int mid = st.top();
st.pop();
if (!st.empty()) {
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
}
st.push(i);
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
You might notice that I've added an element 0 at both the head and end of the height array. Why is this necessary?
Let's first discuss why a 0 is added at the end:
If the array is already in an ascending order, like [2,4,6,8], they will all be added to the stack in a monotonic decreasing order without ever hitting Scenario 3 to compute the result, hence finally printing 0. As shown:
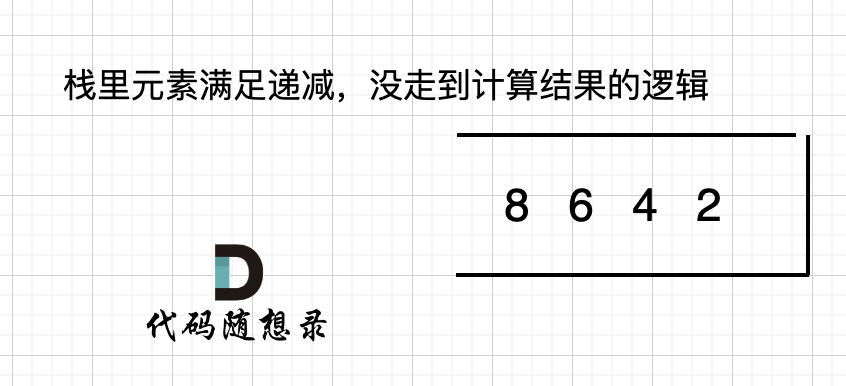
Adding a 0 at the end forces each element in the stack to evaluate Scenario 3.
Why is there a need to add a 0 at the front?
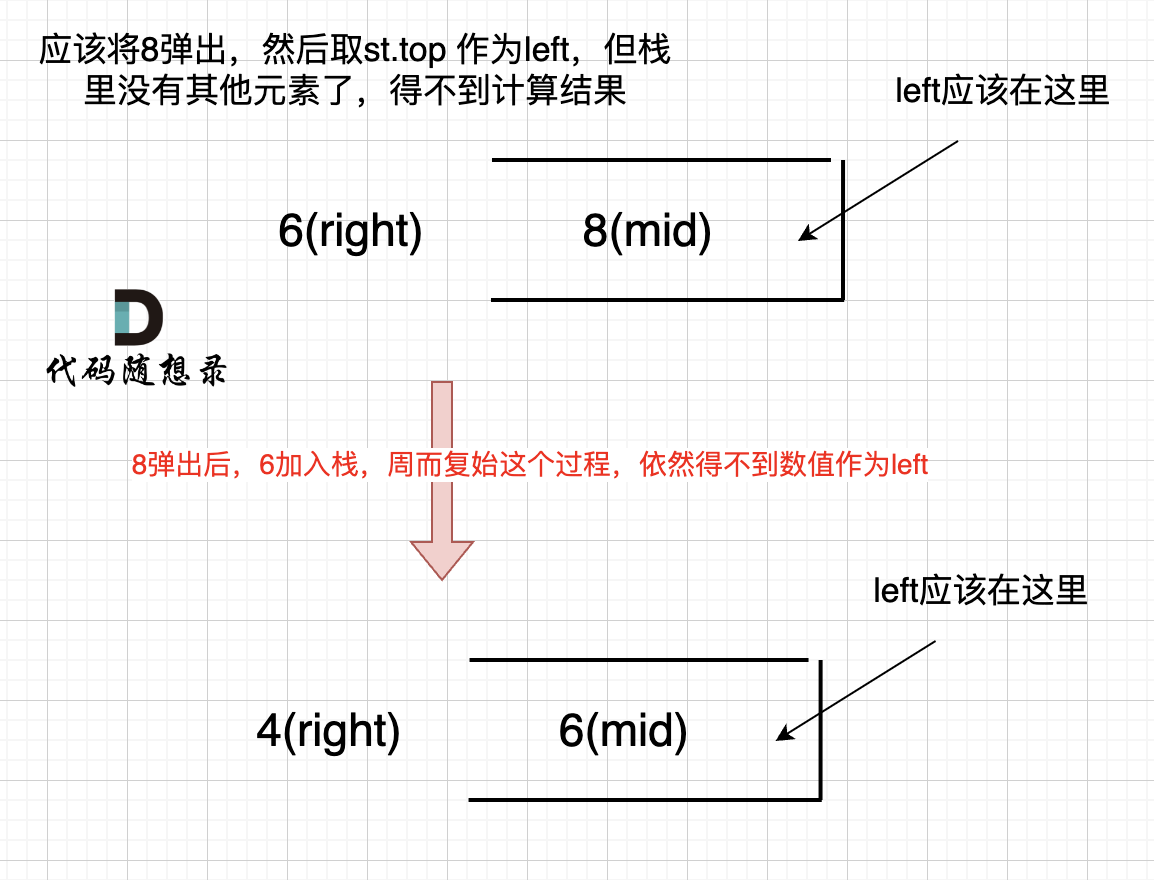
If the array is in descending order, like [8,6,4,2], after 8 is stacked, 6 will start comparing with 8 at the top. At this point, we get mid (8) and right (6), but no left.
Since 8 is popped, the stack becomes empty, skipping the area calculation process. Then 6 is stacked (at which point 8 is already popped), and then it's 4 comparing with top element 6, repeating this process leading the result to only be 0. As shown:
Thus, we should add a 0 at both the start and end of the heights array.
Refined code in version two:
// Version 2
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // Insert 0 at the beginning
heights.push_back(0); // Insert 0 at the end
st.push(0);
int result = 0;
for (int i = 1; i < heights.size(); i++) {
while (heights[i] < heights[st.top()]) {
int mid = st.top();
st.pop();
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
I recommend writing out Version 1 step by step, analyzing Scenarios 1, 2, and 3 carefully, and then refining it to Version 2. Jumping straight to Version 2 may cause you to miss details!
# Other Languages Versions
# Java:
Brute Force:
class Solution {
public int largestRectangleArea(int[] heights) {
int length = heights.length;
int[] minLeftIndex = new int[length];
int[] minRightIndex = new int[length];
// Record the first index to the left of each bar that is smaller
minLeftIndex[0] = -1;
for (int i = 1; i < length; i++) {
int t = i - 1;
// Keep moving left to find the first smaller bar
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// Record the first index to the right of each bar that is smaller
minRightIndex[length - 1] = length;
for (int i = length - 2; i >= 0; i--) {
int t = i + 1;
// Keep moving right to find the first smaller bar
while(t < length && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// Compute the area
int result = 0;
for (int i = 0; i < length; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = Math.max(sum, result);
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Monotonic Stack:
class Solution {
int largestRectangleArea(int[] heights) {
Stack<Integer> st = new Stack<Integer>();
// Expand the array by adding elements at the head and tail
int[] newHeights = new int[heights.length + 2];
newHeights[0] = 0;
newHeights[newHeights.length - 1] = 0;
for (int index = 0; index < heights.length; index++){
newHeights[index + 1] = heights[index];
}
heights = newHeights;
st.push(0);
int result = 0;
// Skip to index 1 since the first element is initialized into the stack
for (int i = 1; i < heights.length; i++) {
// Note that heights[i] is compared to heights[st.peek()], st.peek() is an index
if (heights[i] > heights[st.peek()]) {
st.push(i);
} else if (heights[i] == heights[st.peek()]) {
st.pop(); // This can be added or skipped, resulting in the same outcome with a different perspective
st.push(i);
} else {
while (heights[i] < heights[st.peek()]) { // Notably a while loop
int mid = st.peek();
st.pop();
int left = st.peek();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = Math.max(result, w * h);
}
st.push(i);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Refined Code for Monotonic Stack:
class Solution {
public int largestRectangleArea(int[] heights) {
int[] newHeight = new int[heights.length + 2];
System.arraycopy(heights, 0, newHeight, 1, heights.length);
newHeight[heights.length+1] = 0;
newHeight[0] = 0;
Stack<Integer> stack = new Stack<>();
stack.push(0);
int res = 0;
for (int i = 1; i < newHeight.length; i++) {
while (newHeight[i] < newHeight[stack.peek()]) {
int mid = stack.pop();
int w = i - stack.peek() - 1;
int h = newHeight[mid];
res = Math.max(res, w * h);
}
stack.push(i);
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Python3:
# Brute force approach (times out in leetcode)
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
# Traverse from left to right: use each bar as the focal point (the current highest reference), iterate until finding the first smaller bar on the left and right
res = 0
for i in range(len(heights)):
left = i
right = i
# Find the first smaller bar on the left
for _ in range(left, -1, -1):
if heights[left] < heights[i]:
break
left -= 1
# Find the first smaller bar on the right
for _ in range(right, len(heights)):
if heights[right] < heights[i]:
break
right += 1
width = right - left - 1
height = heights[i]
res = max(res, width * height)
return res
# Two-pointer approach
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
size = len(heights)
# Both DP arrays store indices
min_left_index = [0] * size
min_right_index = [0] * size
result = 0
# Record for each bar the first smaller bar index on the left
min_left_index[0] = -1 # Initialize to prevent while loop from hanging
for i in range(1, size):
# As core shaft, search left for secondary bar
temp = i - 1
while temp >= 0 and heights[temp] >= heights[i]:
# If left bar continues higher, try using that bar's own secondary bar (DP)
temp = min_left_index[temp]
# When a smaller bar is found to the left
min_left_index[i] = temp
# Record the index of the first smaller bar on the right
min_right_index[size-1] = size # Initialization to prevent hanging while loops
for i in range(size-2, -1, -1):
# As core shaft, search right for secondary bar
temp = i + 1
while temp < size and heights[temp] >= heights[i]:
# If right bar continues higher, try using that bar's own secondary bar (DP)
temp = min_right_index[temp]
# When a smaller bar is found to the right
min_right_index[i] = temp
for i in range(size):
area = heights[i] * (min_right_index[i] - min_left_index[i] - 1)
result = max(area, result)
return result
# Monotonic stack
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
# Monotonic Stack
'''
Find the first bar on the left and right whose height is smaller than the given one
Monotonic stack: From stack top to stack bottom: strictly decreasing order (whenever inserting a new smaller value, pop all preceding larger values)
Stack top, the next stack element, and the element ready to be pushed: The trio that forms the maximum area of height and width
Case 1: The current traversed height[i] is greater than the top stack height[st.top()]
Case 2: The current traversed height[i] is equal to the top stack height[st.top()]
Case 3: The current traversed height[i] is less than the top stack height[st.top()]
'''
# Add 0 at both the start and end of the given array. The prime goal here is to automatically compute the areas of the first and the last element.
heights.insert(0, 0)
heights.append(0)
stack = [0]
result = 0
# Start from 1 since the first element is already in the stack
for i in range(1, len(heights)):
# Case 1
if heights[i] > heights[stack[-1]]:
stack.append(i)
# Case 2
elif heights[i] == heights[stack[-1]]:
stack.pop()
stack.append(i)
# Case 3
else:
# Remove all taller bars than heights[i] in the stack
while stack and heights[i] < heights[stack[-1]]:
mid_index = stack[-1]
stack.pop()
if stack:
left_index = stack[-1]
right_index = i
width = right_index - left_index - 1
height = heights[mid_index]
result = max(result, width * height)
stack.append(i)
return result
# Simplified monotonic stack
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
heights.insert(0, 0)
heights.append(0)
stack = [0]
result = 0
for i in range(1, len(heights)):
while stack and heights[i] < heights[stack[-1]]:
mid_height = heights[stack[-1]]
stack.pop()
if stack:
area = (i - stack[-1] - 1) * mid_height
result = max(area, result)
stack.append(i)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
# Go:
Brute Force Approach:
func largestRectangleArea(heights []int) int {
sum := 0
for i := 0; i < len(heights); i++ {
left, right := i, i
for left >= 0 {
if heights[left] < heights[i] {
break
}
left--
}
for right < len(heights) {
if heights[right] < heights[i] {
break
}
right++
}
w := right - left - 1
h := heights[i]
sum = max(sum, w * h)
}
return sum
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Two-pointer Approach:
func largestRectangleArea(heights []int) int {
size := len(heights)
minLeftIndex := make([]int, size)
minRightIndex := make([]int, size)
// Record the first index to the left of each bar that is smaller
minLeftIndex[0] = -1 // Note initialization to avoid infinite loop in while
for i := 1; i < size; i++ {
t := i - 1
// Not just using if, keep finding to the left
for t >= 0 && heights[t] >= heights[i] {
t = minLeftIndex[t]
}
minLeftIndex[i] = t
}
// Record each bar's first smaller bar on the right
minRightIndex[size - 1] = size // Note initialization to avoid infinite while loop
for i := size - 2; i >= 0; i-- {
t := i + 1
// While not if, keep finding to the right
for t < size && heights[t] >= heights[i] {
t = minRightIndex[t]
}
minRightIndex[i] = t
}
// Calculate area
result := 0
for i := 0; i < size; i++ {
sum := heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1)
result = max(sum, result)
}
return result
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Monotonic Stack Approach:
func largestRectangleArea(heights []int) int {
result := 0
heights = append([]int{0}, heights...) // Insert 0 at the start
heights = append(heights, 0) // Insert 0 at the end
st := []int{0}
// First element is already in the stack, start from index 1
for i := 1; i < len(heights); i++ {
if heights[i] > heights[st[len(st)-1]] {
st = append(st, i)
} else if heights[i] == heights[st[len(st)-1]] {
st = st[:len(st)-1]
st = append(st, i)
} else {
for len(st) > 0 && heights[i] < heights[st[len(st)-1]] {
mid := st[len(st)-1]
st = st[:len(st)-1]
if len(st) > 0 {
left := st[len(st)-1]
right := i
w := right - left - 1
h := heights[mid]
result = max(result, w * h)
}
}
st = append(st, i)
}
}
return result
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Simplified Monotonic Stack:
func largestRectangleArea(heights []int) int {
max := 0
// Use slice to implement stack
stack := make([]int, 0)
// Add 0 to the head of the array
heights = append([]int{0}, heights...)
// Add 0 at the end of the array
heights = append(heights, 0)
stack = append(stack, 0)
for i := 1; i < len(heights); i++ {
// End loop when element to be pushed is greater than the top element
for heights[stack[len(stack) - 1]] > heights[i] {
mid := stack[len(stack) - 1]
stack = stack[0 : len(stack) - 1]
left := stack[len(stack) - 1]
tmp := heights[mid] * (i - left - 1)
if tmp > max {
max = tmp
}
}
stack = append(stack, i)
}
return max
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# JavaScript:
// Two-pointer js implementation
var largestRectangleArea = function(heights) {
const len = heights.length;
const minLeftIndex = new Array(len);
const maxRightIndex = new Array(len);
// Record the first index to the left of each bar that is smaller
minLeftIndex[0] = -1;
for(let i = 1; i < len; i++) {
let t = i - 1;
while (t >= 0 && heights[t] >= heights[i]) {
t = minLeftIndex[t];
}
minLeftIndex[i] = t;
}
// Record the first index to the right of each bar that is smaller
maxRightIndex[len - 1] = len;
for(let i = len - 2; i >= 0; i--){
let t = i + 1;
while (t <= n && heights[t] > heights[i]) {
t = maxRightIndex[t];
}
maxRightIndex[i] = t;
}
// Calculate area
let maxArea = 0;
for(let i = 0; i < len; i++){
let sum = heights[i] * (maxRightIndex[i] - minLeftIndex[i] - 1);
maxArea = Math.max(maxArea , sum);
}
return maxArea;
};
// Monotonic stack
var largestRectangleArea = function(heights) {
let maxArea = 0;
const stack = [0];
heights.push(0);
const n = heights.length;
for (let i = 1; i < n; i++) {
let top = stack.at(-1);
if (heights[top] < heights[i]) {
stack.push(i);
}
if (heights[top] === heights[i]) {
stack.pop();
stack.push(i);
}
if (heights[top] > heights[i]) {
while (stack.length > 0 && heights[top] > heights[i]) {
const h = heights[stack.pop()];
const left = stack.at(-1) ?? -1;
const w = i - left - 1;
maxArea = Math.max(maxArea, w * h);
top = stack.at(-1);
}
stack.push(i);
}
}
return maxArea;
};
// Simplified Monotonic stack
var largestRectangleArea = function(heights) {
let maxArea = 0;
const stack = [];
heights = [0,...heights,0];
for(let i = 0; i < heights.length; i++){
while(heights[i] < heights[stack[stack.length-1]]){
const stackTopIndex = stack.pop();
let w = i - stack[stack.length -1] - 1;
let h = heights[stackTopIndex]
maxArea = Math.max(maxArea, w * h);
}
stack.push(i);
}
return maxArea;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
# TypeScript:
Brute Force (will timeout):
function largestRectangleArea(heights: number[]): number {
let resMax: number = 0;
for (let i = 0, length = heights.length; i < length; i++) {
let left: number = i - 1,
right: number = i + 1;
while (left >= 0 && heights[left] >= heights[i]) {
left--;
}
while (right < length && heights[right] >= heights[i]) {
right++;
}
resMax = Math.max(resMax, heights[i] * (right - left - 1));
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Two-pointer preprocessing:
function largestRectangleArea(heights: number[]): number {
const length: number = heights.length;
const leftHeightDp: number[] = [],
rightHeightDp: number[] = [];
leftHeightDp[0] = -1;
rightHeightDp[length - 1] = length;
for (let i = 1; i < length; i++) {
let j = i - 1;
while (j >= 0 && heights[i] <= heights[j]) {
j = leftHeightDp[j];
}
leftHeightDp[i] = j;
}
for (let i = length - 2; i >= 0; i--) {
let j = i + 1;
while (j < length && heights[i] <= heights[j]) {
j = rightHeightDp[j];
}
rightHeightDp[i] = j;
}
let resMax: number = 0;
for (let i = 0; i < length; i++) {
let area = heights[i] * (rightHeightDp[i] - leftHeightDp[i] - 1);
resMax = Math.max(resMax, area);
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Monotonic Stack:
function largestRectangleArea(heights: number[]): number {
heights.push(0);
const length: number = heights.length;
const stack: number[] = [];
stack.push(0);
let resMax: number = 0;
for (let i = 1; i < length; i++) {
let top = stack[stack.length - 1];
if (heights[top] < heights[i]) {
stack.push(i);
} else if (heights[top] === heights[i]) {
stack.pop();
stack.push(i);
} else {
while (stack.length > 0 && heights[top] > heights[i]) {
let mid = stack.pop();
let left = stack.length > 0 ? stack[stack.length - 1] : -1;
let w = i - left - 1;
let h = heights[mid];
resMax = Math.max(resMax, w * h);
top = stack[stack.length - 1];
}
stack.push(i);
}
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Rust:
Two-pointer preprocessing
impl Solution {
pub fn largest_rectangle_area(v: Vec<i32>) -> i32 {
let n = v.len();
let mut left_smaller_idx = vec![-1; n];
let mut right_smaller_idx = vec![n as i32; n];
for i in 1..n {
let mut mid = i as i32 - 1;
while mid >= 0 && v[mid as usize] >= v[i] {
mid = left_smaller_idx[mid as usize];
}
left_smaller_idx[i] = mid;
}
for i in (0..n-1).rev() {
let mut mid = i + 1;
while mid < n && v[mid] >= v[i] {
mid = right_smaller_idx[mid] as usize;
}
right_smaller_idx[i] = mid as i32;
}
let mut res = 0;
for (idx, &e) in v.iter().enumerate() {
res = res.max((right_smaller_idx[idx] - left_smaller_idx[idx] - 1) * e);
}
dbg!(res)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Monotonic stack
impl Solution {
pub fn largest_rectangle_area1(mut v: Vec<i32>) -> i32 {
v.insert(0, 0); // Facilitate processing the first element with comparable smaller values on the left
v.push(0); // Facilitate clearing remaining values in the stack post processing of the last element
let mut res = 0;
let mut stack = vec![]; // Decreasing stack
for (idx, &e) in v.iter().enumerate() {
while !stack.is_empty() && v[*stack.last().unwrap()] > e {
let pos = stack.pop().unwrap();
let prev_pos = *stack.last().unwrap();
let s = (idx - prev_pos - 1) as i32 * v[pos];
res = res.max(s);
}
stack.push(idx);
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
