KMP algorithm can even do this

459. Repeated Substring Pattern

LeetCode Problem Link (opens new window)

Given a non-empty string, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together. The given string contains only lowercase English letters and has a length not exceeding 10000.

Example 1:

• Input: "abab"
• Output: True
• Explanation: It can be constructed by repeating the substring "ab" twice.

Example 2:

• Input: "aba"
• Output: False

Example 3:

• Input: "abcabcabcabc"
• Output: True
• Explanation: It can be constructed by repeating the substring "abc" four times. (Or the substring "abcabc" twice.)

Approach

A brute force solution involves using a for loop to get the endpoint of the substring and then checking whether the substring can be repeated to form the string, involving an inner for loop, making the time complexity O(n^2).

Some might think they need two loops: one for the starting point and one for the ending point of the substring. However, you only need to check substrings starting at the first character, so a single for loop to get the endpoint suffices. Moreover, you don't need to loop through the entire string; checking up to the midpoint is enough because ending the substring beyond the midpoint cannot form the original string through repetition.

Thus, the brute force method is left unexplored here.

Let's focus on the shifting match and the KMP approach.

Shifting Match

If a string s, e.g., "abcabc", is composed of repeating substrings, it structurally looks like this:

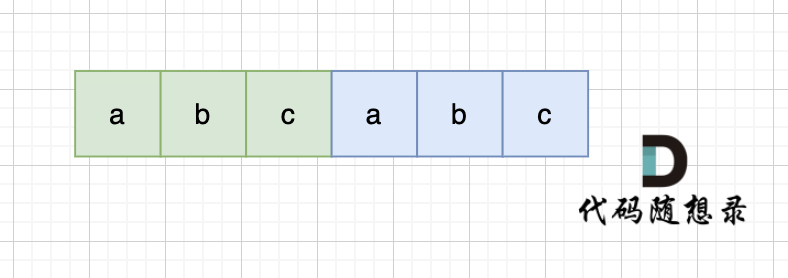
Such a string s has equal-length prefixes and suffixes. Thus, if you concatenate s + s, the string will have overlapping prefix and suffix, forming s again, illustrated as follows:

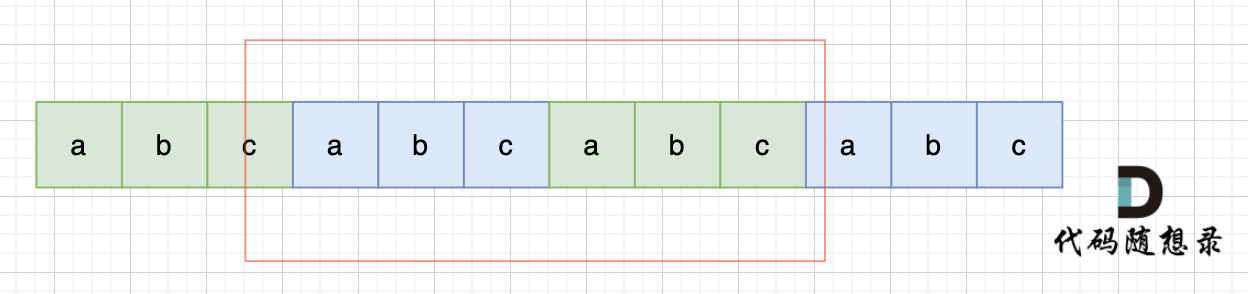
When checking for s in the concatenated string s + s, avoid its very first and last characters to prevent finding the original s; we seek the newly formed s.

The sufficient condition has been shown above; now prove the necessity:

Suppose a string s, upon concatenating to form s + s, can create s in between (excluding its first and last characters); then, s must consist of repeating substrings.

For example, in s with indices depicted, forming s in s + s skipping head and tail characters reveals:

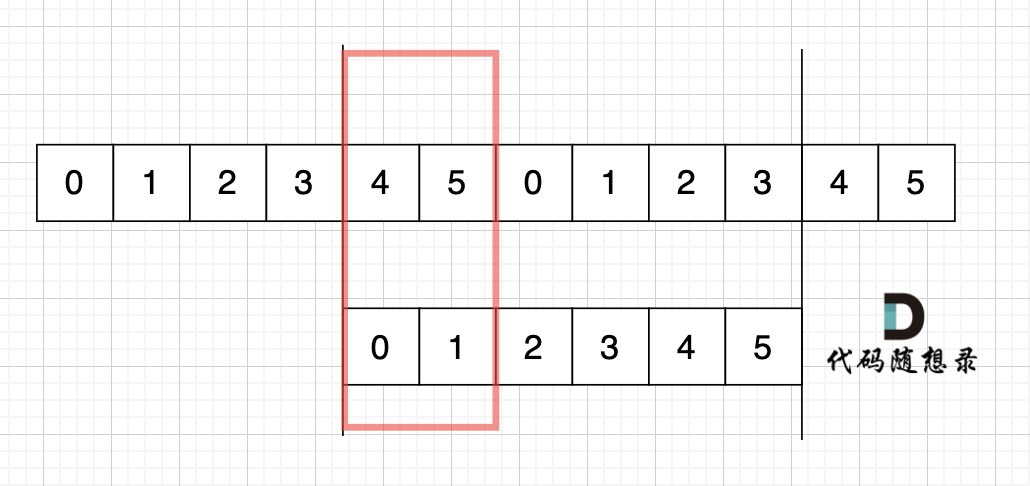
Connecting these equality expressions illustrates:

s[4] = s[0] = s[2]
s[5] = s[1] = s[3]

Thus, s[4], s[5] = s[0], s[1] = s[2], s[3], implying that the string comprises repeating characters: s[0] and s[1].

However, if the structure had been different, with the same connecting equality . . ., it proves to be a single character repetition like aaaaaa.

Hence, it’s concluded: verifying s can be formed by another s in s + s confirms repetitive substrings.

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string t = s + s;
        t.erase(t.begin()); t.erase(t.end() - 1); // remove head and tail
        return t.find(s) != std::string::npos; //
    }
};

• Time Complexity: O(n)
• Space Complexity: O(1)

A side note: finding a string within another, even through library functions like contains or find, might obscure algorithmic complexity (naïve is m * n, libraries typically O(m + n)). The high efficiency of such implementations often leans on KMP.

KMP

Why Use KMP?

Having the ability to efficiently search string occurrences is KMP's strength. How does it relate to finding repeated substrings?

KMP's next array allows characters to re-match upon mismatch through precomputed prefix tables. These tables correlate directly with longest matching prefix and suffix.

But how do these play a part in repeated substrings?

A recollection on prefix/suffix definitions:

• A prefix is any consecutive string starting at the first character, excluding the final one.
• A suffix is any consecutive string ending at the last character, excluding the first one.

Sufficiency Proof

If a string s consists of repeating substrings, the longest corresponding prefix not overlapped by suffix forms the smallest repeating substring pattern for s. Thus, if s = n * p, regarding the overlapping prefix-suffix shows:

Any longer conceivable prefix would indicate a more fundamental repeating substring p, thus evident in s = p1 * 3, where p = p1 == p2 == ....

Hence, breaking s into smallest repeating units leads the longest non-overlapping prefix-suffix as s.

Necessity Proof

Again, suppose this prefix-suffix makes ss, indicating repetitions. When does this emerge as the smallest repeatable segment --

Scenario 1: Longer non-overlapping is already half string length or more, ineligible for repeated segments.

Scenario 2: The length divisible by s; repeat patterns surface, revealing smallest repeated patterns.

Scenario 3: Failure to divide s into its smallest segment shows a repeat.

Code Analysis

The KMP method next array represents the length of longest matching prefix and suffix. If next[len - 1] != -1, longest prefix exists. Its length next[len - 1] + 1. Length of s divides len - (next[len - 1] + 1) which implies repeat patterns.

class Solution {
public:
    void getNext (int* next, const string& s){
        next[0] = -1;
        int j = -1;
        for(int i = 1;i < s.size(); i++){
            while(j >= 0 && s[i] != s[j + 1]) {
                j = next[j];
            }
            if(s[i] == s[j + 1]) {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) {
            return true;
        }
        return false;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

C++ (alternative without decrement in prefix table):

class Solution {
public:
    void getNext (int* next, const string& s){
        next[0] = 0;
        int j = 0;
        for(int i = 1;i < s.size(); i++){
            while(j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if(s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

Other Language Versions

Java:

// Version 1: Using prefix table with decrement
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        if (s.equals("")) return false;
        int len = s.length();
        s = " " + s;
        char[] chars = s.toCharArray();
        int[] next = new int[len + 1];
        for (int i = 2, j = 0; i <= len; i++) {
            while (j > 0 && chars[i] != chars[j + 1]) j = next[j];
            if (chars[i] == chars[j + 1]) j++;
            next[i] = j;
        }
        if (next[len] > 0 && len % (len - next[len]) == 0) {
            return true;
        }
        return false;
    }
}

// Version 2: Using prefix table without decrement
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int n = s.length();
        int[] next = new int[n];
        int j = 0;
        next[0] = 0;
        for (int i = 1; i < n; i++) {
            while (j > 0 && s.charAt(i) != s.charAt(j)) {
                j = next[j - 1];
            }
            if (s.charAt(i) == s.charAt(j)) {
                j++;
            }
            next[i] = j;
        }
        if (next[n - 1] > 0 && n % (n - next[n - 1]) == 0) {
            return true;
        } else {
            return false;
        }
    }
}

Python:

# Version 1: Prefix table with decrement
class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:  
        if len(s) == 0:
            return False
        nxt = [0] * len(s)
        self.getNext(nxt, s)
        if nxt[-1] != -1 and len(s) % (len(s) - (nxt[-1] + 1)) == 0:
            return True
        return False
    
    def getNext(self, nxt, s):
        nxt[0] = -1
        j = -1
        for i in range(1, len(s)):
            while j >= 0 and s[i] != s[j+1]:
                j = nxt[j]
            if s[i] == s[j+1]:
                j += 1
            nxt[i] = j
        return nxt

# Version 2: Prefix table without decrement
class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:  
        if len(s) == 0:
            return False
        nxt = [0] * len(s)
        self.getNext(nxt, s)
        if nxt[-1] != 0 and len(s) % (len(s) - nxt[-1]) == 0:
            return True
        return False
    
    def getNext(self, nxt, s):
        nxt[0] = 0
        j = 0
        for i in range(1, len(s)):
            while j > 0 and s[i] != s[j]:
                j = nxt[j - 1]
            if s[i] == s[j]:
                j += 1
            nxt[i] = j
        return nxt

# Version 3: Using find
class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:
        n = len(s)
        if n <= 1:
            return False
        ss = s[1:] + s[:-1] 
        print(ss.find(s))              
        return ss.find(s) != -1

# Version 4: Brute force
class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:
        n = len(s)
        if n <= 1:
            return False
        
        substr = ""
        for i in range(1, n//2 + 1):
            if n % i == 0:
                substr = s[:i]
                if substr * (n//i) == s:
                    return True
                
        return False

Go:

func repeatedSubstringPattern(s string) bool {
	n := len(s)
	if n == 0 {
		return false
	}
	j := 0
	next := make([]int, n)
	next[0] = j
	for i := 1; i < n; i++ {
		for j > 0 && s[i] != s[j] {
			j = next[j-1]
		}
		if s[i] == s[j] {
			j++
		}
		next[i] = j
	}
	if next[n-1] != 0 && n%(n-next[n-1]) == 0 {
		return true
	}
	return false
}

// Shifting match
func repeatedSubstringPattern(s string) bool {
    if len(s) == 0 {
        return false
    }
    t := s + s
    return strings.Contains(t[1:len(t)-1], s)
}

JavaScript:

// Prefix table with decrement
var repeatedSubstringPattern = function (s) {
    if (s.length === 0)
        return false;

    const getNext = (s) => {
        let next = [];
        let j = -1;

        next.push(j);

        for (let i = 1; i < s.length; ++i) {
            while (j >= 0 && s[i] !== s[j + 1])
                j = next[j];
            if (s[i] === s[j + 1])
                j++;
            next.push(j);
        }

        return next;
    }

    let next = getNext(s);

    if (next[next.length - 1] !== -1 && s.length % (s.length - (next[next.length - 1] + 1)) === 0)
        return true;
    return false;
};

// Prefix table without decrement
var repeatedSubstringPattern = function (s) {
    if (s.length === 0)
        return false;

    const getNext = (s) => {
        let next = [];
        let j = 0;

        next.push(j);

        for (let i = 1; i < s.length; ++i) {
            while (j > 0 && s[i] !== s[j])
                j = next[j - 1];
            if (s[i] === s[j])
                j++;
            next.push(j);
        }

        return next;
    }

    let next = getNext(s);

    if (next[next.length - 1] !== 0 && s.length % (s.length - next[next.length - 1]) === 0)
        return true;
    return false;
};

// Regex match
var repeatedSubstringPattern = function(s) {
  let reg = /^(\w+)\1+$/
  return reg.test(s)
};

// Shifting match
var repeatedSubstringPattern = function (s) {
    let ss = s + s;
    return ss.substring(1, ss.length - 1).includes(s);
};

TypeScript:

// Prefix table with decrement
function repeatedSubstringPattern(s: string): boolean {
    function getNext(str: string): number[] {
        let next: number[] = [];
        let j: number = -1;
        next[0] = j;
        for (let i = 1; i < str.length; i++) {
            while (j >= 0 && str[i] !== str[j + 1]) {
                j = next[j];
            }
            if (str[i] === str[j + 1]) {
                j += 1;
            }
            next[i] = j;
        }
        return next;
    }

    let next: number[] = getNext(s);
    let sLength: number = s.length;
    let nextLength: number = next.length;
    let suffixLength: number = next[nextLength - 1] + 1;
    if (suffixLength > 0 && sLength % (sLength - suffixLength) === 0) return true;
    return false;
};

// Prefix table without decrement
function repeatedSubstringPattern(s: string): boolean {
    function getNext(str: string): number[] {
        let next: number[] = [];
        let j: number = 0;
        next[0] = j;
        for (let i = 1; i < str.length; i++) {
            while (j > 0 && str[i] !== str[j]) {
                j = next[j - 1];
            }
            if (str[i] === str[j]) {
                j += 1;
            }
            next[i] = j;
        }
        return next;
    }

    let next: number[] = getNext(s);
    let sLength: number = s.length;
    let nextLength: number = next.length;
    let suffixLength: number = next[nextLength - 1];
    if (suffixLength > 0 && sLength % (sLength - suffixLength) === 0) return true;
    return false;
};

Swift:

// Prefix table with decrement
	func repeatedSubstringPattern(_ s: String) -> Bool {
        
        let sArr = Array(s)
        let len = s.count
        if len == 0 {
            return false
        }
        var next = Array.init(repeating: -1, count: len)
        
        getNext(&next,sArr)
        
        if next.last != -1 && len % (len - (next[len-1] + 1)) == 0{
            return true
        }

        return false
    }
    
    func getNext(_ next: inout [Int], _ str:[Character]) {
        
        var j = -1
        next[0] = j
        
        for i in 1 ..< str.count {
            
            while j >= 0 && str[j+1] != str[i] {
                j = next[j]
            }
            
            if str[i] == str[j+1] {
                j += 1
            }
            
            next[i] = j
        }
    }

// Prefix table without decrement
	func repeatedSubstringPattern(_ s: String) -> Bool {
        
        let sArr = Array(s)
        let len = sArr.count
        if len == 0 {
            return false
        }
        
        var next = Array.init(repeating: 0, count: len)
        getNext(&next, sArr)
        
        if next[len-1] != 0 && len % (len - next[len-1]) == 0 {
            return true
        }
        
        return false
    }
    
    // When not decrementing prefix table
    func getNext(_ next: inout [Int], _ sArr:[Character]) {
        
        var j = 0
        next[0] = 0
        
        for  i  in 1 ..< sArr.count {
            
            while j > 0 && sArr[i] != sArr[j] {
                j = next[j-1]
            }
            
            if sArr[i] == sArr[j] {
                j += 1
            }
            
            next[i] = j
        }
    }

Rust:

// Prefix table without decrement
impl Solution {
    pub fn get_next(next: &mut Vec<usize>, s: &Vec<char>) {
        let len = s.len();
        let mut j = 0;
        for i in 1..len {
            while j > 0 && s[i] != s[j] {
                j = next[j - 1];
            }
            if s[i] == s[j] {
                j += 1;
            }
            next[i] = j;
        }
    }

    pub fn repeated_substring_pattern(s: String) -> bool {
        let s = s.chars().collect::<Vec<char>>();
        let len = s.len();
        if len == 0 { return false; };
        let mut next = vec![0; len];
        Self::get_next(&mut next, &s);
        if next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0 { return true; }
        return false;
    }
}

// Prefix table with decrement
impl Solution {
    pub fn get_next(next_len: usize, s: &Vec<char>) -> Vec<i32> {
        let mut next = vec![-1; next_len];
        let mut j = -1;
        for i in 1..s.len() {
            while j >= 0 && s[i] != s[(j + 1) as usize] {
                j = next[j as usize];
            }
            if s[i] == s[(j + 1) as usize] {
                j += 1;
            }
            next[i] = j;
        }
        next
    }
    pub fn repeated_substring_pattern(s: String) -> bool {
        let s_chars = s.chars().collect::<Vec<char>>();
        let next = Self::get_next(s_chars.len(), &s_chars);
        if next[s_chars.len() - 1] >= 0
            && s_chars.len() % (s_chars.len() - (next[s_chars.len() - 1] + 1) as usize) == 0
        {
            return true;
        }
        false
    }
}

C#

// Prefix table without decrement
public bool RepeatedSubstringPattern(string s)
{
    if (s.Length == 0)
        return false;
    int[] next = GetNext(s);
    int len = s.Length;
    if (next[len - 1] != 0 && len % (len - next[len - 1]) == 0) return true;
    return false;
}
public int[] GetNext(string s)
{
    int[] next = Enumerable.Repeat(0, s.Length).ToArray();
    for (int i = 1, j = 0; i < s.Length; i++)
    {
        while (j > 0 && s[i] != s[j])
            j = next[j - 1];
        if (s[i] == s[j])
            j++;
        next[i] = j;
    }
    return next;
}

// Shifting match
public bool RepeatedSubstringPattern(string s) {
    string  ss = (s + s).Substring(1, (s + s).Length - 2);
    return ss.Contains(s);
}

C

// Prefix table without decrement
int *build_next(char* s, int len) {

    int *next = (int *)malloc(len * sizeof(int));
    assert(next);

    next[0] = 0;

    int i = 1, j = 0;
    while (i < len) {
        if (s[i] == s[j]) {
            j++;
            next[i] = j;
            i++;
        } else if (j > 0) {
            j = next[j - 1];
        } else {
            next[i] = 0;
            i++;
        }
    }
    return next;
}

bool repeatedSubstringPattern(char* s) {

    int len = strlen(s);
    int *next = build_next(s, len);
    bool result = false;

    if (next[len - 1]) {
        result = len % (len - next[len - 1]) == 0;
    }

    free(next);
    return result;
}