In a string, find if another string appears in it. This is what the KMP algorithm is known for.
# 28. Implement strStr()
LeetCode Problem Link (opens new window)
Implement the strStr() function.
Given a haystack string and a needle string, find the first occurrence of the needle in the haystack (starting from index 0). If it does not exist, return -1.
Example 1: Input: haystack = "hello", needle = "ll" Output: 2
Example 2: Input: haystack = "aaaaa", needle = "bba" Output: -1
Note: What should we return when needle is an empty string? This is a good question to ask in an interview. For this question, we should return 0 when needle is an empty string. This is consistent with the definition of C’s strstr() and Java’s indexOf() functions.
# Algorithm Open Lecture
This problem is a classic KMP problem. If you find the following text hard to comprehend, you can watch the Algo Lab open lecture video (opens new window). Coupling the video with this explanation may help deepen your understanding of the problem.
- Understand the KMP Algorithm Thoroughly: Bilibili (Theory) (opens new window)
- Understand the KMP Algorithm Thoroughly: Bilibili (Code for next array) (opens new window)
# Approach
The classical idea behind KMP is: When a mismatch happens in the string, it records part of the text that was already matched and uses this information to avoid matching from the start again.
We will explain KMP in the following order:
- What is KMP
- What does KMP do
- What is the prefix table
- Why use the prefix table
- How to calculate the prefix table
- The prefix table and the next array
- Use the next array for matching
- Time complexity analysis
- Constructing the next array
- Using the next array for matching
- C++ implementation with the prefix table subtracting one
- C++ implementation without subtracting one from the prefix table
- Summary
After reading this article, you should be able to tackle LeetCode's Problem 28: Implement strStr().
# What is KMP
The name KMP originated from the inventors: Knuth, Morris, and Pratt, abbreviating the initial letters of their last names. Hence, it’s called KMP.
# What does KMP do
KMP is primarily used for string matching.
Its core idea is utilizing previously matched information to avoid redundant re-matching when an unmatched character is encountered.
The core of KMP is how to store the previously matched part, which is the responsibility of the next array.
Many developers memorize the KMP template code without fully grasping the concept. However, memorizing without understanding, one might stumble if asked about the purpose of each component, such as what the numbers in the next array represent and why?
In the following content, I will help you understand the essence of KMP, especially the next array.
# What is the prefix table
For those who have implemented KMP, you must have written the next array. But what exactly is this next array?
The next array is essentially a prefix table.
What is the purpose of the prefix table?
The prefix table is utilized for backtracking, which records where the pattern string should restart from when a mismatch occurs with the main string.
To understand the derivation of the prefix table, consider the following example:
We need to check whether the pattern string "aabaaf" appears in the text string "aabaabaafa".
Remembering the roles of the text string and the pattern string is crucial. Otherwise, it’s easy to become confused. So, I repeat thrice:
We need to check whether the pattern string "aabaaf" appears in the text string "aabaabaafa".
As shown in the animation:
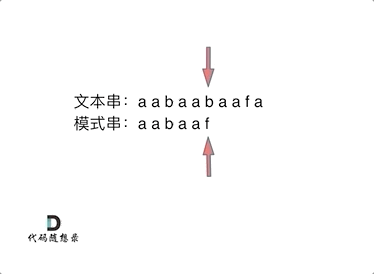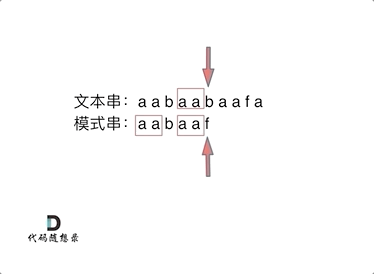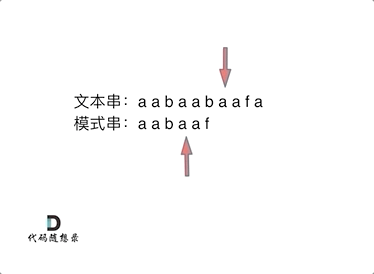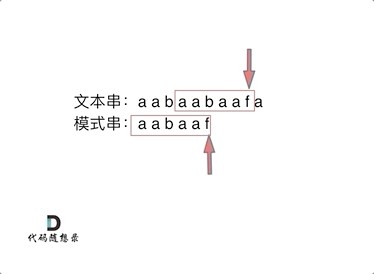
In the animation, I deliberately marked the substring aa. This is intentional; take note, as it will be explained later.
Observing the text string, at the sixth character 'b' and the pattern string's sixth character 'f', they do not match. In a brute force approach, a mismatch would require a restart from the beginning.
However, using the prefix table avoids starting from the beginning, jumping to the third character 'b' in the pattern string to start matching again.
How then is the prefix table recorded?
Primarily, the prefix table's task is that when a current character mismatches, it directs us, based on previously matched positions, to a new point to resume matching.
# Longest Common Prefix and Suffix
The prefix of a string is defined as all continuous substrings beginning with the first character, not including the last character.
The suffix is defined as all continuous substrings ending with the last character, not including the first character.
Understanding what constitutes a prefix and what constitutes a suffix is crucial.
As for the term "Longest Common Prefix and Suffix" frequently appearing in KMP discussions, it's essential to mention that neither "The Algorithm Design Manual" nor "Algorithms, Part I" mentions this term. I believe using "Longest Equal Prefix and Suffix" is more accurate.
Because what the prefix table demands is the length of identical prefixes and suffixes.
Hence for string "a", the longest equal prefix and suffix is 0. For string "aa", it's 1. For string "aaa", it's 2. And so forth....
# Why use the prefix table
This is the prefix table's essence: indicating where a match should be restarted after a mismatch.
Revisiting the matching process, when a mismatch occurs at index 5, the pattern string points to 'f,' as shown:
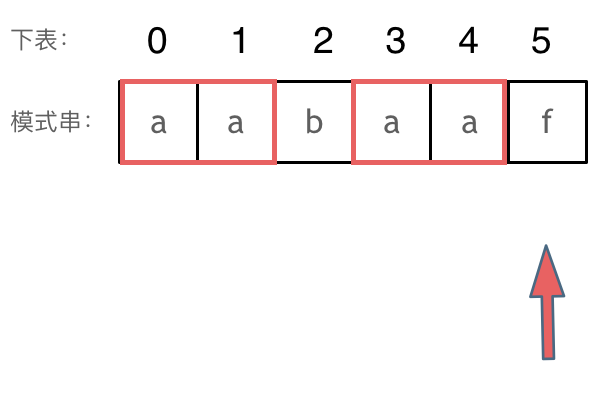
Then, it resumes matching starting from index 2, pointing to 'b,' as shown:
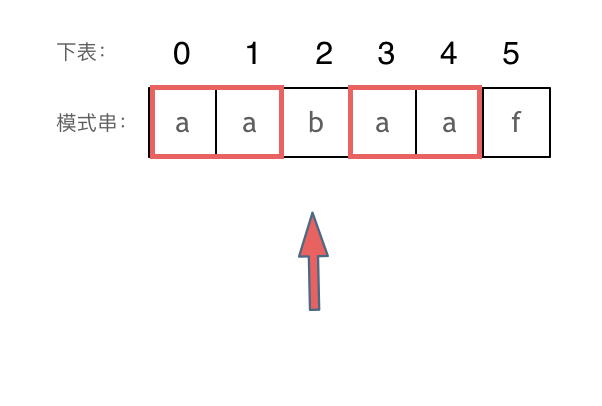
The following sentence is crucial for understanding why the prefix table indicates where to restart matching after a mismatch:
The longest equal prefix and suffix of the string (which is aa) before the mismatch at index 5, directs us to the corresponding prefix of the same length to resume matching.
So, the prefix table effectively informs us where to resume matching after a mismatch occurs.
Many articles or videos introducing KMP do not clarify "Why use the prefix table?" and instead, one assumes its usage without explanation.
# How to calculate the prefix table
Next, let's talk about how to calculate the prefix table.
As shown:
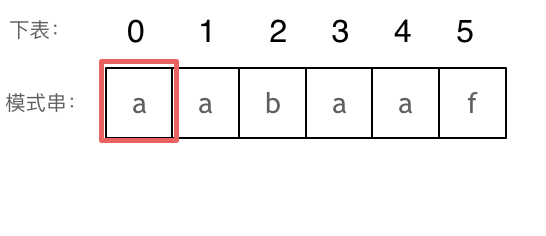
The substring comprising the first 1 character, 'a', has a longest equal prefix and suffix length of 0. The substring comprising the first 2 characters, 'aa', has a longest equal prefix and suffix length of 1.
As shown:
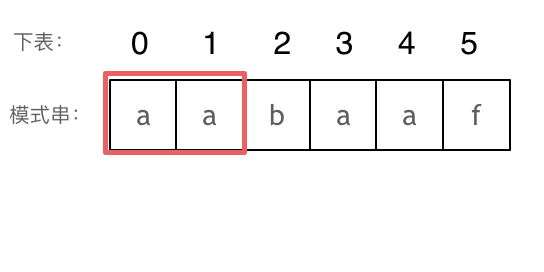
The substring comprising the first 3 characters, 'aab', has a longest equal prefix and suffix length of 0.
And continuing: The substring comprising the first 4 characters, 'aaba', has a longest equal prefix and suffix length of 1. The substring comprising the first 5 characters, 'aabaa', has a longest equal prefix and suffix length of 2. The substring comprising the first 6 characters, 'aabaaf', has a longest equal prefix and suffix length of 0.
Following this, the longest equal prefix and suffix lengths are computed, corresponding to the prefix table's elements, as shown:
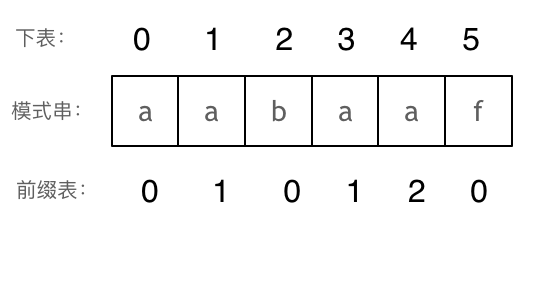
It can be seen that the digits in the prefix table correspond to: the length of the longest equal prefix and suffix for the string prior to index i (including i).
Now let's look at how, using the prefix table, to determine where to move the pointer when a character mismatches. As shown in the animation:
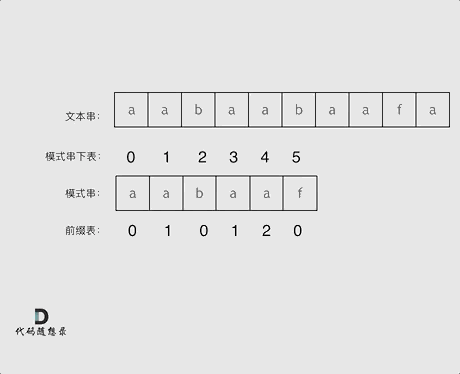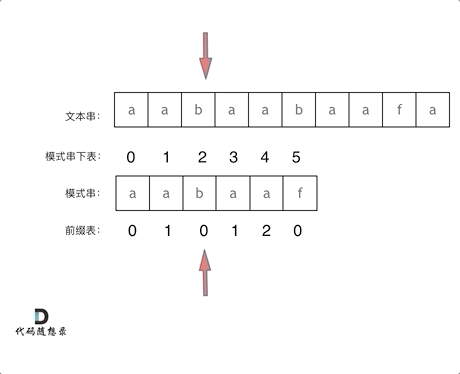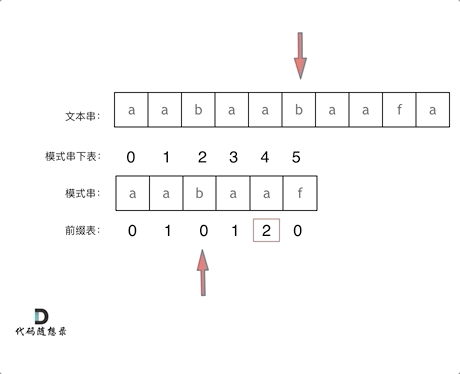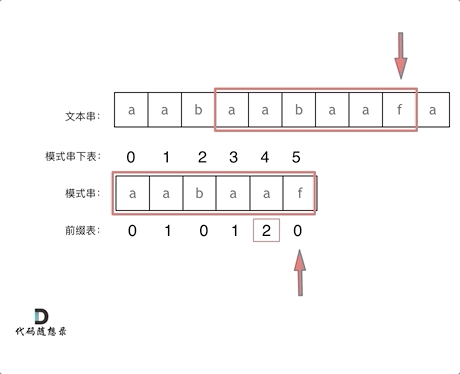
# The prefix table and the next array
Many KMP implementations use the next array for backtracking. So, how is the next array related to the prefix table?
The next array can be the prefix table, but many implementations offset the prefix table by one (right-shift all values, setting the initial value to -1). This acts as the next array.
Why do they do this? This aspect is often unexplained in articles or videos.
Actually, it doesn’t concern the KMP’s principles but its concrete implementation. The next array can either be the prefix table or be a prefix table offset by one.
Later on, I will offer two different implementation codes, and you will understand.
# Use the next array for matching
Below, we use the next array after subtracting one from the prefix table.
With the next array on hand, we can match the text string s with the pattern string t.
Define two pointers, j pointing to the start of the pattern and i pointing to the start of the text.
Therefore, j's initial value remains -1. Why? Because the next array records an initial position of -1.
i starts at 0 to iterate through the text string, as follows:
for (int i = 0; i < s.size(); i++)
Then, compare s[i] with t[j + 1] (note j starts at -1).
If s[i] does not match t[j + 1], then j should point to the next part in the pattern string for matching.
Here’s the code:
while (j >= 0 && s[i] != t[j + 1]) {
j = next[j];
}
2
3
If s[i] matches t[j + 1], both i and j move to the next index:
if (s[i] == t[j + 1]) {
j++;
}
2
3
How can it be determined that string t completely matches a substring in s? It occurs when j points to the end of the pattern string.
In this problem, we need the first occurrence of needle in haystack. Therefore, return the matching position i in the text, then subtract the length of the pattern to get the first position where the substring matches.
The code looks like this:
if (j == (t.size() - 1)) {
return (i - t.size() + 1);
}
2
3
Now, using the next array to find the pattern string t in the text string s, the complete code is as follows:
# C++ Code Implementation with the Prefix Table Subtracting One
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if (s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
vector<int> next(needle.size());
getNext(&next[0], needle);
int j = -1;
for (int i = 0; i < haystack.size(); i++) {
while(j >= 0 && haystack[i] != needle[j + 1]) {
j = next[j];
}
if (haystack[i] == needle[j + 1]) {
j++;
}
if (j == (needle.size() - 1)) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
- Time Complexity: O(n + m)
- Space Complexity: O(m), only need to store the prefix table for string
needle.
# C++ Implementation without Subtracting One from the Prefix Table
Can we use the prefix table directly without subtracting one?
Yes!
As mentioned earlier, it's simply an implementation choice in KMP. We can adjust the backtracking method by setting j=next[j-1].
Our getNext implementation with subtracted prefix table was:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if (s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
Now, here’s the implementation without subtracting one from the prefix table:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
If the input pattern is "aabaaf", the corresponding next values would be 0 1 0 1 2 0, which mirror the prefix table's values.
Utilizing this next array for matching requires slight modifications.
Here is a complete implementation:
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
vector<int> next(needle.size());
getNext(&next[0], needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size()) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
- Time Complexity: O(n + m)
- Space Complexity: O(m)
# Summary
We have discussed what KMP is and what problems KMP can solve. We delved into the next array in KMP, realizing it’s essentially a prefix table. Then, we examined why the prefix table is essential instead of any other method.
Following this, starting from the given pattern string, we derived the prefix table step by step and concluded that using a shifted or unshifted prefix table in KMP ultimately boils down to different implementation choices.
We also analyzed the time complexity of KMP, contrasting it with the brute force method.
Initially, with the shifted prefix table, we matched the pattern in the text. Finally, I furnished implementations of using a non-subtracted prefix table for pattern matching.
In conclusion, we've dissected every minute detail of the KMP algorithm, transparently unveiling it to you!
# Other Language Versions
# Java:
class Solution {
/**
Sacrifice space for direct brute force
Time Complexity: O(n * m)
Space Complexity O(n + m)
*/
public int strStr(String haystack, String needle) {
// Get the length of haystack and needle
int n = haystack.length(), m = needle.length();
// Convert string to character arrays for index operations
char[] s = haystack.toCharArray(), p = needle.toCharArray();
// Traverse through the haystack string
for (int i = 0; i < n - m + 1; i++) {
// Initialize matching pointers
int a = i, b = 0;
// Loop to check if the needle matches starting at the current location
while (b < m && s[a] == p[b]) {
// If the current character matches, move the pointers
a++;
b++;
}
// If b is equal to m, it means the needle is fully matched, return the current position i
if (b == m) return i;
}
// If the loop concludes without finding a match, return -1
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
/**
* Based on sliding window
*
* Time Complexity: O(m*n)
* Space Complexity: O(1)
* Note: n is the length of the haystack, m is the length of the needle
*/
public int strStr(String haystack, String needle) {
int m = needle.length();
// When needle is an empty string we should return 0
if (m == 0) {
return 0;
}
int n = haystack.length();
if (n < m) {
return -1;
}
int i = 0;
int j = 0;
while (i < n - m + 1) {
// Find the first matching letter
while (i < n && haystack.charAt(i) != needle.charAt(j)) {
i++;
}
if (i == n) { // No matching first letter found
return -1;
}
// Proceed to check if the subsequent characters match
i++;
j++;
while (i < n && j < m && haystack.charAt(i) == needle.charAt(j)) {
i++;
j++;
}
if (j == m) { // Match found
return i - j;
} else { // No match found
i -= j - 1;
j = 0;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// Method 1
class Solution {
public void getNext(int[] next, String s){
int j = -1;
next[0] = j;
for (int i = 1; i < s.length(); i++){
while(j >= 0 && s.charAt(i) != s.charAt(j+1)){
j=next[j];
}
if(s.charAt(i) == s.charAt(j+1)){
j++;
}
next[i] = j;
}
}
public int strStr(String haystack, String needle) {
if(needle.length()==0){
return 0;
}
int[] next = new int[needle.length()];
getNext(next, needle);
int j = -1;
for(int i = 0; i < haystack.length(); i++){
while(j>=0 && haystack.charAt(i) != needle.charAt(j+1)){
j = next[j];
}
if(haystack.charAt(i) == needle.charAt(j+1)){
j++;
}
if(j == needle.length()-1){
return (i-needle.length()+1);
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
// Prefix Table (without subtracting one) Java implementation
public int strStr(String haystack, String needle) {
if (needle.length() == 0) return 0;
int[] next = new int[needle.length()];
getNext(next, needle);
int j = 0;
for (int i = 0; i < haystack.length(); i++) {
while (j > 0 && needle.charAt(j) != haystack.charAt(i))
j = next[j - 1];
if (needle.charAt(j) == haystack.charAt(i))
j++;
if (j == needle.length())
return i - needle.length() + 1;
}
return -1;
}
private void getNext(int[] next, String s) {
int j = 0;
next[0] = 0;
for (int i = 1; i < s.length(); i++) {
while (j > 0 && s.charAt(j) != s.charAt(i))
j = next[j - 1];
if (s.charAt(j) == s.charAt(i))
j++;
next[i] = j;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Python3:
(Version 1) Prefix table (subtracting one)
class Solution:
def getNext(self, next, s):
j = -1
next[0] = j
for i in range(1, len(s)):
while j >= 0 and s[i] != s[j+1]:
j = next[j]
if s[i] == s[j+1]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if not needle:
return 0
next = [0] * len(needle)
self.getNext(next, needle)
j = -1
for i in range(len(haystack)):
while j >= 0 and haystack[i] != needle[j+1]:
j = next[j]
if haystack[i] == needle[j+1]:
j += 1
if j == len(needle) - 1:
return i - len(needle) + 1
return -1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(Version 2) Prefix table (not subtracting one)
class Solution:
def getNext(self, next: List[int], s: str) -> None:
j = 0
next[0] = 0
for i in range(1, len(s)):
while j > 0 and s[i] != s[j]:
j = next[j - 1]
if s[i] == s[j]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if len(needle) == 0:
return 0
next = [0] * len(needle)
self.getNext(next, needle)
j = 0
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j]:
j = next[j - 1]
if haystack[i] == needle[j]:
j += 1
if j == len(needle):
return i - len(needle) + 1
return -1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(Version 3) Brute-force method
class Solution(object):
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
m, n = len(haystack), len(needle)
for i in range(m):
if haystack[i:i+n] == needle:
return i
return -1
2
3
4
5
6
7
8
9
10
11
12
(Version 4) Using index
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
try:
return haystack.index(needle)
except ValueError:
return -1
2
3
4
5
6
(Version 5) Using find
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
return haystack.find(needle)
2
3
4
# Go:
// Method 1: Prefix table implementation with subtraction of 1
// getNext builds the next array for KMP
// params:
// next - prefix table array
// s - pattern string
func getNext(next []int, s string) {
j := -1 // j represents the length of the longest matching prefix
next[0] = j
for i := 1; i < len(s); i++ {
for j >= 0 && s[i] != s[j+1] {
j = next[j] // Backtrack to a shorter prefix match
}
if s[i] == s[j+1] {
j++
}
next[i] = j // next[i] is the length of the longest matching prefix before i
}
}
func strStr(haystack string, needle string) int {
if len(needle) == 0 {
return 0
}
next := make([]int, len(needle))
getNext(next, needle)
j := -1 // Start from the beginning of the pattern, next is initialized to -1
for i := 0; i < len(haystack); i++ {
for j >= 0 && haystack[i] != needle[j+1] {
j = next[j] // Find next match position
}
if haystack[i] == needle[j+1] {
j++
}
if j == len(needle)-1 { // j points to the end of the pattern
return i - len(needle) + 1
}
}
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// Method 2: Prefix table without subtraction of 1 or shifting
// getNext builds the next array for KMP
// params:
// next - prefix table array
// s - pattern string
func getNext(next []int, s string) {
j := 0
next[0] = 0
for i := 1; i < len(s); i++ {
for j > 0 && s[i] != s[j] {
j = next[j-1]
}
if s[i] == s[j] {
j++
}
next[i] = j
}
}
func strStr(haystack string, needle string) int {
n := len(needle)
if n == 0 {
return 0
}
j := 0
next := make([]int, n)
getNext(next, needle)
for i := 0; i < len(haystack); i++ {
for j > 0 && haystack[i] != needle[j] {
j = next[j-1] // Backtrack to previous position of j
}
if haystack[i] == needle[j] {
j++
}
if j == n {
return i - n + 1
}
}
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# JavaScript:
Prefix table with subtraction of 1
/**
* @param {string} haystack
* @param {string} needle
* @return {number}
*/
var strStr = function (haystack, needle) {
if (needle.length === 0)
return 0;
const getNext = (needle) => {
let next = [];
let j = -1;
next.push(j);
for (let i = 1; i < needle.length; ++i) {
while (j >= 0 && needle[i] !== needle[j + 1])
j = next[j];
if (needle[i] === needle[j + 1])
j++;
next.push(j);
}
return next;
}
let next = getNext(needle);
let j = -1;
for (let i = 0; i < haystack.length; ++i) {
while (j >= 0 && haystack[i] !== needle[j + 1])
j = next[j];
if (haystack[i] === needle[j + 1])
j++;
if (j === needle.length - 1)
return (i - needle.length + 1);
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Prefix table without subtraction of 1
/**
* @param {string} haystack
* @param {string} needle
* @return {number}
*/
var strStr = function (haystack, needle) {
if (needle.length === 0)
return 0;
const getNext = (needle) => {
let next = [];
let j = 0;
next.push(j);
for (let i = 1; i < needle.length; ++i) {
while (j > 0 && needle[i] !== needle[j])
j = next[j - 1];
if (needle[i] === needle[j])
j++;
next.push(j);
}
return next;
}
let next = getNext(needle);
let j = 0;
for (let i = 0; i < haystack.length; ++i) {
while (j > 0 && haystack[i] !== needle[j])
j = next[j - 1];
if (haystack[i] === needle[j])
j++;
if (j === needle.length)
return (i - needle.length + 1);
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# TypeScript:
Prefix table with subtraction of 1
function strStr(haystack: string, needle: string): number {
function getNext(str: string): number[] {
let next: number[] = [];
let j: number = -1;
next[0] = j;
for (let i = 1, length = str.length; i < length; i++) {
while (j >= 0 && str[i] !== str[j + 1]) {
j = next[j];
}
if (str[i] === str[j + 1]) {
j++;
}
next[i] = j;
}
return next;
}
if (needle.length === 0) return 0;
let next: number[] = getNext(needle);
let j: number = -1;
for (let i = 0, length = haystack.length; i < length; i++) {
while (j >= 0 && haystack[i] !== needle[j + 1]) {
j = next[j];
}
if (haystack[i] === needle[j + 1]) {
if (j === needle.length - 2) {
return i - j - 1;
}
j++;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Prefix table without subtraction of 1
// Without subtraction
function strStr(haystack: string, needle: string): number {
function getNext(str: string): number[] {
let next: number[] = [];
let j: number = 0;
next[0] = j;
for (let i = 1, length = str.length; i < length; i++) {
while (j > 0 && str[i] !== str[j]) {
j = next[j - 1];
}
if (str[i] === str[j]) {
j++;
}
next[i] = j;
}
return next;
}
if (needle.length === 0) return 0;
let next: number[] = getNext(needle);
let j: number = 0;
for (let i = 0, length = haystack.length; i < length; i++) {
while (j > 0 && haystack[i] !== needle[j]) {
j = next[j - 1];
}
if (haystack[i] === needle[j]) {
if (j === needle.length - 1) {
return i - j;
}
j++;
}
}
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Swift:
Prefix table with subtraction of 1
func strStr(_ haystack: String, _ needle: String) -> Int {
let s = Array(haystack), p = Array(needle)
guard p.count != 0 else { return 0 }
// 2 pointer
var j = -1
var next = [Int](repeating: -1, count: needle.count)
// KMP
getNext(&next, needle: p)
for i in 0 ..< s.count {
while j >= 0 && s[i] != p[j + 1] {
// Backtrack to a matching position
j = next[j]
}
if s[i] == p[j + 1] {
// Matching, move both pointers forward
j += 1
}
if j == (p.count - 1) {
// Matching substring found
return i - p.count + 1
}
}
return -1
}
// Subtract prefix table
func getNext(_ next: inout [Int], needle: [Character]) {
var j: Int = -1
next[0] = j
// i starts from the second character
for i in 1 ..< needle.count {
while j >= 0 && needle[i] != needle[j + 1] {
j = next[j]
}
if needle[i] == needle[j + 1] {
j += 1;
}
next[i] = j
}
print(next)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Right-shift prefix table
func strStr(_ haystack: String, _ needle: String) -> Int {
let s = Array(haystack), p = Array(needle)
guard p.count != 0 else { return 0 }
var j = 0
var next = [Int].init(repeating: 0, count: p.count)
getNext(&next, p)
for i in 0 ..< s.count {
while j > 0 && s[i] != p[j] {
j = next[j - 1]
}
if s[i] == p[j] {
j += 1
}
if j == p.count {
return i - p.count + 1
}
}
return -1
}
// Shift prefix table to the right
func getNext(_ next: inout [Int], _ needle: [Character]) {
guard needle.count > 1 else { return }
var j = 0
next[0] = j
for i in 1 ..< needle.count-1 {
while j > 0 && needle[i] != needle[j] {
j = next[j-1]
}
if needle[i] == needle[j] {
j += 1
}
next[i] = j
}
next.removeLast()
next.insert(-1, at: 0)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Prefix table without subtraction
func strStr(_ haystack: String, _ needle: String) -> Int {
let s = Array(haystack), p = Array(needle)
guard p.count != 0 else { return 0 }
var j = 0
var next = [Int](repeating: 0, count: needle.count)
// KMP
getNext(&next, needle: p)
for i in 0 ..< s.count {
while j > 0 && s[i] != p[j] {
j = next[j-1]
}
if s[i] == p[j] {
j += 1
}
if j == p.count {
return i - p.count + 1
}
}
return -1
}
//Prefix table
func getNext(_ next: inout [Int], needle: [Character]) {
var j = 0
next[0] = j
for i in 1 ..< needle.count {
while j>0 && needle[i] != needle[j] {
j = next[j-1]
}
if needle[i] == needle[j] {
j += 1
}
next[i] = j
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# PHP:
Prefix table with subtraction of 1
function strStr($haystack, $needle) {
if (strlen($needle) == 0) return 0;
$next= [];
$this->getNext($next,$needle);
$j = -1;
for ($i = 0;$i < strlen($haystack); $i++) { // Note i starts from 0
while($j >= 0 && $haystack[$i] != $needle[$j + 1]) {
$j = $next[$j];
}
if ($haystack[$i] == $needle[$j + 1]) {
$j++;
}
if ($j == (strlen($needle) - 1) ) {
return ($i - strlen($needle) + 1);
}
}
return -1;
}
function getNext(&$next, $s){
$j = -1;
$next[0] = $j;
for($i = 1; $i < strlen($s); $i++) { // Note i starts from 1
while ($j >= 0 && $s[$i] != $s[$j + 1]) {
$j = $next[$j];
}
if ($s[$i] == $s[$j + 1]) {
$j++;
}
$next[$i] = $j;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Prefix table without subtraction of 1
function strStr($haystack, $needle) {
if (strlen($needle) == 0) return 0;
$next= [];
$this->getNext($next,$needle);
$j = 0;
for ($i = 0;$i < strlen($haystack); $i++) { // Note i starts from 0
while($j > 0 && $haystack[$i] != $needle[$j]) {
$j = $next[$j-1];
}
if ($haystack[$i] == $needle[$j]) {
$j++;
}
if ($j == strlen($needle)) {
return ($i - strlen($needle) + 1);
}
}
return -1;
}
function getNext(&$next, $s){
$j = 0;
$next[0] = $j;
for($i = 1; $i < strlen($s); $i++) { // Note i starts from 1
while ($j > 0 && $s[$i] != $s[$j]) {
$j = $next[$j-1];
}
if ($s[$i] == $s[$j]) {
$j++;
}
$next[$i] = $j;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Rust:
Prefix table without subtraction of 1
impl Solution {
pub fn get_next(next: &mut Vec<usize>, s: &Vec<char>) {
let len = s.len();
let mut j = 0;
for i in 1..len {
while j > 0 && s[i] != s[j] {
j = next[j - 1];
}
if s[i] == s[j] {
j += 1;
}
next[i] = j;
}
}
pub fn str_str(haystack: String, needle: String) -> i32 {
let (haystack_len, needle_len) = (haystack.len(), needle.len());
if haystack_len < needle_len { return -1;}
let (haystack, needle) = (haystack.chars().collect::<Vec<char>>(), needle.chars().collect::<Vec<char>>());
let mut next: Vec<usize> = vec![0; haystack_len];
Self::get_next(&mut next, &needle);
let mut j = 0;
for i in 0..haystack_len {
while j > 0 && haystack[i] != needle[j] {
j = next[j - 1];
}
if haystack[i] == needle[j] {
j += 1;
}
if j == needle_len {
return (i - needle_len + 1) as i32;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Prefix table with subtraction of 1
impl Solution {
pub fn get_next(next_len: usize, s: &Vec<char>) -> Vec<i32> {
let mut next = vec![-1; next_len];
let mut j = -1;
for i in 1..s.len() {
while j >= 0 && s[(j + 1) as usize] != s[i] {
j = next[j as usize];
}
if s[i] == s[(j + 1) as usize] {
j += 1;
}
next[i] = j;
}
next
}
pub fn str_str(haystack: String, needle: String) -> i32 {
if haystack.len() < needle.len() {
return -1;
}
let (haystack_chars, needle_chars) = (
haystack.chars().collect::<Vec<char>>(),
needle.chars().collect::<Vec<char>>(),
);
let mut j = -1;
let next = Self::get_next(needle.len(), &needle_chars);
for (i, v) in haystack_chars.into_iter().enumerate() {
while j >= 0 && v != needle_chars[(j + 1) as usize] {
j = next[j as usize];
}
if v == needle_chars[(j + 1) as usize] {
j += 1;
}
if j == needle_chars.len() as i32 - 1 {
return (i - needle_chars.len() + 1) as i32;
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Prefix table without subtraction of 1
public int StrStr(string haystack, string needle)
{
if (string.IsNullOrEmpty(needle))
return 0;
if (needle.Length > haystack.Length || string.IsNullOrEmpty(haystack))
return -1;
return KMP(haystack, needle);
}
public int KMP(string haystack, string needle)
{
int[] next = GetNext(needle);
int i = 0, j = 0;
while (i < haystack.Length)
{
if (haystack[i] == needle[j])
{
i++;
j++;
}
if (j == needle.Length)
return i-j;
else if (i < haystack.Length && haystack[i] != needle[j])
if (j != 0)
{
j = next[j - 1];
}
else
{
i++;
}
}
return -1;
}
public int[] GetNext(string needle)
{
int[] next = new int[needle.Length];
next[0] = 0;
int i = 1, j = 0;
while (i < needle.Length)
{
if (needle[i] == needle[j])
{
next[i++] = ++j;
}
else
{
if (j == 0)
{
next[i++] = 0;
}
else
{
j = next[j - 1];
}
}
}
return next;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# C:
Prefix table with right-shift and subtraction of 1
int *build_next(char* needle, int len) {
int *next = (int *)malloc(len * sizeof(int));
assert(next); // Ensure successful allocation
// Initialize the next array
next[0] = -1; // next[0] set to -1, indicates no valid prefix match
if (len <= 1) { // Directly return if pattern length is less than or equal to 1
return next;
}
next[1] = 0; // next[1] set to 0, indicates no common prefix or suffix for the first character
// Construct next array: i starts from the third character of the pattern, j points to the current matching longest prefix length
int i = 2, j = 0;
while (i < len) {
if (needle[i - 1] == needle[j]) {
j++;
next[i] = j;
i++;
} else if (j > 0) {
// If mismatch and j > 0, backtrack to shorter matching prefix length
j = next[j];
} else {
next[i] = 0;
i++;
}
}
return next;
}
int strStr(char* haystack, char* needle) {
int needle_len = strlen(needle);
int haystack_len = strlen(haystack);
int *next = build_next(needle, needle_len);
int i = 0, j = 0; // i points to the current start of the main string, j points to the current matching position of the pattern
while (i <= haystack_len - needle_len) {
if (haystack[i + j] == needle[j]) {
j++;
if (j == needle_len) {
free(next);
next = NULL
return i;
}
} else {
i += j - next[j]; // Adjust main string start position
j = j > 0 ? next[j] : 0;
}
}
free(next);
next = NULL;
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
